Velocidade angular instantânea
Storyboard 
A velocidade angular média é definida levando em consideração o ângulo percorrido durante um intervalo de tempo, sem considerar as possíveis flutuações na velocidade angular.
Para determinar a velocidade angular em um instante específico, é necessário considerar um intervalo de tempo extremamente pequeno, de modo que a velocidade angular não tenha variações significativas nesse período.
Por essa razão, obtém-se a velocidade angular instantânea calculando a velocidade angular média no limite de um intervalo de tempo que tende a zero. Do ponto de vista matemático, isso equivale à derivada da posição em relação ao tempo e à inclinação da curva ângulo-tempo.
ID:(1447, 0)
Velocidade angular instantânea
Storyboard 
A velocidade angular média é definida levando em consideração o ângulo percorrido durante um intervalo de tempo, sem considerar as possíveis flutuações na velocidade angular. Para determinar a velocidade angular em um instante específico, é necessário considerar um intervalo de tempo extremamente pequeno, de modo que a velocidade angular não tenha variações significativas nesse período. Por essa razão, obtém-se a velocidade angular instantânea calculando a velocidade angular média no limite de um intervalo de tempo que tende a zero. Do ponto de vista matemático, isso equivale à derivada da posição em relação ao tempo e à inclinação da curva ângulo-tempo.
Variáveis
Cálculos
Cálculos
Equações
Se considerarmos o ngulo percorrido como la variação de ângulo ($\Delta\theta$) no tempo $t+\Delta t$ e em $t$:
$\Delta\theta = \theta(t+\Delta t)-\theta(t)$
e o tempo decorrido ($\Delta t$), ent o no limite de tempos infinitesimalmente curtos:
$\omega=\displaystyle\frac{\Delta\theta}{\Delta t}=\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}\rightarrow lim_{\Delta t\rightarrow 0}\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}=\displaystyle\frac{d\theta}{dt}$
Esta ltima express o corresponde derivada da fun o de ngulo $\theta(t)$, que por sua vez a inclina o da representa o gr fica dessa fun o no tempo.
Aqui est a vers o melhorada:
"Dado que la velocidade ($v$) com la velocidade angular instantânea ($\omega$) e o rádio ($r$), igual a
podemos calcular la velocidade (vector) ($\vec{v}$) usando o produto cruzado com o vetor do eixo, denotado por $\hat{n}$, e o vetor radial, denotado por $\hat{r}$:
$\hat{t} = \hat{n} \times \hat{r}$
Portanto, se definirmos
$\vec{v}=v\hat{t}$
,
$\vec{r}=r\hat{r}$
e
$\vec{\omega}=\omega\hat{n}$
,
ent o podemos expressar a velocidade como
$\vec{v}=v\hat{t}=v\hat{n}\times\hat{r}=r\omega\hat{n}\times\hat{r}=\vec{\omega}\times\vec{r}$
ou seja
Exemplos
Se tomarmos um tempo $t$ com um ngulo $\theta(t)$ e observarmos um ponto em um tempo futuro $t+\Delta t$ com um ngulo $\theta(t+\Delta t)$, podemos estimar a velocidade como o ngulo percorrido
$\theta(t+\Delta t)-\theta(t)$
no tempo $\Delta t$.
$\omega\sim\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}$
medida que o valor de $\Delta t$ reduzido, a velocidade angular assume o papel da tangente curva de posi o naquele tempo:
Isso generaliza o que j foi visto para o caso de velocidade angular constante.
Se observarmos que a velocidade angular $\omega$ igual ao ngulo $\Delta\theta$ multiplicado pelo tempo $\Delta t$, podemos afirmar que o deslocamento
$\Delta\theta = \omega\Delta t$
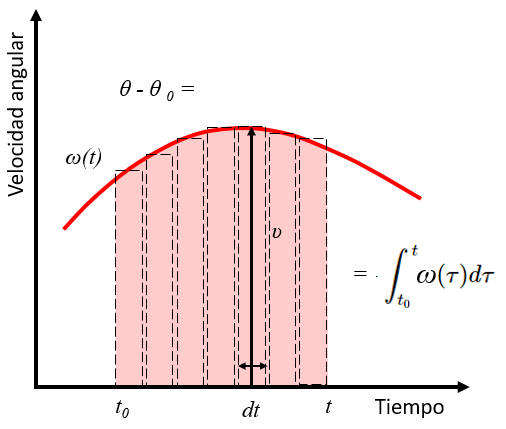
Uma vez que o produto $\omega\Delta t$ representa a rea sob a curva de velocidade angular em fun o do tempo, e essa rea tamb m igual ao deslocamento percorrido:
A integral de uma fun o corresponde rea sob a curva que define a fun o. Portanto, a integral da velocidade entre os tempos $t_0$ e $t$ corresponde ao ngulo percorrido entre a posi o inicial $\theta_0$ e $\theta$.
Isso pode ser expresso matematicamente como:
Essa rela o mostrada graficamente abaixo:
Essa f rmula til para calcular o ngulo percorrido por um objeto em situa es em que se conhece a fun o de velocidade. A integral da fun o de velocidade fornece uma medida do deslocamento total do objeto entre os dois tempos $t_0$ e $t$, o que pode ser usado para calcular o ngulo percorrido pelo objeto dividindo o deslocamento pelo raio do c rculo. Esse conceito especialmente til em aplica es de f sica e engenharia em que o movimento de rota o est envolvido.
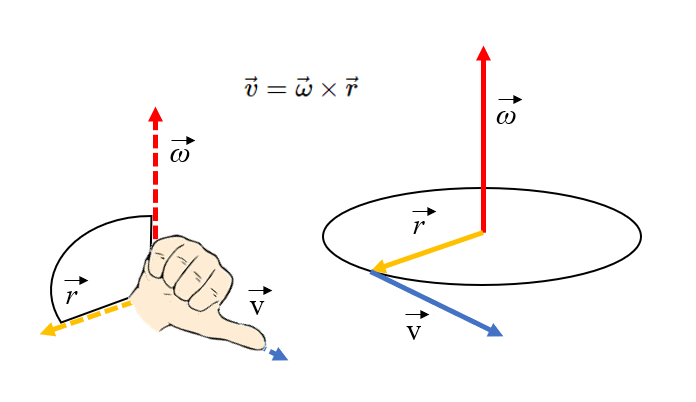
A orienta o da velocidade tangencial pode ser obtida usando a regra da m o direita. Se os dedos apontam em dire o ao eixo de rota o e s o curvados em dire o ao vetor de posi o (raio), o polegar apontar na dire o da velocidade tangencial:
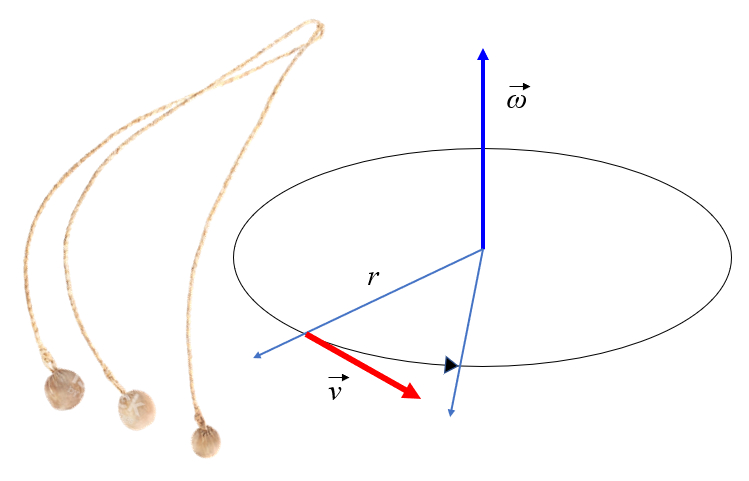
Se um objeto submetido a um modo de manter um raio constante, ele ir girar conforme indicado na figura. Ao observar a figura, notar -se que a massa realiza um movimento de transla o com uma velocidade tangencial que igual ao raio multiplicado pela velocidade angular:
No entanto, se o elemento que conecta o objeto ao eixo for cortado, o objeto continuar a se mover tangencialmente em linha reta.
A La velocidade angular média ($\bar{\omega}$) calculada a partir de uma variação de ângulo ($\Delta\theta$) e o tempo decorrido ($\Delta t$) atrav s da equa o
uma aproxima o do real la velocidade angular instantânea ($\omega$), que tende a distorcer-se medida que a velocidade angular flutua durante o intervalo de tempo. Portanto, introduzido o conceito de la velocidade angular instantânea ($\omega$) determinado em um tempo muito pequeno. Neste caso, falamos de um intervalo de tempo infinitesimalmente pequeno.
que corresponde derivada do ngulo.
Como o tempo ($t$) a derivada de o ângulo ($\theta$) em rela o a la velocidade angular instantânea ($\omega$), ou seja,
a integra o de o tempo ($t$) entre o tempo inicial ($t_0$) e o tempo ($t$) corresponder ao ngulo percorrido entre o ângulo inicial ($\theta_0$) e o ângulo ($\theta$), como demonstrado em
La velocidade angular instantânea ($\omega$) definido como um vetor cuja dire o coincide com o eixo de rota o. Dado que a rota o o rádio ($r$) e la velocidade angular instantânea ($\omega$) s o perpendiculares a la velocidade ($v$), pode ser expressa como o produto vetorial entre la velocidade angular instantânea ($\omega$) e a rota o o rádio ($r$):
la velocidade ($v$) pode ser escrita em forma vetorial como la velocidade (vector) ($\vec{v}$), resultante do produto cruz entre la velocidade angular ($\vec{\omega}$) e la raio (vetor) ($\vec{r}$):
Em geral, la velocidade angular instantânea ($\omega$) deve ser entendido como uma entidade tridimensional, ou seja, um vetor la velocidade angular ($\vec{\omega}$). Cada componente pode ser definida como a derivada de o ângulo ($\theta$) em rela o a o tempo ($t$):
Assim, pode-se express -lo com a derivada em rela o a o tempo ($t$) de o ângulo (vetor) ($\vec{\theta}$) como la velocidade angular ($\vec{\omega}$):
ID:(1447, 0)