Aceleración angular constante, dos etapas
Storyboard 
En el caso de un movimiento acelerado angular en dos etapas, en el momento en que se pasa de la primera a la segunda aceleración angular, la velocidad angular final de la primera etapa se convierte en la velocidad angular inicial de la segunda. Lo mismo ocurre con el ángulo, donde el ángulo final de la primera etapa es igual al ángulo inicial de la segunda etapa.A diferencia del modelo de dos velocidades angulares, este modelo no presenta problemas de discontinuidad, excepto que la aceleración angular puede cambiar de forma abrupta, lo cual es técnicamente posible aunque muchas veces no tan realista.
ID:(1409, 0)
Movimiento en dos etapas
Descripción 
En un escenario de movimiento en dos fases, inicialmente el objeto ajusta su velocidad por la diferencia de la variación de velocidades angulares en la primera etapa ($\Delta\omega_1$) durante un período de el tiempo transcurrido en la primera etapa ($\Delta t_1$), experimentando una aceleración de la aceleración angular durante la primera etapa ($\alpha_1$).
| $ \alpha_1 \equiv \displaystyle\frac{ \Delta\omega_1 }{ \Delta t_1 }$ |
En la segunda fase, el objeto continua modificando su velocidad por la variación de velocidades angulares en la segunda etapa ($\Delta\omega_2$) a lo largo de un intervalo de tiempo el tiempo transcurrido en la segunda etapa ($\Delta t_2$), con una aceleración de la aceleración angular durante la segunda etapa ($\alpha_2$).
| $ \alpha_2 \equiv \displaystyle\frac{ \Delta\omega_2 }{ \Delta t_2 }$ |
Al visualizar esto gráficamente, se obtiene un diagrama de velocidad contra tiempo como el que se muestra a continuación:
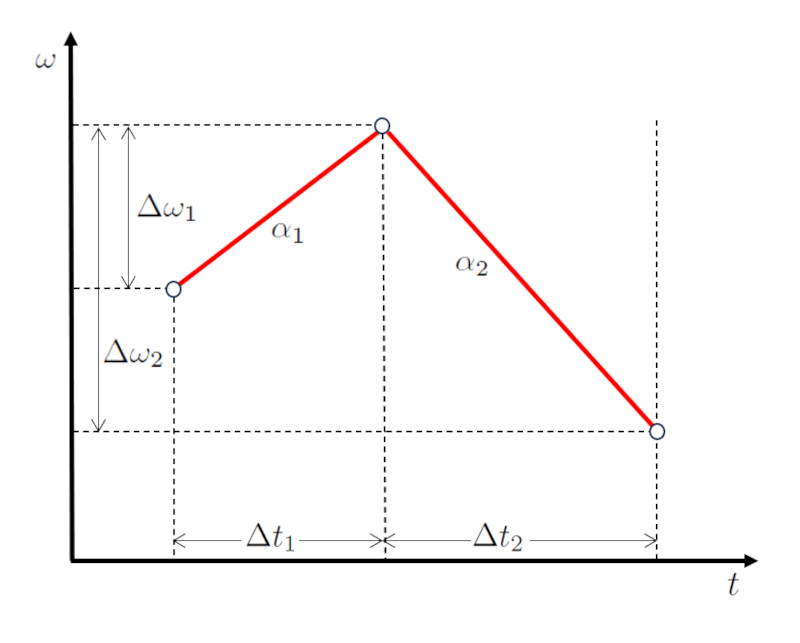
Es importante notar que los intervalos de tiempo el tiempo transcurrido en la primera etapa ($\Delta t_1$) y el tiempo transcurrido en la segunda etapa ($\Delta t_2$) son consecutivos, así como las diferencias en la velocidad la variación de velocidades angulares en la primera etapa ($\Delta\omega_1$) y la variación de velocidades angulares en la segunda etapa ($\Delta\omega_2$).
ID:(12521, 0)
Velocidad angular en un movimiento en dos etapas
Descripción 
En el análisis de un movimiento segmentado en dos etapas, la primera fase se caracteriza mediante una función lineal que incorpora los puntos el tiempo inicial ($t_0$), el tiempo final primera e inició segunda etapa ($t_1$), la velocidad angular inicial ($\omega_0$) y la velocidad ángular final primera e inicio segunda etapa ($\omega_1$). Esta se expresa a través de una recta con una pendiente de la aceleración angular durante la primera etapa ($\alpha_1$), cuya relación matemática se especifica en la siguiente ecuación:
| $ \omega_1 = \omega_0 + \alpha_1 ( t_1 - t_0 )$ |
En la transición a la segunda etapa, la cual está definida por los puntos la velocidad ángular final primera e inicio segunda etapa ($\omega_1$), la velocidad ángular final de la segunda etapa ($\omega_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), se adopta una nueva función lineal con una pendiente de la aceleración angular durante la segunda etapa ($\alpha_2$). Esta relación es delineada por la segunda ecuación presentada:
| $ \omega_2 = \omega_1 + \alpha_2 ( t_2 - t_1 )$ |
La representación gráfica de estas relaciones lineales se ilustra a continuación, proporcionando una visualización clara de cómo varía la pendiente entre las dos etapas:
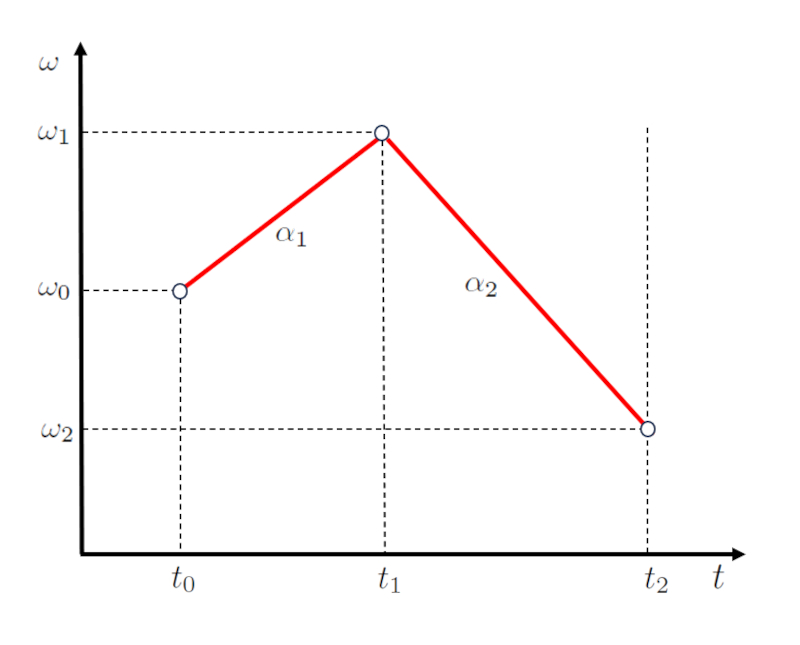
ID:(12522, 0)
Ángulo en un movimiento en dos etapas
Descripción 
En un escenario de movimiento dividido en dos etapas, el ángulo al final de la primera etapa es el mismo que el ángulo al inicio de la segunda etapa, designado como el ángulo final primera e inició segunda etapa ($\theta_1$).
Asimismo, el momento en que finaliza la primera etapa coincide con el inicio de la segunda etapa, marcado por el tiempo final primera e inició segunda etapa ($t_1$).
Dado que el movimiento está definido por la aceleración angular experimentada, la velocidad angular al final de la primera etapa debe ser igual a la velocidad angular al inicio de la segunda etapa, indicada por la velocidad ángular final primera e inicio segunda etapa ($\omega_1$).
En el contexto de una aceleración angular constante, el ángulo en el ángulo final primera e inició segunda etapa ($\theta_1$) se determina por las variables el ángulo inicial ($\theta_0$), la velocidad angular inicial ($\omega_0$), la aceleración angular durante la primera etapa ($\alpha_1$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo inicial ($t_0$), como se muestra en la siguiente ecuación:
| $ \theta_1 = \theta_0 + \omega_0 ( t_1 - t_0 )+\displaystyle\frac{1}{2} \alpha_1 ( t_1 - t_0 )^2$ |
En la segunda etapa, el ángulo en la ángulo final segunda etapa ($\theta_2$) se calcula en función de el ángulo final primera e inició segunda etapa ($\theta_1$), la velocidad ángular final primera e inicio segunda etapa ($\omega_1$), la aceleración angular durante la segunda etapa ($\alpha_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), conforme a:
| $ \theta_2 = \theta_1 + \omega_1 ( t_2 - t_1 )+\displaystyle\frac{1}{2} \alpha_2 ( t_2 - t_1 )^2$ |
La representación gráfica de estas relaciones se ilustra a continuación:
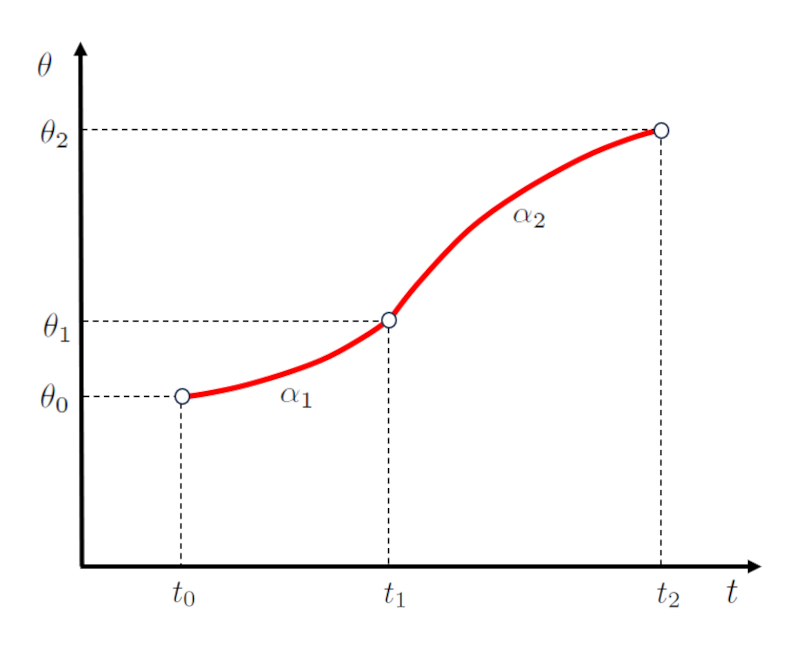
ID:(12520, 0)
Aceleración angular constante, dos etapas
Modelo 
En el caso de un movimiento acelerado angular en dos etapas, en el momento en que se pasa de la primera a la segunda aceleración angular, la velocidad angular final de la primera etapa se convierte en la velocidad angular inicial de la segunda. Lo mismo ocurre con el ángulo, donde el ángulo final de la primera etapa es igual al ángulo inicial de la segunda etapa. A diferencia del modelo de dos velocidades angulares, este modelo no presenta problemas de discontinuidad, excepto que la aceleración angular puede cambiar de forma abrupta, lo cual es técnicamente posible aunque muchas veces no tan realista.
Variables
Cálculos
Cálculos
Ecuaciones
La aceleraci n angular media se define como la proporci n del ngulo recorrido
| $ \Delta\omega = \omega_2 - \omega_1 $ |
y el tiempo transcurrido
| $ \Delta t \equiv t - t_0 $ |
Esta relaci n entre ambos se establece como la aceleraci n angular media
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
durante dicho intervalo de tiempo.
(ID 3234)
La aceleraci n angular media se define como la proporci n del ngulo recorrido
| $ \Delta\omega = \omega_2 - \omega_1 $ |
y el tiempo transcurrido
| $ \Delta t \equiv t - t_0 $ |
Esta relaci n entre ambos se establece como la aceleraci n angular media
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
durante dicho intervalo de tiempo.
(ID 3234)
Dado que la aceleración media ($\bar{a}$) es igual a la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$) seg n
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
y la aceleración angular media ($\bar{\alpha}$) es igual a la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$) conforme a
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
se deduce que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Si asumimos que la aceleración angular media ($\bar{\alpha}$) es igual a la aceleración angular constante ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
y suponiendo que la aceleración media ($\bar{a}$) es igual a la aceleración constante ($a_0$)
| $ a_0 = \bar{a} $ |
entonces se obtiene la siguiente ecuaci n:
| $ a = r \alpha $ |
(ID 3236)
Dado que la aceleración media ($\bar{a}$) es igual a la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$) seg n
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
y la aceleración angular media ($\bar{\alpha}$) es igual a la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$) conforme a
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
se deduce que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Si asumimos que la aceleración angular media ($\bar{\alpha}$) es igual a la aceleración angular constante ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
y suponiendo que la aceleración media ($\bar{a}$) es igual a la aceleración constante ($a_0$)
| $ a_0 = \bar{a} $ |
entonces se obtiene la siguiente ecuaci n:
| $ a = r \alpha $ |
(ID 3236)
Si suponemos que la aceleración angular media ($\bar{\alpha}$) es constante, equivalente a la aceleración angular constante ($\alpha_0$), entonces se aplica la siguiente ecuaci n:
| $ \bar{\alpha} = \alpha_0 $ |
Por lo tanto, al considerar la diferencia de velocidades angulares ($\Delta\omega$) junto con la velocidad angular ($\omega$) y la velocidad angular inicial ($\omega_0$):
| $ \Delta\omega = \omega_2 - \omega_1 $ |
y el tiempo transcurrido ($\Delta t$) en relaci n con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
la ecuaci n para la aceleración angular media ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
puede expresarse como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Despejando esta ltima, obtenemos:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
Si suponemos que la aceleración angular media ($\bar{\alpha}$) es constante, equivalente a la aceleración angular constante ($\alpha_0$), entonces se aplica la siguiente ecuaci n:
| $ \bar{\alpha} = \alpha_0 $ |
Por lo tanto, al considerar la diferencia de velocidades angulares ($\Delta\omega$) junto con la velocidad angular ($\omega$) y la velocidad angular inicial ($\omega_0$):
| $ \Delta\omega = \omega_2 - \omega_1 $ |
y el tiempo transcurrido ($\Delta t$) en relaci n con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
la ecuaci n para la aceleración angular media ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
puede expresarse como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Despejando esta ltima, obtenemos:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
En el caso de la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) en funci n de el tiempo ($t$) sigue una relaci n lineal con el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) de la forma:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Dado que el ngulo recorrido es igual al rea bajo la curva de velocidad angular-tiempo, en este caso se puede sumar la contribuci n del rect ngulo:
$\omega_0(t-t_0)$
y el tri ngulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Esto nos lleva a la expresi n para el ángulo ($\theta$) y el ángulo inicial ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
En el caso de la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) en funci n de el tiempo ($t$) sigue una relaci n lineal con el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) de la forma:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Dado que el ngulo recorrido es igual al rea bajo la curva de velocidad angular-tiempo, en este caso se puede sumar la contribuci n del rect ngulo:
$\omega_0(t-t_0)$
y el tri ngulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Esto nos lleva a la expresi n para el ángulo ($\theta$) y el ángulo inicial ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
Si resolvemos la ecuaci n de la velocidad angular ($\omega$) en t rminos de tiempo, que incluye las variables la velocidad angular inicial ($\omega_0$), el tiempo ($t$), el tiempo inicial ($t_0$) y la aceleración angular constante ($\alpha_0$):
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
obtenemos la siguiente expresi n para el tiempo:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Esta soluci n puede ser sustituida en la ecuaci n para calcular el ángulo ($\theta$) utilizando el ángulo inicial ($\theta_0$) de la siguiente manera:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Lo que resulta en la siguiente ecuaci n:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
(ID 4386)
Si resolvemos la ecuaci n de la velocidad angular ($\omega$) en t rminos de tiempo, que incluye las variables la velocidad angular inicial ($\omega_0$), el tiempo ($t$), el tiempo inicial ($t_0$) y la aceleración angular constante ($\alpha_0$):
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
obtenemos la siguiente expresi n para el tiempo:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Esta soluci n puede ser sustituida en la ecuaci n para calcular el ángulo ($\theta$) utilizando el ángulo inicial ($\theta_0$) de la siguiente manera:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Lo que resulta en la siguiente ecuaci n:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
(ID 4386)
Ejemplos
(ID 15413)
En un escenario de movimiento en dos fases, inicialmente el objeto ajusta su velocidad por la diferencia de la variación de velocidades angulares en la primera etapa ($\Delta\omega_1$) durante un per odo de el tiempo transcurrido en la primera etapa ($\Delta t_1$), experimentando una aceleraci n de la aceleración angular durante la primera etapa ($\alpha_1$).
| $ \alpha_1 \equiv \displaystyle\frac{ \Delta\omega_1 }{ \Delta t_1 }$ |
En la segunda fase, el objeto continua modificando su velocidad por la variación de velocidades angulares en la segunda etapa ($\Delta\omega_2$) a lo largo de un intervalo de tiempo el tiempo transcurrido en la segunda etapa ($\Delta t_2$), con una aceleraci n de la aceleración angular durante la segunda etapa ($\alpha_2$).
| $ \alpha_2 \equiv \displaystyle\frac{ \Delta\omega_2 }{ \Delta t_2 }$ |
Al visualizar esto gr ficamente, se obtiene un diagrama de velocidad contra tiempo como el que se muestra a continuaci n:

Es importante notar que los intervalos de tiempo el tiempo transcurrido en la primera etapa ($\Delta t_1$) y el tiempo transcurrido en la segunda etapa ($\Delta t_2$) son consecutivos, as como las diferencias en la velocidad la variación de velocidades angulares en la primera etapa ($\Delta\omega_1$) y la variación de velocidades angulares en la segunda etapa ($\Delta\omega_2$).
(ID 12521)
En el an lisis de un movimiento segmentado en dos etapas, la primera fase se caracteriza mediante una funci n lineal que incorpora los puntos el tiempo inicial ($t_0$), el tiempo final primera e inició segunda etapa ($t_1$), la velocidad angular inicial ($\omega_0$) y la velocidad ángular final primera e inicio segunda etapa ($\omega_1$). Esta se expresa a trav s de una recta con una pendiente de la aceleración angular durante la primera etapa ($\alpha_1$), cuya relaci n matem tica se especifica en la siguiente ecuaci n:
| $ \omega_1 = \omega_0 + \alpha_1 ( t_1 - t_0 )$ |
En la transici n a la segunda etapa, la cual est definida por los puntos la velocidad ángular final primera e inicio segunda etapa ($\omega_1$), la velocidad ángular final de la segunda etapa ($\omega_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), se adopta una nueva funci n lineal con una pendiente de la aceleración angular durante la segunda etapa ($\alpha_2$). Esta relaci n es delineada por la segunda ecuaci n presentada:
| $ \omega_2 = \omega_1 + \alpha_2 ( t_2 - t_1 )$ |
La representaci n gr fica de estas relaciones lineales se ilustra a continuaci n, proporcionando una visualizaci n clara de c mo var a la pendiente entre las dos etapas:

(ID 12522)
En un escenario de movimiento dividido en dos etapas, el ngulo al final de la primera etapa es el mismo que el ngulo al inicio de la segunda etapa, designado como el ángulo final primera e inició segunda etapa ($\theta_1$).
Asimismo, el momento en que finaliza la primera etapa coincide con el inicio de la segunda etapa, marcado por el tiempo final primera e inició segunda etapa ($t_1$).
Dado que el movimiento est definido por la aceleraci n angular experimentada, la velocidad angular al final de la primera etapa debe ser igual a la velocidad angular al inicio de la segunda etapa, indicada por la velocidad ángular final primera e inicio segunda etapa ($\omega_1$).
En el contexto de una aceleraci n angular constante, el ngulo en el ángulo final primera e inició segunda etapa ($\theta_1$) se determina por las variables el ángulo inicial ($\theta_0$), la velocidad angular inicial ($\omega_0$), la aceleración angular durante la primera etapa ($\alpha_1$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo inicial ($t_0$), como se muestra en la siguiente ecuaci n:
| $ \theta_1 = \theta_0 + \omega_0 ( t_1 - t_0 )+\displaystyle\frac{1}{2} \alpha_1 ( t_1 - t_0 )^2$ |
En la segunda etapa, el ngulo en la ángulo final segunda etapa ($\theta_2$) se calcula en funci n de el ángulo final primera e inició segunda etapa ($\theta_1$), la velocidad ángular final primera e inicio segunda etapa ($\omega_1$), la aceleración angular durante la segunda etapa ($\alpha_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), conforme a:
| $ \theta_2 = \theta_1 + \omega_1 ( t_2 - t_1 )+\displaystyle\frac{1}{2} \alpha_2 ( t_2 - t_1 )^2$ |
La representaci n gr fica de estas relaciones se ilustra a continuaci n:

(ID 12520)
(ID 15424)
ID:(1409, 0)
