Utilizador:


Planejar
Storyboard

Se o objeto (avião/ave) mantiver um ângulo de ataque ligeiramente negativo, pode fazer com que parte da força de sustentação contribua para impulsionar e contrariar a resistência. Desde que a força de sustentação restante não seja muito inferior à força da gravidade, o objeto pode permanecer no ar por um longo período. Isso pode ser chamado de um descente controlada extremamente lenta ou planagem.

>Modelo

ID:(466, 0)


Mecanismos
Conceito


ID:(15177, 0)


Planejar
Descrição

Uma técnica de voo é conhecida como planar. Nesta técnica, as asas são usadas tanto para propulsão quanto para se manter no ar. Para alcançar isso, é essencial ajustar o ângulo de ataque da asa de forma que a força de sustentação compense a força gravitacional. Como resultado, o planar se torna uma descida controlada, na qual a descida é aproveitada para gerar sustentação e, assim, reduzir a velocidade de maneira controlada.

ID:(1171, 0)


Forças ao voar
Descrição

A chave para planar é inclinar a aeronave ou ave para a frente, ou seja, ter um ângulo negativo representado por ERROR:6121,0. Com esse ângulo negativo, o vetor la força de elevação ($F_L$) aponta para cima e para frente em vez de para trás. Isso resulta em uma força de tração em vez de la força de resistência ($F_W$), impulsionando a aeronave ou ave e gerando velocidade, o que, por sua vez, cria a sustentação necessária.



Esse mecanismo permite o voo, mas é essencial entender que é essencialmente uma descida lenta e controlada, uma vez que não se alcança um uma força de elevação ($F_L$) vertical que compense completamente o próprio peso. Portanto, é necessário levar a planadora a altas altitudes ou permitir que a ave ganhe altura inicialmente por meio de sua própria propulsão. Em seguida, ambos procuram correntes ascendentes que lhes permitem planar dentro de uma corrente ascendente mais forte do que a velocidade de descida da planadora. Dessa forma, eles podem permanecer em voo por longos períodos sem a necessidade de aterrissar.

ID:(7044, 0)


Ângulo de deslizamento
Descrição

Da mesma forma que o aceleração máxima ($\alpha$) é definido como o ângulo entre a linha central da asa e o horizonte, seu equivalente negativo pode ser definido como o ângulo de deslizamento ($\phi$).

Planador Jonker JS3 Rapture (Air Cargo Week)

ID:(7047, 0)


Forças em deslizamento
Descrição

No caso das forças, temos as seguintes ações:

• la força de elevação ($F_L$) age perpendicularmente ao eixo da aeronave ou ave.
• la força de resistência ($F_W$) age ao longo do eixo da aeronave ou ave.
• la força gravitacional ($F_g$) ($mg$) age verticalmente.

Essas três forças são representadas no centro do diagrama:

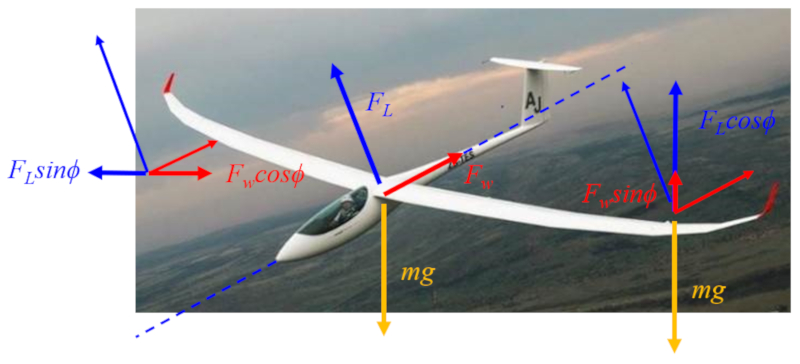
Planador Jonker JS3 Rapture (Air Cargo Week)

No lado esquerdo, pode-se observar a componente horizontal, onde a sustentação contraria o arrasto, atuando como impulso.No lado direito, são visíveis as componentes verticais, onde ambas as forças aerodinâmicas (sustentação e arrasto) se opõem ao peso que age sobre o centro de massa.Embora as forças se anulem entre si, o planador desce porque sua direção de voo é determinada pelo ângulo de planagem.

ID:(7046, 0)


Força de arrasto deslizante
Conceito

Se considerarmos la força de elevação ($F_L$), la força de resistência ($F_W$), la massa corporal ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$), a força durante o planeio na direção vertical é:

$ F_L \cos \phi + F_w \sin \phi = m g $



e na direção horizontal é:

$ F_L \sin \phi = F_w \cos \phi $



Isso nos permite eliminar la força de elevação ($F_L$), resultando em:

$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$



la força de resistência ($F_W$) deve ser:

$ F_W = m g \sin \phi $

ID:(15769, 0)


Força de elevação deslizante
Conceito

Se considerarmos la força de elevação ($F_L$), la força de resistência ($F_W$), la massa corporal ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$), a força durante o planeio na direção vertical é:

$ F_L \cos \phi + F_w \sin \phi = m g $



e na direção horizontal é:

$ F_L \sin \phi = F_w \cos \phi $



Isso nos permite eliminar la força de resistência ($F_W$), resultando em:

$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$



Portanto, la força de elevação ($F_L$) é:

$ F_L = m g \cos\phi $

ID:(15770, 0)


Ângulo de deslizamento
Conceito

Vamos considerar la força de elevação ($F_L$), la força de resistência ($F_W$), la massa corporal ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$). Com essas forças, a força de sustentação é calculada da seguinte forma:

$ F_L = m g \cos\phi $



e a força de arrasto como:

$ F_W = m g \sin \phi $



Podemos determinar o ângulo de deslizamento ($\phi$) dividindo la força de elevação ($F_L$) por la força de resistência ($F_W$), resultando em:

$\tan\phi=\displaystyle\frac{F_W}{F_L}$



Onde la força de resistência ($F_W$) é calculado usando a seguinte equação:

$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$



com o perfil total do objeto ($S_p$) e o coeficiente de resistência ($C_W$). Da mesma forma, la força de elevação ($F_L$) é calculado da seguinte forma:

$ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$



com la superfície que gera sustentação ($S_w$) e o coeficiente de elevação ($C_L$).

Com ambas as forças, podemos determinar o ângulo de ataque necessário para o planador da seguinte forma:

$ \tan \phi =\displaystyle\frac{ S_p C_w }{ S_w C_L }$

ID:(15771, 0)


Modelo
Conceito


ID:(15190, 0)


Planejar
Modelo

Se o objeto (avião/ave) mantiver um ângulo de ataque ligeiramente negativo, pode fazer com que parte da força de sustentação contribua para impulsionar e contrariar a resistência. Desde que a força de sustentação restante não seja muito inferior à força da gravidade, o objeto pode permanecer no ar por um longo período. Isso pode ser chamado de um descente controlada extremamente lenta ou planagem.

Variáveis
Símbolo
Texto
Variáve
Valor
Unidades
Calcular
Valeur MKS
Unidades MKS
$\phi$
phi
Ângulo de deslizamento
rad
$C_L$
C_L
Coeficiente de elevação
-
$C_W$
C_W
Coeficiente de resistência
-
$\rho$
rho
Densidade
kg/m^3
$F_L$
F_L
Força de elevação
N
$F_W$
F_W
Força de resistência
N
$m$
m
Massa corporal
kg
$S_p$
S_p
Perfil total do objeto
m^2
$S_w$
S_w
Superfície que gera sustentação
m^2
$v$
v
Velocidade em relação ao meio
m/s

Cálculos

Primeiro, selecione a equação:   para ,  depois, selecione a variável:   para 
Símbolo
Equação
Resolvido
Traduzido

Cálculos

Símbolo
Equação
Resolvido
Traduzido

 Variáve   Dado   Calcular   Objetivo :   Equação   A ser usado


Equações

La força de elevação ($F_L$), juntamente com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$), encontra-se em

$ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$



Se considerarmos la superfície que gera sustentação ($S_w$), definido por la envergadura das asas ($L$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$),

$ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$



e para o coeficiente de elevação ($C_L$), definido como

$ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$



obtemos

$ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$

(ID 4417)

De maneira semelhante forma como a equa o para la força de elevação ($F_L$) foi obtida utilizando la densidade ($\rho$), o coeficiente de elevação ($C_L$), la superfície que gera sustentação ($S_w$) e la velocidade em relação ao meio ($v$)

$ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$



nesta analogia, o que corresponde a la superfície que gera sustentação ($S_w$) ser equivalente a o perfil total do objeto ($S_p$) e o coeficiente de elevação ($C_L$) a o coeficiente de resistência ($C_W$), resultando no c lculo de la força de resistência ($F_W$):

$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$

O coeficiente de arrasto medido e, em fluxos turbulentos sobre corpos aerodin micos, geralmente se obt m valores em torno de 0.4.

(ID 4418)

Se considerarmos la força de elevação ($F_L$), la força de resistência ($F_W$), la massa corporal ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$), a for a durante o planeio na dire o vertical :

$ F_L \cos \phi + F_w \sin \phi = m g $



e na dire o horizontal :

$ F_L \sin \phi = F_w \cos \phi $



Isso nos permite eliminar la força de resistência ($F_W$), resultando em:

$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$



Portanto, la força de elevação ($F_L$) :

$ F_L = m g \cos\phi $

(ID 4421)

Se considerarmos la força de elevação ($F_L$), la força de resistência ($F_W$), la massa corporal ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$), a for a durante o planeio na dire o vertical :

$ F_L \cos \phi + F_w \sin \phi = m g $



e na dire o horizontal :

$ F_L \sin \phi = F_w \cos \phi $



Isso nos permite eliminar la força de elevação ($F_L$), resultando em:

$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$



la força de resistência ($F_W$) deve ser:

$ F_W = m g \sin \phi $

(ID 4422)

Vamos considerar la força de elevação ($F_L$), la força de resistência ($F_W$), la massa corporal ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$). Com essas for as, a for a de sustenta o calculada da seguinte forma:

$ F_L = m g \cos\phi $



e a for a de arrasto como:

$ F_W = m g \sin \phi $



Podemos determinar o ângulo de deslizamento ($\phi$) dividindo la força de elevação ($F_L$) por la força de resistência ($F_W$), resultando em:

$\tan\phi=\displaystyle\frac{F_W}{F_L}$



Onde la força de resistência ($F_W$) calculado usando a seguinte equa o:

$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$



com o perfil total do objeto ($S_p$) e o coeficiente de resistência ($C_W$). Da mesma forma, la força de elevação ($F_L$) calculado da seguinte forma:

$ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$



com la superfície que gera sustentação ($S_w$) e o coeficiente de elevação ($C_L$).

Com ambas as for as, podemos determinar o ngulo de ataque necess rio para o planador da seguinte forma:

$ \tan \phi =\displaystyle\frac{ S_p C_w }{ S_w C_L }$

(ID 4423)

Exemplos


(ID 15177)

Uma t cnica de voo conhecida como planar. Nesta t cnica, as asas s o usadas tanto para propuls o quanto para se manter no ar. Para alcan ar isso, essencial ajustar o ngulo de ataque da asa de forma que a for a de sustenta o compense a for a gravitacional. Como resultado, o planar se torna uma descida controlada, na qual a descida aproveitada para gerar sustenta o e, assim, reduzir a velocidade de maneira controlada.

(ID 1171)

A chave para planar inclinar a aeronave ou ave para a frente, ou seja, ter um ngulo negativo representado por ERROR:6121,0. Com esse ngulo negativo, o vetor la força de elevação ($F_L$) aponta para cima e para frente em vez de para tr s. Isso resulta em uma for a de tra o em vez de la força de resistência ($F_W$), impulsionando a aeronave ou ave e gerando velocidade, o que, por sua vez, cria a sustenta o necess ria.



Esse mecanismo permite o voo, mas essencial entender que essencialmente uma descida lenta e controlada, uma vez que n o se alcan a um uma força de elevação ($F_L$) vertical que compense completamente o pr prio peso. Portanto, necess rio levar a planadora a altas altitudes ou permitir que a ave ganhe altura inicialmente por meio de sua pr pria propuls o. Em seguida, ambos procuram correntes ascendentes que lhes permitem planar dentro de uma corrente ascendente mais forte do que a velocidade de descida da planadora. Dessa forma, eles podem permanecer em voo por longos per odos sem a necessidade de aterrissar.

(ID 7044)

Da mesma forma que o aceleração máxima ($\alpha$) definido como o ngulo entre a linha central da asa e o horizonte, seu equivalente negativo pode ser definido como o ângulo de deslizamento ($\phi$).

Planador Jonker JS3 Rapture (Air Cargo Week)

(ID 7047)

No caso das for as, temos as seguintes a es:

• la força de elevação ($F_L$) age perpendicularmente ao eixo da aeronave ou ave.
• la força de resistência ($F_W$) age ao longo do eixo da aeronave ou ave.
• la força gravitacional ($F_g$) ($mg$) age verticalmente.

Essas tr s for as s o representadas no centro do diagrama:

Planador Jonker JS3 Rapture (Air Cargo Week)

No lado esquerdo, pode-se observar a componente horizontal, onde a sustenta o contraria o arrasto, atuando como impulso.No lado direito, s o vis veis as componentes verticais, onde ambas as for as aerodin micas (sustenta o e arrasto) se op em ao peso que age sobre o centro de massa.Embora as for as se anulem entre si, o planador desce porque sua dire o de voo determinada pelo ngulo de planagem.

(ID 7046)

Se considerarmos la força de elevação ($F_L$), la força de resistência ($F_W$), la massa corporal ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$), a for a durante o planeio na dire o vertical :

$ F_L \cos \phi + F_w \sin \phi = m g $



e na dire o horizontal :

$ F_L \sin \phi = F_w \cos \phi $



Isso nos permite eliminar la força de elevação ($F_L$), resultando em:

$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$



la força de resistência ($F_W$) deve ser:

$ F_W = m g \sin \phi $

(ID 15769)

Se considerarmos la força de elevação ($F_L$), la força de resistência ($F_W$), la massa corporal ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$), a for a durante o planeio na dire o vertical :

$ F_L \cos \phi + F_w \sin \phi = m g $



e na dire o horizontal :

$ F_L \sin \phi = F_w \cos \phi $



Isso nos permite eliminar la força de resistência ($F_W$), resultando em:

$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$



Portanto, la força de elevação ($F_L$) :

$ F_L = m g \cos\phi $

(ID 15770)

Vamos considerar la força de elevação ($F_L$), la força de resistência ($F_W$), la massa corporal ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$). Com essas for as, a for a de sustenta o calculada da seguinte forma:

$ F_L = m g \cos\phi $



e a for a de arrasto como:

$ F_W = m g \sin \phi $



Podemos determinar o ângulo de deslizamento ($\phi$) dividindo la força de elevação ($F_L$) por la força de resistência ($F_W$), resultando em:

$\tan\phi=\displaystyle\frac{F_W}{F_L}$



Onde la força de resistência ($F_W$) calculado usando a seguinte equa o:

$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$



com o perfil total do objeto ($S_p$) e o coeficiente de resistência ($C_W$). Da mesma forma, la força de elevação ($F_L$) calculado da seguinte forma:

$ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$



com la superfície que gera sustentação ($S_w$) e o coeficiente de elevação ($C_L$).

Com ambas as for as, podemos determinar o ngulo de ataque necess rio para o planador da seguinte forma:

$ \tan \phi =\displaystyle\frac{ S_p C_w }{ S_w C_L }$

(ID 15771)


(ID 15190)

ID:(466, 0)