Em coluna líquida
Storyboard 
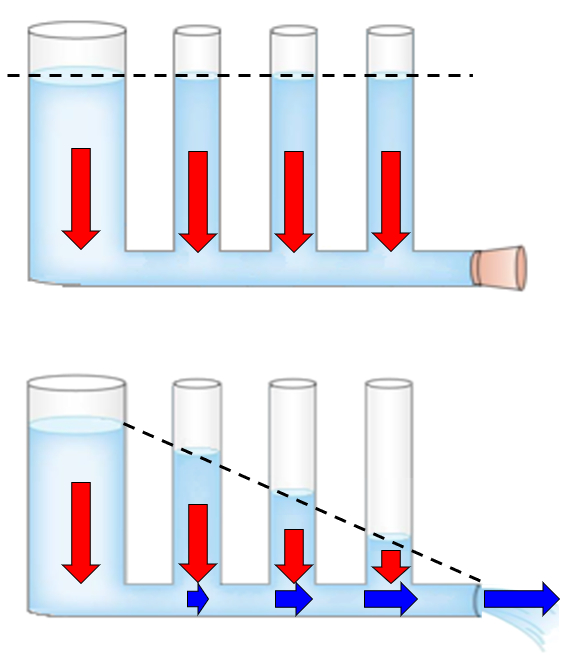
No caso de uma coluna de líquido, pode-se aplicar a lei de Bernoulli juntamente com o termo de pressão hidrostática. No entanto, é importante notar que, ao não considerar a viscosidade do líquido, a redução do nível ocorre de forma uniforme. Nesse sentido, pode ser modelado usando a equação de continuidade para determinar a velocidade de descida do cilindro.
Para uma coluna de líquido com saída na base, o comportamento é semelhante ao que é estimado com o princípio de Bernoulli. As diferenças surgem devido à formação de pequenos redemoinhos na saída, que efetivamente reduzem a área de saída e obstruem o fluxo. No entanto, o fluxo de um líquido de baixa viscosidade pode ser modelado na zona sem redemoinhos usando o princípio de Bernoulli.
ID:(1427, 0)
Em coluna líquida
Storyboard 
No caso de uma coluna de líquido, pode-se aplicar a lei de Bernoulli juntamente com o termo de pressão hidrostática. No entanto, é importante notar que, ao não considerar a viscosidade do líquido, a redução do nível ocorre de forma uniforme. Nesse sentido, pode ser modelado usando a equação de continuidade para determinar a velocidade de descida do cilindro. Para uma coluna de líquido com saída na base, o comportamento é semelhante ao que é estimado com o princípio de Bernoulli. As diferenças surgem devido à formação de pequenos redemoinhos na saída, que efetivamente reduzem a área de saída e obstruem o fluxo. No entanto, o fluxo de um líquido de baixa viscosidade pode ser modelado na zona sem redemoinhos usando o princípio de Bernoulli.
Variáveis
Cálculos
Cálculos
Equações
Se houver la diferença de pressão ($\Delta p$) entre dois pontos, conforme determinado pela equa o:
podemos usar la pressão da coluna de água ($p$), que definida como:
Isso resulta em:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Como la diferença de altura ($\Delta h$) :
la diferença de pressão ($\Delta p$) pode ser expressa como:
Usando a equa o de Bernoulli, podemos analisar o caso de uma coluna de gua que gera uma diferen a de press o:
e induz um fluxo de velocidade $v$ atrav s de um tubo, de acordo com:
Portanto, podemos estimar a velocidade como:
$v = \sqrt{2 g h}$
Essa velocidade, atrav s de uma se o de tubo com raio $R$, resulta em um fluxo:
$J = \pi R^2 v$
Se a coluna tem uma rea de se o transversal $S$ e sua altura diminui em rela o varia o da altura $h$ ao longo do tempo $t$, podemos aplicar a lei da continuidade, que estabelece:
Portanto, a equa o que descreve essa situa o :
Se na equa o
as constantes forem substitu das por
obtemos a equa o diferencial linear de primeira ordem
$\displaystyle\frac{dh}{dt}=\displaystyle\frac{1}{\tau_b} \sqrt{h_0 h}$
cuja solu o
Neste caso, pode-se assumir que la velocidade média do fluido no ponto 2 ($v_2$) representa uma velocidade nula e la velocidade média do fluido no ponto 1 ($v_1$) corresponde a la velocidade de fluxo ($v_s$). Portanto, para la diferença de velocidade entre superfícies ($\Delta v$) estabelece-se o seguinte:
$\Delta v = v_2 - v_1 = 0 - v_s = - v_s$
e para la velocidade média ($\bar{v}$) calcula-se:
$\bar{v} = \displaystyle\frac{v_1 + v_2}{2} = \frac{v_s}{2}$
Consequentemente, com ERROR:6673, que igual a la diferença de pressão ($\Delta p_s$), obtemos:
resultando em:
$\Delta p_s = \displaystyle\frac{1}{2} \rho v_s^2$
o que leva a:
O volume ($V$) para um tubo com la seção de tubo ($S$) constante e uma posição ($s$)
Se la seção de tubo ($S$) constante, a derivada temporal ser
$\displaystyle\frac{dV}{dt} = S\displaystyle\frac{ds}{dt}$
assim, com o fluxo de volume ($J_V$) definido por
e com la densidade de fluxo ($j_s$) associado a la posição ($s$) atrav s de
conclui-se que
Exemplos
Se houver uma altura da coluna ($h$) de l quido com la densidade líquida ($\rho_w$) sob o efeito da gravidade, utilizando la aceleração gravitacional ($g$), gerado ERROR:6673 conforme:
Este ERROR:6673 gera, atrav s do tubo de sa da com o comprimento do tubo ($\Delta L$), o raio do tubo ($R$) e la viscosidade ($\eta$), um fluxo de um fluxo de volume 1 ($J_{V1}$) de acordo com a lei de Hagen-Poiseuille:
Como esta equa o inclui la seção no ponto 2 ($S_2$), la densidade de fluxo 2 ($j_{s2}$) pode ser calculado atrav s de:
Com isso, obt m-se:
que corresponde a uma velocidade m dia.
Para modelar o sistema, os par metros-chave s o:
• Di metro interno do recipiente: 93 mm
• Di metro interno do canal de evacua o: 3,2 mm
• Comprimento do canal de evacua o: 18 mm
A altura inicial do l quido de 25 cm.
Vamos considerar o sistema de um balde cil ndrico com um orif cio de drenagem. Quando o tamp o removido, a gua come a a fluir de acordo com a press o existente. De acordo com o princ pio de Bernoulli, dentro do balde ($v\sim 0$), a velocidade zero, e temos:
$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \rho g h$
enquanto fora do balde ($h=0$), apenas a componente cin tica existe:
$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \displaystyle\frac{1}{2}\rho v^2$
Como ambas as express es s o iguais, temos:
$\displaystyle\frac{1}{2}\rho v^2=\rho g h$
o que nos d a velocidade como:
$v=\sqrt{2 g h}$
Para comparar com o experimento, podemos usar essa express o para estimar, com:
a dist ncia que o jato de gua deveria percorrer. Se plotarmos graficamente, observamos:
onde:
• os pontos vermelhos correspondem s medi es experimentais,
• os pontos azuis correspondem dist ncia calculada usando um fator de 0,11,
• os pontos transparentes correspondem dist ncia calculada usando um fator de 0,09.
Portanto, podemos concluir que o modelo de Bernoulli superestima a velocidade com que o balde se esvazia. Isso ocorre porque na regi o do orif cio de drenagem, os efeitos da viscosidade n o s o negligenci veis, e, portanto, a velocidade menor.
Se o programa Tracker for utilizado, poss vel medir a altura do menisco da coluna e o alcance do jato. A rela o entre os dois mostrada no seguinte gr fico:
Os dados registrados, que podem ser baixados como uma tabela do Excel no seguinte link tabela do Excel, s o os seguintes:
| Zeit [s] | H he [m] | Weite [m] |
| 0 | 2.23E-01 | 1.89E-01 |
| 4 | 2.14E-01 | 1.86E-01 |
| 8 | 2.04E-01 | 1.82E-01 |
| 12 | 1.94E-01 | 1.77E-01 |
| 16 | 1.86E-01 | 1.72E-01 |
| 20 | 1.79E-01 | 1.68E-01 |
| 24 | 1.71E-01 | 1.66E-01 |
| 28 | 1.63E-01 | 1.62E-01 |
| 32 | 1.54E-01 | 1.58E-01 |
| 36 | 1.46E-01 | 1.52E-01 |
| 40 | 1.39E-01 | 1.48E-01 |
| 44 | 1.32E-01 | 1.44E-01 |
| 48 | 1.24E-01 | 1.39E-01 |
| 52 | 1.18E-01 | 1.35E-01 |
| 56 | 1.11E-01 | 1.31E-01 |
| 60 | 1.06E-01 | 1.27E-01 |
| 64 | 9.88E-02 | 1.23E-01 |
| 68 | 9.29E-02 | 1.18E-01 |
| 72 | 8.70E-02 | 1.15E-01 |
| 76 | 8.11E-02 | 1.12E-01 |
| 80 | 7.52E-02 | 1.06E-01 |
| 84 | 7.12E-02 | 1.02E-01 |
| 88 | 6.51E-02 | 9.69E-02 |
| 92 | 6.00E-02 | 9.42E-02 |
| 96 | 5.58E-02 | 8.94E-02 |
| 100 | 5.09E-02 | 8.52E-02 |
| 104 | 4.70E-02 | 8.13E-02 |
| 108 | 4.34E-02 | 7.63E-02 |
| 112 | 3.97E-02 | 7.22E-02 |
| 116 | 3.49E-02 | 6.79E-02 |
| 120 | 3.15E-02 | 6.28E-02 |
| 124 | 2.91E-02 | 5.96E-02 |
| 128 | 2.58E-02 | 5.33E-02 |
| 132 | 2.23E-02 | 4.92E-02 |
| 136 | 1.98E-02 | 4.31E-02 |
| 140 | 1.71E-02 | 3.85E-02 |
| 144 | 1.54E-02 | 3.38E-02 |
| 148 | 1.28E-02 | 2.85E-02 |
| 152 | 1.11E-02 | 2.23E-02 |
| 156 | 9.17E-03 | 1.54E-02 |
| 160 | 7.15E-03 | 7.95E-03 |
Nota: E a nota o cient fica (zB. 1.2E+3 = 1.2x10^3 = 1200, y 1.2E-3 = 1.2x10^-3 = 0.0012)
Se tivermos um tubo com uma la seção de tubo ($S$) que se desloca uma dist ncia de o elemento de tubo ($\Delta s$) ao longo do seu eixo, tendo deslocado o elemento de volume ($\Delta V$), ent o igual a:
O fluxo de volume ($J_V$) corresponde a o volume de fluxo ($\Delta V$) que flui atrav s do canal em o tempo decorrido ($\Delta t$). Portanto, temos:
La densidade de fluxo ($j_s$) est relacionado com la distância percorrida em um tempo ($\Delta s$), que a dist ncia que o fluido percorre em o tempo decorrido ($\Delta t$), da seguinte maneira:
Uma densidade de fluxo ($j_s$) pode ser expresso em termos de o fluxo de volume ($J_V$) utilizando la seção ou superfície ($S$) atrav s da seguinte f rmula:
La superfície de um disco ($S$) de um raio do disco ($r$) calculada da seguinte forma:
Ao aplicar a equa o de Bernoulli em rela o a um ponto estacion rio no fluxo, verifica-se que la velocidade de fluxo ($v_s$) est associado a la diferença de pressão ($\Delta p_s$) quanto press o nesse ponto. Com la densidade ($\rho$), observa-se o seguinte:
A diferen a de altura, representada por la diferença de altura ($\Delta h$), implica que a press o em ambas as colunas diferente. Em particular, la diferença de pressão ($\Delta p$) uma fun o de la densidade líquida ($\rho_w$), la aceleração gravitacional ($g$) e la diferença de altura ($\Delta h$), da seguinte forma:
O princ pio da continuidade determina que o fluxo no primeiro ponto, que igual a la densidade de fluxo 1 ($j_{s1}$) vezes la seção no ponto 1 ($S_1$), deve ser igual ao fluxo no segundo ponto, dado por la densidade de fluxo 2 ($j_{s2}$) vezes la seção no ponto 2 ($S_2$). A partir disso, conclui-se que:
No caso de um l quido n o viscoso fluindo de forma laminar, a diferen a de press o gerada pela coluna a seguinte:
Isso resulta em um fluxo de velocidade $v$ atrav s de um tubo de acordo com o princ pio de Bernoulli:
Dada a velocidade e o raio do tubo, podemos calcular o fluxo, que est relacionado com o fluxo dentro da coluna atrav s da lei da continuidade. Por sua vez, isso se relaciona com a varia o da altura $h", como descrito em:
Se observarmos a equa o para o esvaziamento de uma coluna de l quido n o viscoso:
podemos condensar as constantes em uma unidade de tempo caracter stica:
Este valor representa o tempo necess rio para que a coluna seja completamente esvaziada e depende da altura inicial.
A equa o que descreve a evolu o da coluna de l quido viscoso que est drenando a seguinte:
Podemos reescrever esta equa o em termos do tempo caracter stico:
Ao realizar a integra o, obtemos:
Onde $h_0$ representa a altura inicial.
ID:(1427, 0)