User:
Structure of the Ear
Image
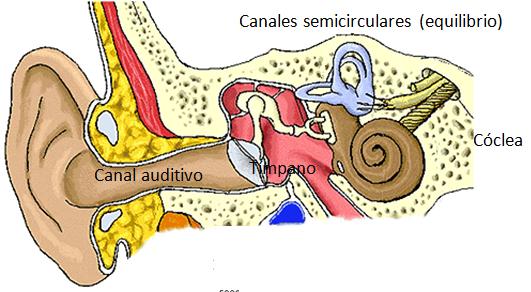
El oído está conformado por el canal auditivo, el tímpano, el yunque y la cóclea. El canal permite que el sonido alcance el tímpano que es una membrana capaz de oscilar y traspasar el movimiento amplificado por el yunque hasta la cloquea. Esta última funciona como un analizador de frecuencias que reporta al celebró la estructura del sonido recepcionado.
ID:(1674, 0)
Structure Coclea
Image
La cóclea tiene la forma de un caracol que se vuelve cada vez mas estrecho. Consta de dos cámaras separadas por una membrana que se extienden por todo el largo de la cóclea. El sonido penetra por el canal y la membrana entra en resonancia en una profundidad que depende del largo de onda. De esta forma se desglosa la señal en sus componentes según la frecuencia.
ID:(1866, 0)
Capacity of the Human Ear Hearing
Image
El oído humano puede captar sonidos con frecuencias entre 20 Hz y 20 kHz. Dicha capacidad se documenta con el numero de decibeles que se amortigua el sonido por frequencia:
De la gráfica se ve que la menor amortiguación es entre 200 Hz y 8 kHz.
ID:(1874, 0)
Noise level as function of the sound intensity
Equation
Just like in other human sensory systems, our hearing is capable of detecting pressure variations over a wide range $(10^{-5}-10^2 Pa)$. However, when we perceive a signal doubling, it doesn't correspond to double the pressure or sound intensity, but rather the square of these magnitudes. In other words, our signal detection capacity operates on a logarithmic and nonlinear scale.
Hence, the noise level, air ($L$) is indicated not in the sound Intensity ($I$) or the reference intensity, air ($I_{ref}$), but in the base ten logarithm of these magnitudes. Particularly, we take the lowest sound intensity we can perceive, the reference intensity, air ($I_{ref}$)
, and use it as a reference. The new scale is defined with as follows:
 $ L = 10 log_{10}\left(\displaystyle\frac{ I }{ I_{ref} }\right)$ |
ID:(3194, 0)
Noise level as function of the sound pressure, air
Equation
The noise level, air ($L$) encompasses a wide range of the sound pressure ($p$), making it useful to define a scale that mitigates this difficulty. To do so, we can work with the logarithm of the pressure normalized by a value corresponding to zero on this scale. If we take the minimum pressure that a person can detect, defined as the reference pressure ($p_{ref}$), we can define a scale using:
| $ L = 20 \log_{10}\left(\displaystyle\frac{ p }{ p_{ref} }\right)$ |
which starts at 0 for the audible range. In the case of air, the reference pressure ($p_{ref}$) is $20 \mu Pa$.
ID:(3407, 0)
Intensity reference values
Equation
The sound pressure level that we can detect with our ear, denoted as the reference pressure, water ($p_{ref}$), is $2 \times 10^{-5} , Pa$.
Since the sound Intensity ($I$) is associated with the sound pressure ($p$), the mean density ($\rho$), and the speed of sound ($c$), and is equal to
| $ I =\displaystyle\frac{ p ^2}{2 \rho c }$ |
we can calculate a value for the reference intensity, air ($I_{ref}$) based on the value of the reference pressure, water ($p_{ref}$):
| $ I_{ref} =\displaystyle\frac{ p_{ref} ^2}{2 \rho c }$ |
This is achieved with a density of $1.27 , kg/m^3$ and a sound speed of $331 , m/s$, equivalent to $9.5 \times 10^{-13} , W/m^2$.
ID:(3409, 0)
Noise Level Reduction with the Distance
Equation
$L=L_0 -40\log_{10}\left(\displaystyle\frac{r}{r_0}\right)$
ID:(3410, 0)