We have two eyes so that we are able to estimate distances and thus have a three-dimensional perception.

(ID 433)

Effect of seeing with two eyes

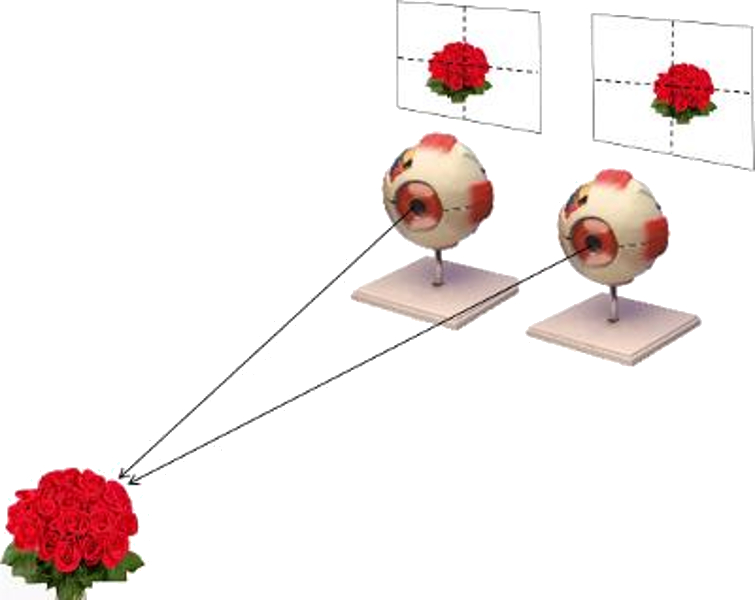
(ID 1818)

To model, we must diagram the situation that occurs with the images in both retinas. To do this, we studied the behavior of two beams in the plane formed between the object and the two retinas.

Suppose that the positions of the image in the left and right eye are s_i and s_r respectively. Regarding the eye, the distance between the lens and the retina can be defined as f and the distance between the eyes with d. Finally you can enter a distance r between the object a point between both crystals and \theta the angle that is being observed.

(ID 436)

The position of an object is perceived differently by each eye. The image is formed in different points with respect to the center of the retina:

From the difference in position we are able to determine the position of the object with respect to us.

(ID 1665)

By similarity of the triangles the proportion of the triangles of the left eye can be equalized. In the case of the major triangle the sides have lengths F+d/2-s_l and f+D while in the minor triangle they are F+d/2 and D. Therefore, we have:

\displaystyle\frac{F+d/2-s_l}{f+D}=\displaystyle\frac{F+d/2}{D}

(ID 434)

By similarity of the triangles the proportion of the triangles of the right eye can be equated. In the case of the major triangle, the sides have lengths F+d/2-s_r and f+D while in the minor triangle they are F+d/2 and D. Therefore, we have:

\displaystyle\frac{F-d/2-s_r}{f+D}=\displaystyle\frac{F-d/2}{D}

(ID 435)

From the equations of the triangle of the left and right eye we can determine the distance of the object in the plane of the eyes F. Clearing the distance D in the equation of similarity of triangles in the right eye and introducing it in the one of the left eye, we obtain:

Note: it can be shown that the sum s_r-s_l is always positive.

(ID 3424)

The distance of the object can be determined from the equations of the left and right eye triangle. In this way we obtain that the distance D is equal to the distance between the eyes d multiplied by the distance between retina and crystalline f divided by the sum of the displacements of the image s_r-s_l:

Note: it can be shown that the sum s_r-s_l is always positive.

(ID 3190)

To return to what is the real distance r and the angle \theta in which we observe the object, it is enough to use the inverse polar coordinate transformation:

(ID 3427)

To return to what is the real distance r and the angle \theta in which we observe the object, it is enough to use the inverse polar coordinate transformation:

(ID 3425)

The error of the estimate can be calculated by using the uncertainty propagation equations on the expression for the calculation of the distance. To simplify the calculation we can use the expression for the case that the object is in front of us.

(ID 193)

To simplify the solution of the model it is advisable to avoid working with the angle \theta. For this you can work simply with the lengths of the triangle edges D and F formed by the distance r and angle \theta of the position of the object.

The projected distance of the object is

Said change corresponds to moving from polar coordinates (r, \theta) to Cartesian in which the distance D corresponds to the variable x and F to the coordinate y.

(ID 3423)

To return to what is the real distance r and the angle \theta in which we observe the object, it is enough to use the inverse polar coordinate transformation:

(ID 3426)

$\Delta r=\displaystyle\frac{2r^2}{df}$

(ID 3283)

$r= \sqrt{D^2+F^2}$

(ID 3268)

$F=r\sin\theta$

(ID 3267)

$r=\displaystyle\frac{df}{2s}$

(ID 3271)

(ID 453)

(ID 454)

(ID 1824)

$\displaystyle\frac{\Delta r^2}{r^2}=\displaystyle\frac{\Delta s^2}{s^2}+\displaystyle\frac{\Delta d^2}{d^2}+\displaystyle\frac{\Delta f^2}{f^2}$

(ID 3282)