Processus de mélange en eaux peu profondes
Storyboard 
Les mécanismes de mélange dans les zones peu profondes sont générés par différents types d'ondes. Parmi eux se trouvent les ondes internes, les ondes de surface, l'interaction entre les ondes et les courants, les marées et le déferlement des vagues sur la côte.
ID:(1629, 0)
Processus de mélange en eaux peu profondes
Storyboard 
Les mécanismes de mélange dans les zones peu profondes sont générés par différents types d'ondes. Parmi eux se trouvent les ondes internes, les ondes de surface, l'interaction entre les ondes et les courants, les marées et le déferlement des vagues sur la côte.
Variables
Calculs
Calculs
Équations
De la m me mani re que a contrainte cinématique ($\tau_x$) est li a viscosité turbulente ($A$) et a longueur de mélange ($l$), il s'ensuit que :
Si a constante de Karman ($\kappa$), a profondeur totale ($H$) et a rugosité ($k$) sont utilis s :
et avec a vitesse de friction ($U_d$) :
nous obtenons :
Tout comme a contrainte cinématique ($\tau_x$) se rapporte a viscosité turbulente ($A$), le profil de vitesse ($u_z$) et a profondeur ($z$), il est d fini par
et peut tre int gr de le inégalité ($d$) A profondeur ($z$) pour obtenir la vitesse en utilisant l'expression suivante :
$u_z=\displaystyle\int_d^z\displaystyle\frac{\tau_x}{A}dz'$
Avec la formulation de a viscosité turbulente ($A$) en termes de a profondeur relative ($\xi$) ainsi que a profondeur totale ($H$), a rugosité ($k$) et a vitesse de friction ($U_d$), et en consid rant que
la formule suivante pour la vitesse est d riv e :
$u_z=\displaystyle\frac{U_d\sqrt{1-k}}{\kappa}(\ln(z/d) + \Phi(\xi,k))$
o
$\Phi=2[\arctan(\lambda)-\arctan(\lambda_0)]-\ln\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)$
est d fini avec
$\lambda=\sqrt{1-\xi}$
et
$\lambda=\sqrt{1-k}$
tant donn que sur une grande partie de la profondeur
$\ln(z/d) \gg \Phi(\xi,k)$
le profil de vitesse peut tre simplifi
Les s diments ont tendance se d poser au fond avec une taux de sédimentation ($\omega_s$), tandis que la diffusion, qui dans ce cas correspond au m lange g n r par les tourbillons, induit un flux gal a viscosité turbulente ($A$) et au gradient de ERROR:9478 en a profondeur ($z$), de la mani re suivante :
$A\displaystyle\frac{\partial c_z}{\partial z}+\omega_s c_z= 0$
En int grant cette expression, on obtient :
$c_z = \displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/A dz'}$
avec a longueur de mélange ($l$) :
nous avons :
$c_z=\displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/l\sqrt{\tau_x} dz'}$
ce qui donne :
$c_z=\displaystyle\frac{E}{\omega_s}\left(\displaystyle\frac{z}{d}\right)^{R_s}\Phi_c(\xi,k)$
avec le facteur de Rouse ($R_s$) et le numéro de réveil ($R_0$) :
o :
$\Phi=\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)^{2R_s}e^{2R_s[\arctan(\lambda)-\arctan(\lambda_0)]}$
avec :
$\lambda=\sqrt{1-\xi}$
et :
$\lambda=\sqrt{1-k}$
Comme sur une grande partie de la profondeur :
$\Phi\sim 1$
nous obtenons la distribution de concentration :
Tout comme a viscosité turbulente ($A$) est li a longueur de mélange ($l$), le profil de vitesse ($u_z$) et a profondeur ($z$) sont d finis comme suit :
et puisque a contrainte cinématique ($\tau_x$) est
l' limination du gradient donne
Exemples
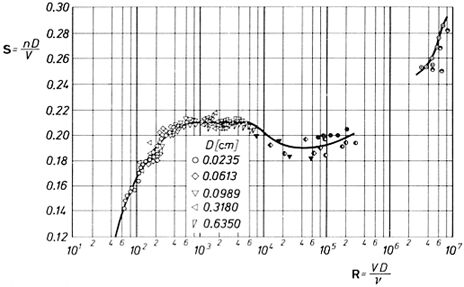
Le numéro de Strouhal ($St$) est reli empiriquement le le numéro de Reynold ($Re$). Le numéro de Strouhal ($St$) est associ a fréquence de génération de vortex ($\omega$), a vitesse de friction ($U_d$), et a profondeur totale ($H$) est
Cela permet d'estimer, via le le numéro de Reynold ($Re$), la fr quence laquelle la concentration peut changer les composants diffuser. Cependant, il faut garder l'esprit que le processus peut tre interrompu si la fr quence est inf rieure celle des mar es.
Si l'on suppose qu'il n'y a pas de vent la surface, on peut supposer qu'il n'y a pas de tension cet endroit. Par cons quent, il n'y aura de tension de l'eau que sur le fond. Cette tension diminuera lin airement du fond vers la surface. Pour simplifier la mod lisation, on peut utiliser la proportion entre a profondeur ($z$) et a profondeur totale ($H$), ce qui nous donne un facteur adimensionnel a profondeur relative ($\xi$). A contrainte cinématique ($\tau_x$) sera donc proportionnelle
$\tau_x \propto 1-\xi$
tant donn que a contrainte cinématique ($\tau_x$) est quivalent la densit d' nergie divis e par la densit , la valeur au fond doit tre proportionnelle au carr de la vitesse au fond. Cela est d crit dans le mod le avec a vitesse de friction ($U_d$) et signifie que
$\tau_x \propto U_d^2$
Enfin, il y a l'effet de a rugosité ($k$) du fond marin, c'est- -dire la proportion de le inégalité ($d$) et a profondeur totale ($H$). Cela signifie que a contrainte cinématique ($\tau_x$) doit tre corrig par un facteur analogue la profondeur :
$\tau_x \propto \displaystyle\frac{1-\xi}{1-k}$
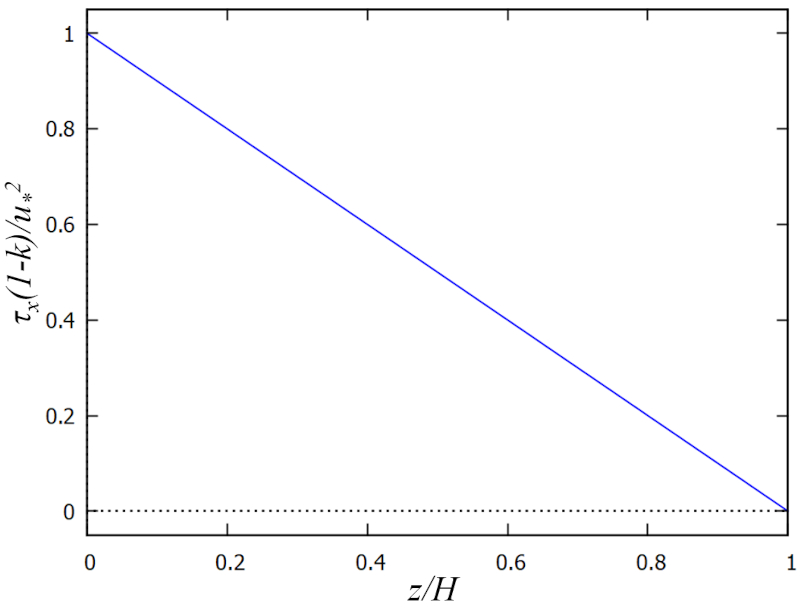
Ainsi, un mod le de la forme suivante est obtenu :
qui est repr sent graphiquement comme suit :
A longueur de mélange ($l$) correspond ce qui pourrait tre d crit comme la taille des tourbillons. proximit de la paroi, ces tourbillons ne peuvent avoir qu'une taille maximale gale la distance par rapport la paroi, qui est minimale. mesure que l'on se rapproche de la surface, ils peuvent devenir de plus en plus grands, donc la fonction doit atteindre un maximum ce point.
Pour simplifier la mod lisation, on peut utiliser le rapport entre a profondeur ($z$) et a profondeur totale ($H$), ce qui nous donne un facteur sans dimension a profondeur relative ($\xi$). Ainsi, une fonction simple qui r pond cette description est de la forme :
$l \propto \xi\left(1-\displaystyle\frac{1}{2}\xi\right)$
D'autre part, le mod le de couche limite de Prandtl montre que ces tourbillons repr sentent une fraction du flux avec une largeur gale a profondeur totale ($H$) et une proportion de a constante de Karman ($\kappa$), donc :
$l \propto \kappa H$
Enfin, il faut corriger l'effet de la rugosit de la m me mani re que pour la contrainte cin matique :
$l \propto \displaystyle\frac{\kappa H}{1-k}$
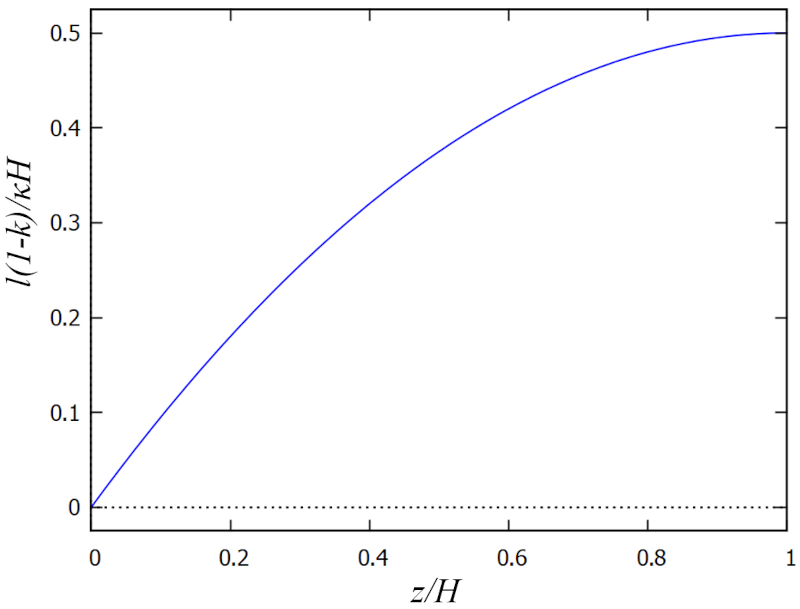
Par cons quent, a longueur de mélange ($l$) peut tre mod lis de la mani re suivante :
Lorsque Prandtl mod lise la formation de tourbillons pr s des parois, il tablit la relation entre a viscosité turbulente ($A$), a longueur de mélange ($l$) et le gradient de le profil de vitesse ($u_z$) en a profondeur ($z$) de la mani re suivante :
D'autre part, la force visqueuse typique, qui est mod lis e comme la viscosit multipli e par la surface de contact et le gradient de vitesse, correspond dans le cas des turbulences a contrainte cinématique ($\tau_x$) :
Des deux quations d coule la relation suivante :
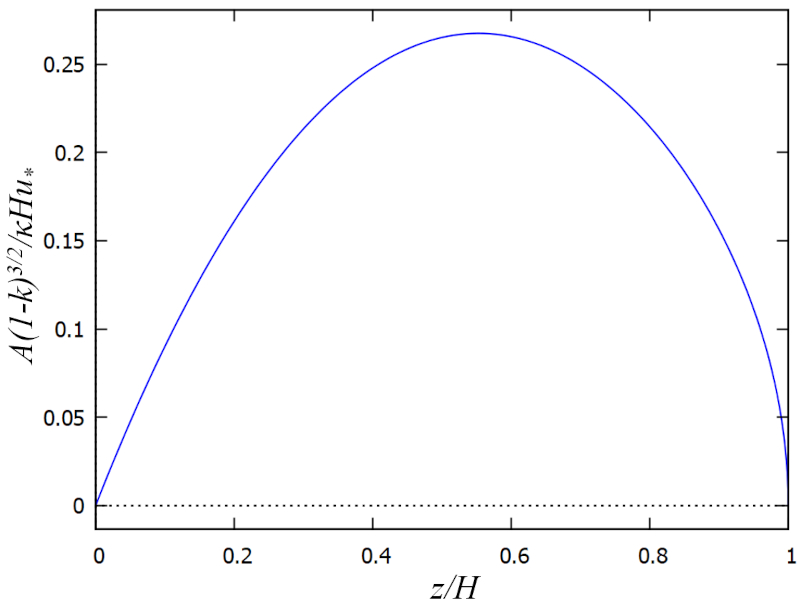
Cette relation permet de calculer a viscosité turbulente ($A$) en fonction de a contrainte cinématique ($\tau_x$) et de a longueur de mélange ($l$), qui sont mod lis s dans ce cas. Ainsi, avec a profondeur totale ($H$), a vitesse de friction ($U_d$), a rugosité ($k$), a profondeur relative ($\xi$) et a constante de Karman ($\kappa$) :
qui est repr sent ci-dessous :
Le r sultat est que la viscosit turbulente est maximale mi-profondeur et se r duit des valeurs minimales pr s du fond et pr s de la surface. En d'autres termes, dans ces zones, le m lange et la perte de quantit de mouvement sont moindres.
Puisque a contrainte cinématique ($\tau_x$) est gal a viscosité turbulente ($A$) et au gradient de le profil de vitesse ($u_z$) par rapport a profondeur ($z$), on peut int grer l quation pour obtenir le profil de vitesse :
$u_z = \displaystyle\int_d^z \frac{\tau_x}{A} dz'$
En effectuant cette int gration, et en utilisant a vitesse de friction ($U_d$), a constante de Karman ($\kappa$), a rugosité ($k$) et a profondeur relative ($\xi$), on obtient :
Cette expression correspond la c l bre loi logarithmique du profil de vitesses, d velopp e par Prandtl et Schlichting.
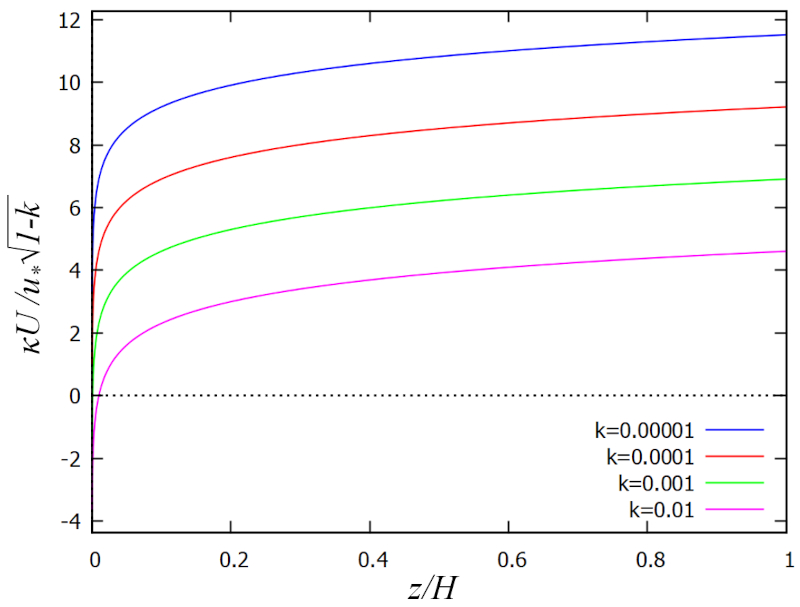
Le profil obtenu est repr sent dans le graphique suivant :
Ce profil permet galement d tablir une relation entre ERROR:9467 et a vitesse de friction ($U_d$) en fonction de a coefficient de traînée ($C_D$) :
De plus, a coefficient de traînée ($C_D$) peut tre estim partir de a rugosité ($k$) et a constante de Karman ($\kappa$) laide de :
Si l'on consid re le comportement du mat riau en suspension, deux facteurs principaux mergent. Tout d'abord, il y a une tendance la s dimentation avec une vitesse a taux de sédimentation ($\omega_s$), g n rant un flux d pendant de ERROR:9478, exprim comme suit :
$\omega_s c_z$
D'autre part, les tourbillons ont tendance m langer l'eau, produisant une diffusion qui transporte les s diments vers la surface. Ce flux, repr sent par a viscosité turbulente ($A$), est donn par le gradient de ERROR:9478 en a profondeur ($z$), gal :
$A\displaystyle\frac{\partial c_z}{\partial z}$
La distribution se forme lorsque les s diments atteignent l' quilibre, o le flux de s dimentation est gal la diffusion g n r e par les tourbillons vers la surface. En int grant les deux termes de l' quation avec le taux d'érosion ($E$) et le inégalité ($d$), nous obtenons la distribution :
$c_z=\displaystyle\frac{E}{\omega_s}e^{\displaystyle\int_d^z \omega_s/A dz'}$
Apr s avoir utilis l'expression obtenue pour a viscosité turbulente ($A$) avec le facteur de Rouse ($R_s$), a rugosité ($k$) et a profondeur relative ($\xi$), nous obtenons l'expression :
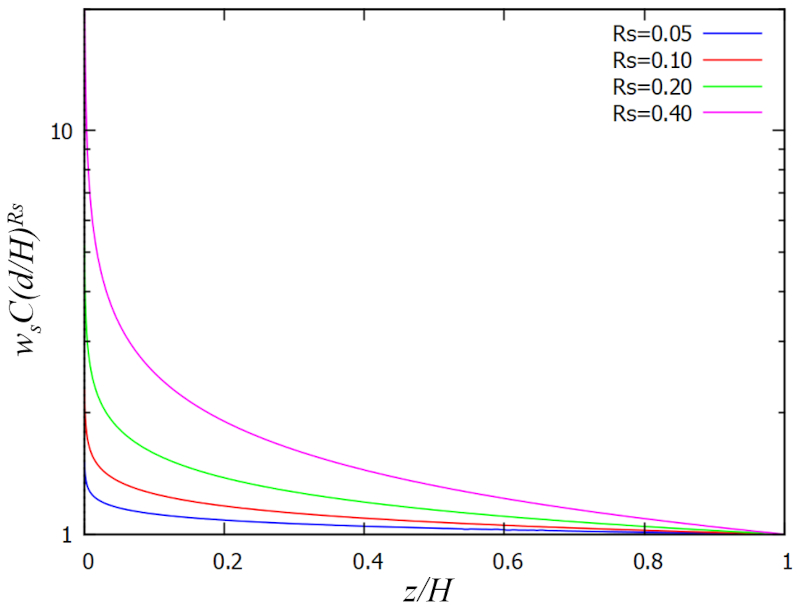
qui peut tre repr sent e graphiquement comme suit :
Le numéro de Strouhal ($St$) caract rise a fréquence de génération de vortex ($\omega$). Comparez la vitesse associ e a fréquence de génération de vortex ($\omega$) et sa taille avec celle de l' coulement repr sent par a profondeur totale ($H$).
Par cons quent, avec cela, nous avons
Le comportement du courant et des turbulences g n rer ou att nuer d pend de a rugosité ($k$) du fond marin. Cela est d fini en comparant le profil moyen de le inégalité ($d$) avec le profil de a profondeur totale ($H$) o il se trouve.
Par cons quent, on d finit que a rugosité ($k$) est
A profondeur relative ($\xi$) est d fini en fonction de a profondeur ($z$) et a profondeur totale ($H$), exprim comme suit :
Pour un coulement laminaire, a force visqueuse ($F_v$) peut tre calcul partir de les surfaces parallèles ($S$), a viscosité ($\eta$), a différence de vitesse entre les surfaces ($\Delta v$) et a distance entre les surfaces ($\Delta z$) en utilisant l' quation suivante :
Dans le cas d'un coulement turbulent, une analogie peut tre tablie en d finissant une viscosité turbulente ($A$) comme la viscosit divis e par la densit , associ e la force par surface et la densit , que nous appellerons a contrainte cinématique ($\tau_x$), calcul en fonction de le profil de vitesse ($u_z$) et a profondeur ($z$) de la mani re suivante :
En 1925, Prandtl a introduit le concept d'une couche limite o les tourbillons m langent le fluide et transf rent le moment de mani re similaire la mod lisation du transfert au niveau mol culaire, cr ant un comportement visqueux. La taille de cette zone est d finie comme a longueur de mélange ($l$) et l'effet est d crit par un analogue la viscosit correspondant a viscosité turbulente ($A$). Ceci peut tre estim avec le gradient de le profil de vitesse ($u_z$) dans a profondeur ($z$) en utilisant :
[1] Prandtl, Ludwig (1925). "Bericht ber Untersuchungen zur ausgebildeten Turbulenz" (Rapport sur les recherches en turbulence d velopp e). Z. Angew. Math. Mech. 5 (2): 136.
A contrainte cinématique ($\tau_x$) peut tre calcul partir de a viscosité turbulente ($A$) et a longueur de mélange ($l$) en utilisant la m thode suivante :
A contrainte cinématique ($\tau_x$) sera maximal pr s du fond oc anique et nul la surface, condition qu'il n'y ait pas de vent la surface de l'oc an. tant associ a vitesse de friction ($U_d$) au fond, mais devant tre corrig en raison de l'effet de a rugosité ($k$), il peut tre mod lis en fonction de a profondeur relative ($\xi$) comme suit :
La zone de m lange introduite par Prandtl, de taille a longueur de mélange ($l$), est estim e comme une fraction de l'ordre de a constante de Karman ($\kappa$) de a profondeur totale ($H$). De plus, il faut ajuster pour l'effet de a rugosité ($k$), et prendre en compte que a longueur de mélange ($l$) d pend de a profondeur relative ($\xi$), tant nul au fond et approximativement constant et maximal pr s de la surface. Par cons quent, elle peut tre mod lis e comme suit :
[1] Prandtl, Ludwig (1925). "Bericht ber Untersuchungen zur ausgebildeten Turbulenz" (Rapport sur les recherches en turbulence d velopp e). Z. Angew. Math. Mech. 5 (2): 136.
partir de mesures, on peut mod liser a viscosité turbulente ($A$) en fonction de a profondeur relative ($\xi$), a profondeur totale ($H$), a rugosité ($k$), a vitesse de friction ($U_d$) et a constante de Karman ($\kappa$) avec l'expression :
Le profil de vitesse ($u_z$) est une fonction de a profondeur relative ($\xi$) et des param tres a rugosité ($k$), a vitesse de friction ($U_d$) et a constante de Karman ($\kappa$), repr sent e de la mani re suivante :
ERROR:9467 est proportionnel a vitesse de friction ($U_d$), avec une constante de proportionnalit qui d pend de a constante de Karman ($\kappa$) et a rugosité ($k$), comme suit :
A vitesse de friction ($U_d$) est proportionnel ERROR:9467, avec une constante de proportionnalit a coefficient de traînée ($C_D$), qui repr sente la relation entre leurs nergies cin tiques respectives :
ERROR:9478 est une fonction de a profondeur relative ($\xi$) qui d pend de le taux d'érosion ($E$), a taux de sédimentation ($\omega_s$), a rugosité ($k$) et le facteur de Rouse ($R_s$), et se calcule de la mani re suivante :
La valeur le numéro de réveil ($R_0$) compare la vitesse de s dimentation, qui est en concurrence avec la diffusion associ e au courant au fond. Lorsqu'elle est combin e avec a taux de sédimentation ($\omega_s$), a vitesse de friction ($U_d$) et a constante de Karman ($\kappa$), elle donne :
La valeur le numéro de réveil ($R_0$) value la vitesse de s dimentation, qui est en concurrence avec la diffusion li e au courant au fond. Combin e avec a taux de sédimentation ($\omega_s$), a vitesse de friction ($U_d$) et a constante de Karman ($\kappa$), elle donne :
Dans les cas o le fond marin n'est pas lisse, a rugosité ($k$) existe et entra ne une correction du nombre de Rouse, que nous appelons le facteur de Rouse :
ID:(1629, 0)