Flujos de energía
Definición 
Si se observan los distintos procesos en torno al glaciar se pueden distinguir las siguientes fuentes de calor que pueden contribuir a derretir el hielo:
- radiación solar (VIS) y del ambiente (NIR)
- calor por derretimiento y congelación (fuente/sumidero)
- roce en la base
- calentamiento por deformación
- calor geométrico
que se resumen en la siguiente imagen:
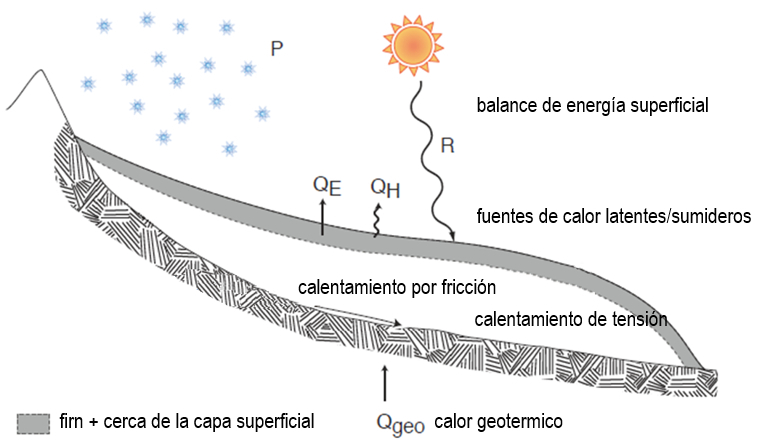
A esto se debe agregar el transporte de calor por efecto del agua de derretimiento que se desplaza dentro del glaciar.
ID:(9962, 0)
Calor geotermal
Imagen 
Al igual que se tiene radiación por el lado de la superficie existe geo-energía que llega hasta un nivel entre 40 y 120 mW/m^2 y que pueden contribuir a calentar la base del glaciar.
ID:(9971, 0)
Diagrama de fase del agua
Nota 
Para comprender el comportamiento del hielo es necesario conocer el diagrama de fase del agua:
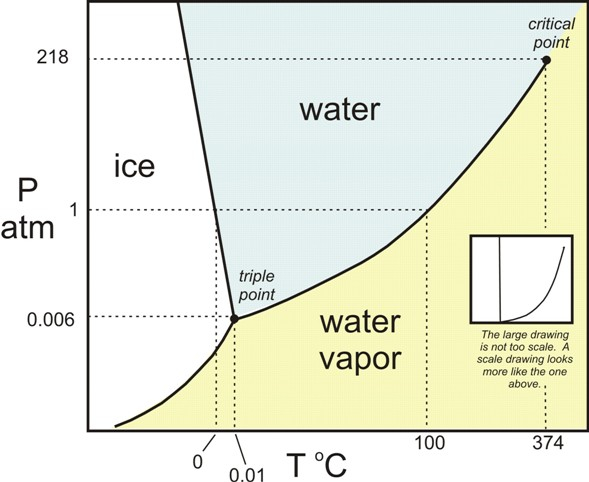
En el llama la atención la pendiente negativa del limite entre hielo y agua. Esto significa que con aumento de la presión el punto de congelación se reduce. Esto lleva a que si el hielo es expuesto a presión suficientemente alta puede ocurrir que su punto de congelación sea menor que la temperatura reinante y por ello se comience a derretir.
ID:(9992, 0)
Conducción de calor
Cita 
El derretimiento del glaciar ocurre cada vez que el calor generado en la superficie, interior o base sea superior a aquel que se desplaza por el gradiente existen.
Si el calor es inferior al gradiente el calor se transportara calentando el glaciar y sin originar derretimiento.
Si el calor generado es superior en la superficie, interior y/o base, se dará derretimiento en dichas zonas generando agua que en el caso de generación en superficie o interior percolará a la base o sera absorbido entre los granos de hielo.
El flujo generado por la conducción depende de la conductividad
Si se asume un gradiente de unos
ID:(9995, 0)
Perfil de temperatura
Ejercicio 
El perfil de temperatura va variando durante el año en función de la temperatura en la superficie y en la base del glaciar. En particular glaciares temperados tienden a tener un perfil tal que las temperaturas mayores están en la base y en la superficie:
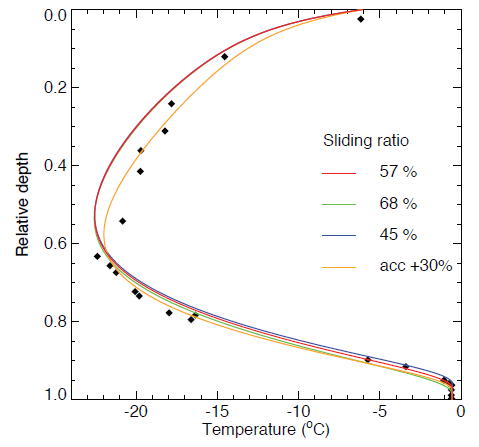
El perfil corresponde simulaciones realizadas por Funk et all (1994).
ID:(9994, 0)
Termodinámica de los Glaciares
Storyboard 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Si se observan los distintos procesos en torno al glaciar se pueden distinguir las siguientes fuentes de calor que pueden contribuir a derretir el hielo:
- radiaci n solar (VIS) y del ambiente (NIR)
- calor por derretimiento y congelaci n (fuente/sumidero)
- roce en la base
- calentamiento por deformaci n
- calor geom trico
que se resumen en la siguiente imagen:
A esto se debe agregar el transporte de calor por efecto del agua de derretimiento que se desplaza dentro del glaciar.
El calor especifico del hielo aumenta con la temperatura seg n la ecuaci n emp rica:
en donde el valor constante es
El calor latente especifico emp rico se puede modelar con la ecuaci n:
en donde el valor constante es
Si se desplaza un frente de congelaci n a una velocidad
donde
La deformaci n del hielo se puede describir como un flujo de una masa viscosa que disipa energ a seg n la traza de la velocidad de deformaci n
En un glaciar las componentes relevantes son la deformaci n cortante en que la superficie se desplaza en direcci n x mientras que la base en el origen del eje z tiende a no desplazarse o hacerlo en forma muy lenta. En otras palabras la deformaci n relevante es
se tiene que
mientras que la tensi n lo es en
con lo que la potencia por deformaci n en un volumen
se puede modelar para un elemento de secci n
como una intensidad
Si la base del glaciar se desplaza a una velocidad
donde
La tensi n en la base se puede asociar a la presi n necesaria para fusi n del hielo a la temperatura que exista en la base. Esto explica tambi n como el glaciar es capaz de avanzar sobre obst culos sin destruirlos, simplemente derriti ndose y volviendo a solidificarse detr s del obst culo.
Al igual que se tiene radiaci n por el lado de la superficie existe geo-energ a que llega hasta un nivel entre 40 y 120 mW/m^2 y que pueden contribuir a calentar la base del glaciar.
En la superficie se tiene la radiaci n (VIS) incidente que lleva a la absorci n
a ello se suma la radiaci n t rmica (NIR) que se recibe desde la atm sfera
De la energ a que se emite desde la superficie se tiene la radiaci n t rmica (NIR)
y los flujos relacionados a convecci n y calor latente (condensaci n de vapor de agua)
En promedio las contribuciones de la primera dos es igual a la perdida por efecto de las dos ultimas:
Para comprender el comportamiento del hielo es necesario conocer el diagrama de fase del agua:
En el llama la atenci n la pendiente negativa del limite entre hielo y agua. Esto significa que con aumento de la presi n el punto de congelaci n se reduce. Esto lleva a que si el hielo es expuesto a presi n suficientemente alta puede ocurrir que su punto de congelaci n sea menor que la temperatura reinante y por ello se comience a derretir.
Si se representa la frontera entre hielo y agua en el diagrama de fase como una recta, esta tendr la forma:
en donde
La constante
El derretimiento del glaciar ocurre cada vez que el calor generado en la superficie, interior o base sea superior a aquel que se desplaza por el gradiente existen.
Si el calor es inferior al gradiente el calor se transportara calentando el glaciar y sin originar derretimiento.
Si el calor generado es superior en la superficie, interior y/o base, se dar derretimiento en dichas zonas generando agua que en el caso de generaci n en superficie o interior percolar a la base o sera absorbido entre los granos de hielo.
El flujo generado por la conducci n depende de la conductividad
Si se asume un gradiente de unos
El perfil de temperatura va variando durante el a o en funci n de la temperatura en la superficie y en la base del glaciar. En particular glaciares temperados tienden a tener un perfil tal que las temperaturas mayores est n en la base y en la superficie:
ID:(1305, 0)
