Usuario:


Mecánica de los Glaciares
Storyboard

>Modelo

ID:(1306, 0)


Perfil de velocidad
Definición

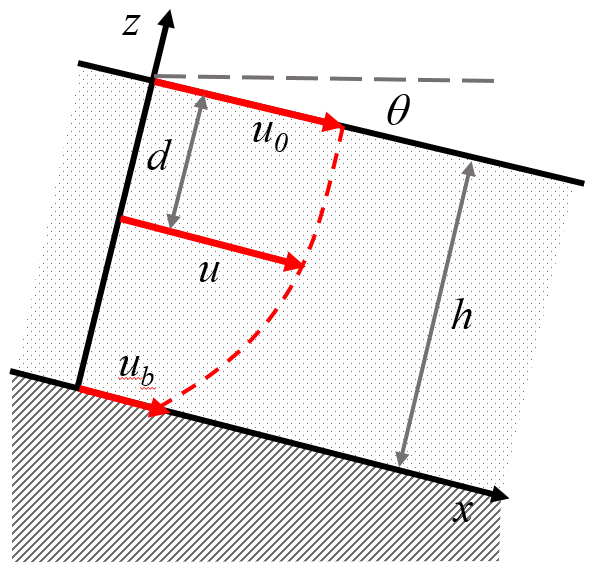
Como el glaciar se desplaza en forma lenta se le puede modelar como un flujo laminar con una velocidad u_0 en la superficie y una u_b en la base a una profundidad h. La velocidad en una profundidad d sera igual a u:

Perfil de la velocidad en la sección del glaciar

ID:(9973, 0)


Tensión de corte
Imagen

El glaciar se encuentra en un plano inclinado bajo un angulo \theta y esta expuesto a la fuerza de la gravedad y a las fuerzas de roce generadas por el fondo.

Cada elemento de volumen dV esta expuesto a la fuerza gravitacional

mg = \rho dV g

que tiene una componente perpendicular al plano sobre el que se encuentra el glaciar

\rho dV g\cos\theta

y una componente paralela a esta

F_g\sim \rho dV g\sin\theta\sim \rho S dz g\sin\theta

que en conjunto con la fuerza el roce con lo que se contorciona el hielo. La tensión asociada

\sigma=\displaystyle\frac{F_g}{S}

y se integra a lo largo de la profundidad del glaciar z se obtiene lo que se denomina la tensión de corte

que se observa en el hielo.

ID:(9952, 0)


Arrastrarse (creep)
Nota

El glaciar se arrastra gracias a la deformación de los cristales de hielo y el desplazamiento de estos entre si. Dicho proceso ocurre cada vez que la tensión basal sobrepasa los 50 kPa alcanzando por lo general valores entre 100 y 150 kPa.

ID:(9957, 0)


Causa del desplazamiento lento
Cita

En general el roce de la película de agua en la base del glaciar es muy pequeño (coeficiente del orden de 0.05) por lo que en general se espera que un glaciar se deslice a alta velocidad (metros por segundo). Sin embargo las velocidades observadas son metros por año o en caso extremos metros por día. La razón es, según J. Weertman (1957), son rocas que obstaculizan el avance. La teoría se denomina 'Tombstone Model' (modelo de lapidas funerarias) y considera que:

- el glaciar presiona sobre rocas del fondo
- el hielo en la superficie se descongela absorbiendo calor del entorno
- el agua fluye alrededor del obstáculo hasta llegar a una parte en que ya no esta expuesto a la presión por lo que se vuelve a solidificar
- el calor de la solidificación se conduce por la roca hasta la zona de la presión para volver a descongelar mas hielo

Lo descrito esta representado en la siguiente imagen

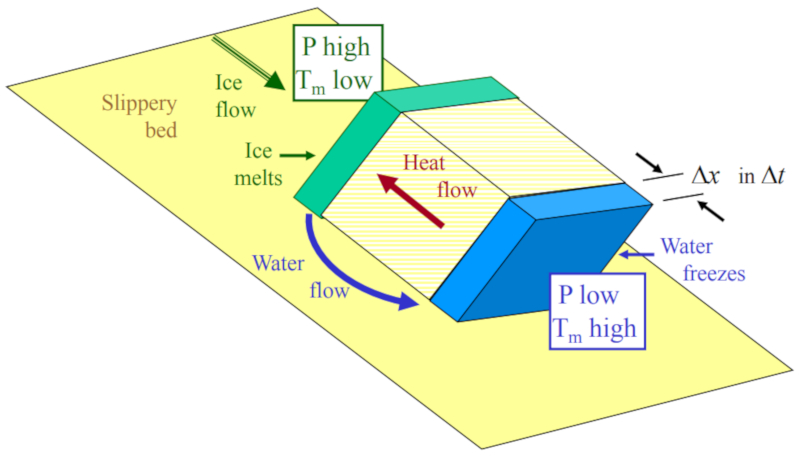
en que se asume un tamaño del obstáculo d\sim 1-5,m una conductividad de la roca \lambda_r\sim 0.5-5,W/mK.

ID:(10840, 0)


Mecánica de los Glaciares
Descripción

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$\theta$
theta
Angulo del plano de deslizamiento
rad
$l$
l
Calor latente específico del hielo
J/kg
$\lambda_r$
lambda
Conductividad del obstáculo
W/m K
$\gamma$
gamma
Constante del punto triple
K/Pa
$\epsilon_{xz}$
e=u_x/h
Deformación del glaciar
-
$\rho_i$
rho_i
Densidad del hielo del glaciar
kg/m^3
$u_x$
u_x
Desplazamiento de la superficie sobre la base
m
$z$
z
Distancia de base del glaciar
m
$n_g$
n_g
Exponente de la ley de Glen
-
$h$
h
Grosor del glaciar
m
$I_d$
I_d
Intensidad por calor de deformación
W/m^2
$d$
d
Tamaño del obstáculo
m
$\sigma_g$
sigma_g
Tensión de referencia de la ley de Glen
Pa
$\sigma$
sigma
Tensión en el hielo
Pa
$\tau_g$
tau_g
Tiempo de relajo de la ley de Glen
s
$b_b$
b_b
Velocidad de ablación en base
m/s
$\dot{u}$
u_t
Velocidad de desplazamiento
m/s
$v_b$
v_b
Velocidad de la base
m/s
$\dot{\epsilon}$
e_t
Velocidad de la deformación
Hz

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

Como el glaciar se desplaza en forma lenta se le puede modelar como un flujo laminar con una velocidad u_0 en la superficie y una u_b en la base a una profundidad h. La velocidad en una profundidad d sera igual a u:

Perfil de la velocidad en la secci n del glaciar

(ID 9973)

El glaciar se encuentra en un plano inclinado bajo un angulo \theta y esta expuesto a la fuerza de la gravedad y a las fuerzas de roce generadas por el fondo.

Cada elemento de volumen dV esta expuesto a la fuerza gravitacional

mg = \rho dV g

que tiene una componente perpendicular al plano sobre el que se encuentra el glaciar

\rho dV g\cos\theta

y una componente paralela a esta

F_g\sim \rho dV g\sin\theta\sim \rho S dz g\sin\theta

que en conjunto con la fuerza el roce con lo que se contorciona el hielo. La tensi n asociada

\sigma=\displaystyle\frac{F_g}{S}

y se integra a lo largo de la profundidad del glaciar z se obtiene lo que se denomina la tensi n de corte

que se observa en el hielo.

(ID 9952)

La ley de Glen establece como la velocidad de la deformaci n d\epsilon/dt depende de la tensi n \sigma a la que esta expuesto el material mediante



con n\sim 3 un exponente y A con valores entre 24\times 10^{-25} s^{-1}Pa^{-3} a cero grados y 3.5\times 10^{-25} s^{-1}Pa^{-3} a -10 grados. La constante A es poco intuitiva y la ley se puede reformular como

$\dot{\epsilon}=\displaystyle\frac{1}{\tau_g}\left(\displaystyle\frac{\sigma}{\sigma_g}\right)^{n_g}$

en donde la cl sica constante introducida por Glen se ha re-definido mediante una tensi n de referencia \sigma_g, un tiempo de relajaci n \tau_g y n un exponente con un valor promedio de 3.

En Deformation of Glacial Materials (Geological Society Special Publication No. 176) D.H.B. Irving et al propone un modelo seg n el cual se podr a aproximar la tensi n con de Glen con 25 kPa y el tiempo de relajaci n con 2030 a os.

(ID 9956)

El glaciar se arrastra gracias a la deformaci n de los cristales de hielo y el desplazamiento de estos entre si. Dicho proceso ocurre cada vez que la tensi n basal sobrepasa los 50 kPa alcanzando por lo general valores entre 100 y 150 kPa.

(ID 9957)

Al encontrarse el glaciar en una superficie similar a un plano inclinado en que el roce evita un deslizamiento, la masa de este genera un torque que lleva a una deformaci n en que se desplaza en la superficie u_x en direcci n del eje x en funci n de su distancia a la base dado por la altura \Delta z\sim h con lo que la deformaci n es

$\epsilon\sim\displaystyle\frac{u_x}{h}$

(ID 9970)

Con la ley de Glen

$\dot{\epsilon}=\displaystyle\frac{1}{\tau_g}\left(\displaystyle\frac{\sigma}{\sigma_g}\right)^{n_g}$



la deformaci n

$\epsilon\sim\displaystyle\frac{u_x}{h}$



y la tensi n de corte

$\sigma = \rho_i\,g\,z\,\sin\theta$



se obtiene la ecuaci n para el perfil de la velocidad

$\dot{u} = \displaystyle\frac{h}{\tau_g}\left(\displaystyle\frac{\rho_i\,g\,z\,\sin \theta }{ \sigma_g }\right)^{n_g}$

que ser refiere a la velocidad a una altura z desde la base y en funci n de la velocidad en la base v_b.

(ID 9974)

Con la intensidad generada por la deformaci n

$dI_d=\rho_i\,\dot{u}\,g\,\sin\theta\,dz$



y la velocidad del glaciar en una altura z desde el fundo

$\dot{u} = \displaystyle\frac{h}{\tau_g}\left(\displaystyle\frac{\rho_i\,g\,z\,\sin \theta }{ \sigma_g }\right)^{n_g}$



se tiene que se puede reemplazar e integrar sobre toda la altura resultando

$I_d = \displaystyle\frac{1}{(n_g+1)\tau_g}\displaystyle\frac{(\rho_i\,g\,h\,\sin\theta )^{n_g+1}}{\sigma_g^{n_g}}$

(ID 9999)

En general el roce de la pel cula de agua en la base del glaciar es muy peque o (coeficiente del orden de 0.05) por lo que en general se espera que un glaciar se deslice a alta velocidad (metros por segundo). Sin embargo las velocidades observadas son metros por a o o en caso extremos metros por d a. La raz n es, seg n J. Weertman (1957), son rocas que obstaculizan el avance. La teor a se denomina 'Tombstone Model' (modelo de lapidas funerarias) y considera que:

- el glaciar presiona sobre rocas del fondo
- el hielo en la superficie se descongela absorbiendo calor del entorno
- el agua fluye alrededor del obst culo hasta llegar a una parte en que ya no esta expuesto a la presi n por lo que se vuelve a solidificar
- el calor de la solidificaci n se conduce por la roca hasta la zona de la presi n para volver a descongelar mas hielo

Lo descrito esta representado en la siguiente imagen

en que se asume un tama o del obst culo d\sim 1-5,m una conductividad de la roca \lambda_r\sim 0.5-5,W/mK.

(ID 10840)

Para una tajada del ancho \Delta x y area de ancho y alto d el hielo de densidad \rho_i que requiere de una energ a igual a

\Delta Q = l\rho_id^2\Delta x

donde l es la entalpia o calor especifico de fusi n del hielo. Si se piensa en un obstaculo cubico el largo en que se conduce el calor es tambien d que con una conductividad de la roca \lambda_r se transmite en un tiempo \Delta t seg n:

\displaystyle\frac{\Delta Q}{\Delta t}=\displaystyle\frac{l d^2 \rho_i\Delta x}{\Delta t}=\displaystyle\frac{\lambda\Delta T}{d}

donde \Delta T es la diferencia de temperatura. Como esta es igual a

\Delta T=\gamma\Delta p

en donde la presi n es la componente vertical de la columna de hielo

\Delta p=\rho_i g h\sin\theta

donde h es la altura del glaciar y \theta el angulo de la inclinaci n del plano de deslizamiento.

De esta forma la velocidad

v_b=\displaystyle\frac{\Delta x}{\Delta t}

es

$ v_b =\displaystyle\frac{ \lambda_r \gamma g h \sin \theta }{ l d ^2}$

(ID 10839)

La base del glaciar se desplaza por el peso del glaciar y la situaci n que se da con obst culos en su camino

$ v_b =\displaystyle\frac{ \lambda_r \gamma g h \sin \theta }{ l d ^2}$



En base a la velocidad en funci n de la altura z desde la base del glaciar

$\dot{u} = \displaystyle\frac{h}{\tau_g}\left(\displaystyle\frac{\rho_i\,g\,z\,\sin \theta }{ \sigma_g }\right)^{n_g}$



se tiene que la velocidad en la superficie es

$v(z) = v_b+\displaystyle\frac{h}{\tau_g}\left(\displaystyle\frac{\rho_ig\,z\,\sin \theta}{\sigma_g}\right)^{n_g}$

(ID 9975)

ID:(1306, 0)