Usuario:
Bombas de rotor y centrifugas
Imagen 
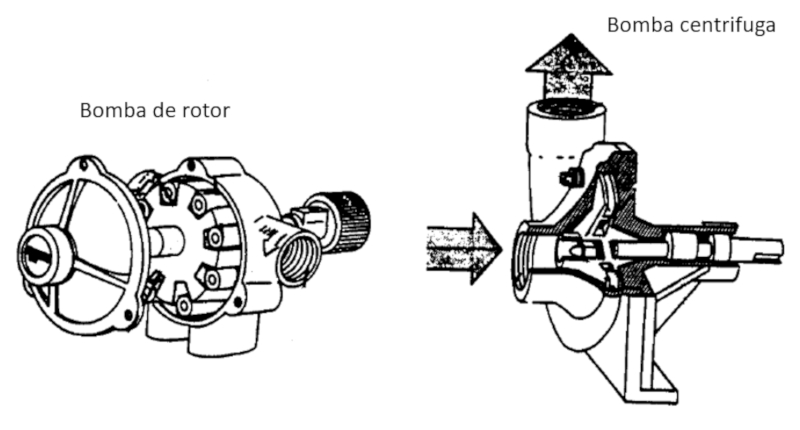
Los dos principales mecanismos sobre los que se basan las bombas son de rotor (desplazan liquido) y las centrifugas que aceleran el liquido radialmente para generar el movimiento.
ID:(12894, 0)
Comparación entre bombas
Nota
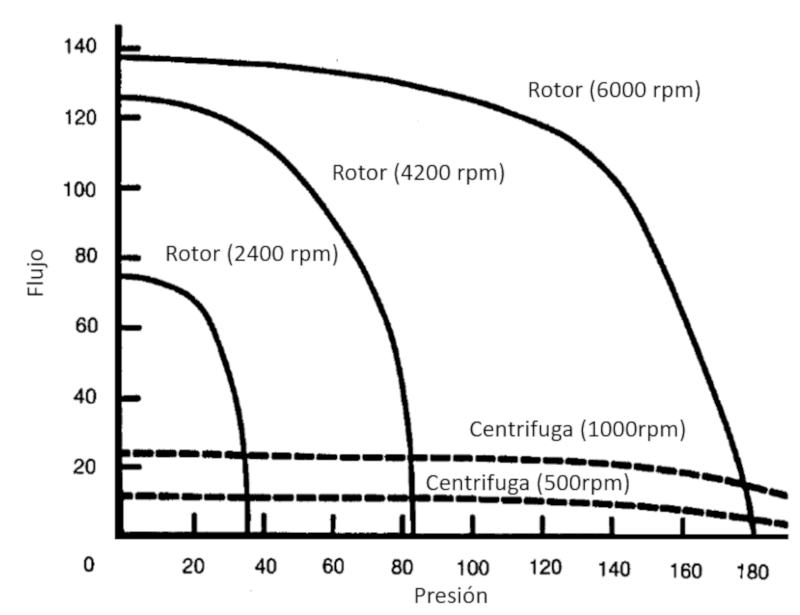
Las bombas centrifugas logran un menor flujo pero parejo sobre un mayor rango de diferencia de presiones:
ID:(12896, 0)
Conductividad hidráulica en paralelo
Ejercicio
Si se tienen tres resistencias hidráulicas $R_{h1}$, $R_{h2}$ y $R_{h3}$, la suma en serie de las resistencias será:
 $ K_{pt} = \displaystyle\sum_k K_{hk}$
|
ID:(3631, 0)
Bombas, Valvulas y Actuadores
Storyboard
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuaci n siguiente:
Adem s, utilizando la relaci n para la resistencia hidráulica ($R_h$):
se obtiene el resultado final:
Dado que la resistencia hidráulica ($R_h$) es igual a la conductancia hidráulica ($G_h$) seg n la siguiente ecuaci n:
y dado que la conductancia hidráulica ($G_h$) se expresa en t rminos de la viscosidad ($\eta$), el radio del tubo ($R$) y el largo de tubo ($\Delta L$) de la siguiente manera:
podemos concluir que:
Para el caso de que no exista presi n histrostatica la ley de Bernoulli para la densidad ($\rho$), la presión en la columna 1 ($p_1$), la presión en la columna 2 ($p_2$), la velocidad media del fluido en el punto 1 ($v_1$) y la velocidad media del fluido en el punto 2 ($v_2$)
se puede reescribir con el diferencial de la presión ($\Delta p$)
y teniendo presente de que
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
con
y
se tiene que
Ejemplos
Los dos principales mecanismos sobre los que se basan las bombas son de rotor (desplazan liquido) y las centrifugas que aceleran el liquido radialmente para generar el movimiento.
Las bombas centrifugas logran un menor flujo pero parejo sobre un mayor rango de diferencia de presiones:
El diferencial de la presión ($\Delta p$) se puede calcular de la velocidad promedio ($\bar{v}$) y la diferencia de velocidad entre superficies ($\Delta v$) con la densidad ($\rho$) mediante
que permite ver el efecto de la melocidad promedio de un cuerpo y de la diferencia de esta entre sus superficies como se observa en un ala de avion o ave.
Darcy reescribe la ecuaci n de Hagen Poiseuille de modo que la diferencia de presión ($\Delta p$) es igual a la resistencia hidráulica ($R_h$) por el flujo de volumen ($J_V$):
Dado que la resistencia hidráulica ($R_h$) es igual al inverso de la conductancia hidráulica ($G_h$), podemos calcularlo a partir de la expresi n de este ltimo. De esta manera, podemos identificar par metros relacionados con la geometr a (el largo de tubo ($\Delta L$) y el radio del tubo ($R$)) y el tipo de l quido (la viscosidad ($\eta$)), que pueden ser denominados colectivamente como una resistencia hidráulica ($R_h$):
Si se tienen tres resistencias hidr ulicas $R_{h1}$, $R_{h2}$ y $R_{h3}$, la suma en serie de las resistencias ser :
ID:(1680, 0)