Usuario:


Energía del gas
Storyboard

>Modelo

ID:(1612, 0)


Energía de una partícula con $f$ grados de libertad
Definición

Energía de una partícula con f grados de libertad

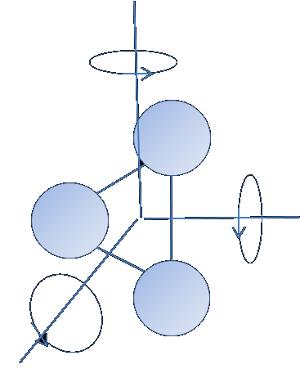
ID:(1960, 0)


Energía del gas
Descripción

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$e$
e
Energía promedio de una Partícula
J
$E$
E
Energía total
J
$f$
f
Grados de libertad
-
$m$
m
Masa de la partícula
kg
$n$
n
Número de moles
mol
$\langle v^2\rangle$
v^2
Promedio de Velocidad al cuadrado
m^2/s^2
$T$
T
Temperatura absoluta
K

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

Energ a de una part cula con f grados de libertad

(ID 1960)

Como las part culas pueden tener una velocidad distinta trabajaremos con valores promedio. En tal caso la energ a cin tica promedio es

$\langle\epsilon\rangle=\displaystyle\frac{1}{2}m\langle v^2\rangle$

es el promedio del cuadrado de la velocidad.

(ID 3932)

Con la constante de Boltzmann\\n\\n

$k_B=\displaystyle\frac{R}{N_A}$

\\n\\ny la energ a por part cula\\n\\n

$\langle\epsilon\rangle=\displaystyle\frac{3RT}{2N_A}$



se puede escribir esta como

$\langle\epsilon\rangle=\displaystyle\frac{3}{2}kT$

(ID 3224)

Si la part cula tiene f grados de libertad, la energ a puede ser calculada en funci n de la temperatura absoluta T y la constante de Boltzmann k_B mediante

$ \langle\epsilon\rangle =\displaystyle\frac{ f }{2} k_B T $

(ID 3940)

La energ a E contenida en n moles de part culas ser la energ a promedio multiplicada por el numero de moles n y el numero de Avogadro N_A

$E=nN_A\langle\epsilon\rangle$

(ID 3933)

ID:(1612, 0)