Utilisateur:
Action et réaction
Storyboard 
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Comme a variation de l'élan ($\Delta p$) est gal a masse d'inertie ($m_i$) par a différence de vitesse ($\Delta v$), nous avons :
Pour le cas o la masse est constante, la variation de la quantit de mouvement peut tre crite avec le moment ($p$) et le moment initial ($p_0$), ce qui, combin avec a vitesse ($v$) et a vitesse initiale ($v_0$), donne :
$\Delta p = p - p_0 = m_i v - m_i v_0 = m_i ( v - v_0 ) = m_i \Delta v$
o a différence de vitesse ($\Delta v$) est calcul avec :
ainsi, on obtient :
Comme a variation de l'élan ($\Delta p$) est gal a masse d'inertie ($m_i$) par a différence de vitesse ($\Delta v$), nous avons :
Pour le cas o la masse est constante, la variation de la quantit de mouvement peut tre crite avec le moment ($p$) et le moment initial ($p_0$), ce qui, combin avec a vitesse ($v$) et a vitesse initiale ($v_0$), donne :
$\Delta p = p - p_0 = m_i v - m_i v_0 = m_i ( v - v_0 ) = m_i \Delta v$
o a différence de vitesse ($\Delta v$) est calcul avec :
ainsi, on obtient :
Exemples
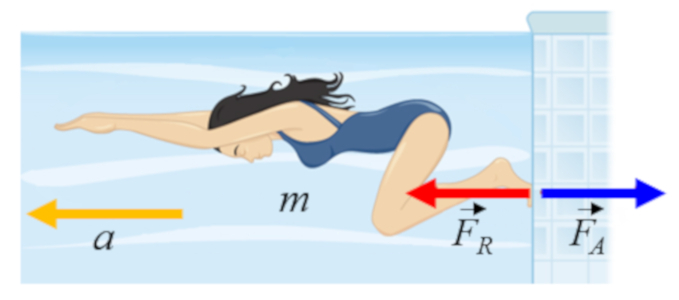
Quand une nageuse se propulse, elle exerce une force de une force d'action ($F_A$) sur le mur de la piscine, ce qui son tour g n re une force de une force de réaction ($F_R$) sur son corps, propulsant ainsi son d placement:
Si nous essayons d\'exercer une force contre un mur, nous constatons que la principale limitation est due l\'adh rence de nos chaussures au sol. Si le sol est lisse, nous commencerons g n ralement glisser, limitant ainsi la force que nous pouvons exercer.
Il est int ressant de noter que si nous poussons dans une direction non horizontale, la composante verticale affectera notre force verticale contre le sol. En d\'autres termes, la r action verticale notre action contre le mur entra nera une augmentation (si nous poussons plut t vers le haut) ou une diminution (si nous poussons plut t vers le bas) de notre poids.
chaque fois que nous marchons, nous devons propulser notre corps chaque pas. Pour ce faire, nous pla ons le pied sur le sol et, en supposant qu\'il ne glisse pas en raison de la friction, nos muscles exercent une force sur notre corps qui le propulse en avant et transmet la r action au pied, qui la transmet son tour au sol (la plan te) :
tant donn que la plan te est gigantesque, nous n\'observons pas directement l\'effet de cette r action. Cependant, si nous nous trouvons sur un objet plus petit comme un cylindre, nous pouvons induire son roulement en avan ant par rapport notre position sur le cylindre, tandis que le cylindre roule dans la direction oppos e.
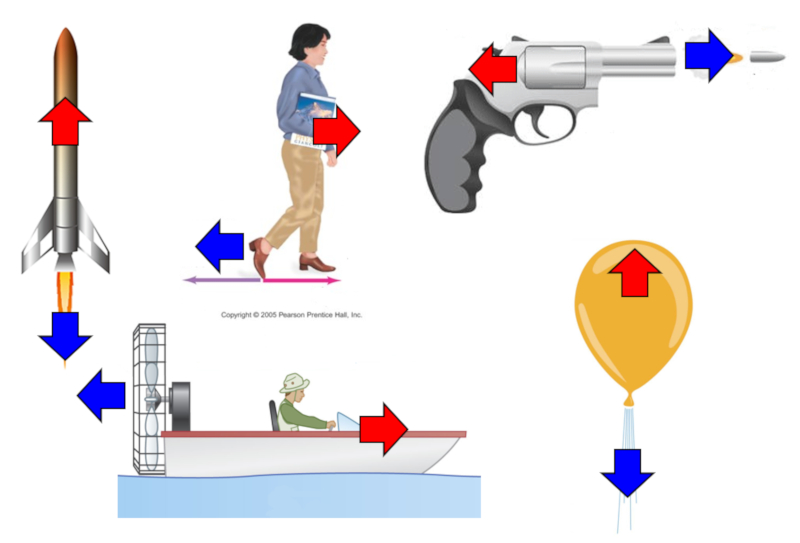
Un aspect important de la force est qu'elle ne peut pas tre cr e partir de rien. Chaque fois que nous tentons de g n rer une force d'action ($F_A$) (une action), une force de réaction ($F_R$) sera in vitablement g n r avec la m me magnitude mais une direction oppos e :
En d'autres termes, les forces se cr ent toujours par paires, et la somme de ces paires est toujours gale z ro.
A force ($F$) est d fini comme a variation de l'élan ($\Delta p$) par le temps écoulé ($\Delta t$), qui est d fini par la relation :
A force ($F$) est d fini comme a variation de l'élan ($\Delta p$) par le temps écoulé ($\Delta t$), qui est d fini par la relation :
Dans le cas o a masse d'inertie ($m_i$) est constant, a variation de l'élan ($\Delta p$) est proportionnel a différence de vitesse ($\Delta v$) :
Dans le cas o a masse d'inertie ($m_i$) est constant, a variation de l'élan ($\Delta p$) est proportionnel a différence de vitesse ($\Delta v$) :
ID:(755, 0)
