Utilizador:
Interceptar em velocidade constante
Storyboard 
Os objetos podem se interceptar quando coincidem na posição em um mesmo momento. Para isso acontecer, eles devem se deslocar a partir de seus respectivos pontos iniciais com velocidades que os levem a coincidir em posição e tempo no final da jornada.
ID:(445, 0)
Interceptar em velocidade constante
Descrição
Os objetos podem se interceptar quando coincidem na posição em um mesmo momento. Para isso acontecer, eles devem se deslocar a partir de seus respectivos pontos iniciais com velocidades que os levem a coincidir em posição e tempo no final da jornada.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Com la distância percorrida em um tempo ($\Delta s$) com la posição ($s$) e la velocidade ($s_0$):
| $ \Delta s = s - s_0 $ |
e o tempo decorrido ($\Delta t$) com o tempo ($t$) e o tempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
A equa o para a velocidade m dia:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
pode ser escrita como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
portanto, resolvendo para ela obtemos:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Com la distância percorrida em um tempo ($\Delta s$) com la posição ($s$) e la velocidade ($s_0$):
| $ \Delta s = s - s_0 $ |
e o tempo decorrido ($\Delta t$) com o tempo ($t$) e o tempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
A equa o para a velocidade m dia:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
pode ser escrita como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
portanto, resolvendo para ela obtemos:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Se partirmos de la velocidade ($s_0$) e quisermos calcular la distância percorrida em um tempo ($\Delta s$), é necessário definir um valor para la posição ($s$).
Em um sistema unidimensional, la distância percorrida em um tempo ($\Delta s$) é obtido simplesmente subtraindo la velocidade ($s_0$) de la posição ($s$), resultando em:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Se partirmos de la velocidade ($s_0$) e quisermos calcular la distância percorrida em um tempo ($\Delta s$), é necessário definir um valor para la posição ($s$).
Em um sistema unidimensional, la distância percorrida em um tempo ($\Delta s$) é obtido simplesmente subtraindo la velocidade ($s_0$) de la posição ($s$), resultando em:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Exemplos
Durante o processo de interse o, dois corpos se deslocam de forma que coincidam em la posição de interseção ($s$) e o tempo de interseção ($t$).
Para isso, cada corpo deve partir de suas respectivas posi es e tempos iniciais, com deslocamentos de la velocidade do primeiro estágio ($v_1$) e la velocidade do primeiro estágio ($v_1$), respectivamente, de modo que a coincid ncia ocorra.
(ID 15394)
No caso de intercep o, temos dois corpos que se deslocam de forma a coincidir em um tempo de interseção ($t$) na sua ERROR:10258,0.
Para este efeito, cada corpo:
• Inicia em o tempo inicial do primeiro objeto ($t_1$) com la posição inicial do primeiro objeto ($s_1$) como sua posi o inicial e la velocidade do primeiro estágio ($v_1$) como deslocamento.
• Inicia em o tempo inicial do segundo objeto ($t_2$) com la posição inicial do segundo objeto ($s_2$) como sua posi o inicial e la velocidade do segundo estágio ($v_2$) como deslocamento.
Estas condi es devem ser satisfeitas para que ocorra a intercep o.
Assim, os diagramas da posi o ao longo do tempo podem ser acoplados como na seguinte representa o:
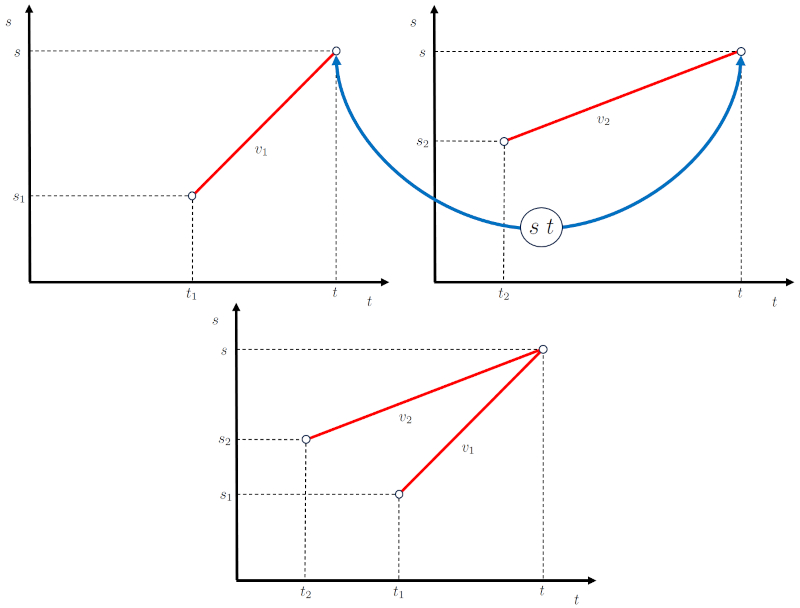
(ID 15505)
No caso de uma interse o ou colis o entre dois objetos, comum que la velocidade do primeiro estágio ($v_1$) e la velocidade do segundo estágio ($v_2$) precisem ser tais que ocorra a coincid ncia.
Isso significa que la distância percorrida pelo primeiro objeto ($\Delta s_1$) e la tempo de percurso do primeiro objeto ($\Delta t_1$) devem resultar em uma velocidade do primeiro estágio ($v_1$),
| $ v_1 \equiv\displaystyle\frac{ \Delta s_1 }{ \Delta t_1 }$ |
de modo que com la distância percorrida pelo segundo objeto ($\Delta s_2$) e la tempo de percurso do segundo objeto ($\Delta t_2$), obtemos uma velocidade do segundo estágio ($v_2$),
| $ v_2 \equiv\displaystyle\frac{ \Delta s_2 }{ \Delta t_2 }$ |
para que eles coincidam eventualmente em tempo e espa o (posi o):
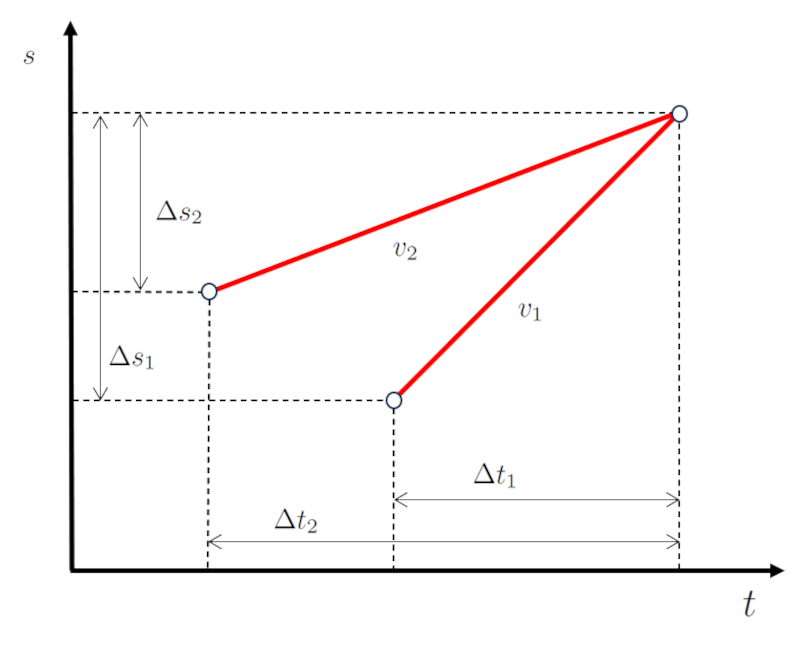
(ID 12509)
No caso de um movimento em que dois objetos se interceptam, como la posição de interseção ($s$) e o tempo de interseção ($t$), comum para ambos. Portanto, se para o primeiro objeto o tempo inicial do primeiro objeto ($t_1$) e la posição inicial do primeiro objeto ($s_1$) com la velocidade do primeiro estágio ($v_1$) forem atendidos:
| $ s = s_1 + v_1 ( t - t_1 )$ |
e para o segundo objeto o tempo inicial do segundo objeto ($t_2$) e la posição inicial do segundo objeto ($s_2$) com la velocidade do segundo estágio ($v_2$) forem atendidos:
| $ s = s_2 + v_2 ( t - t_2 )$ |
que representado como:
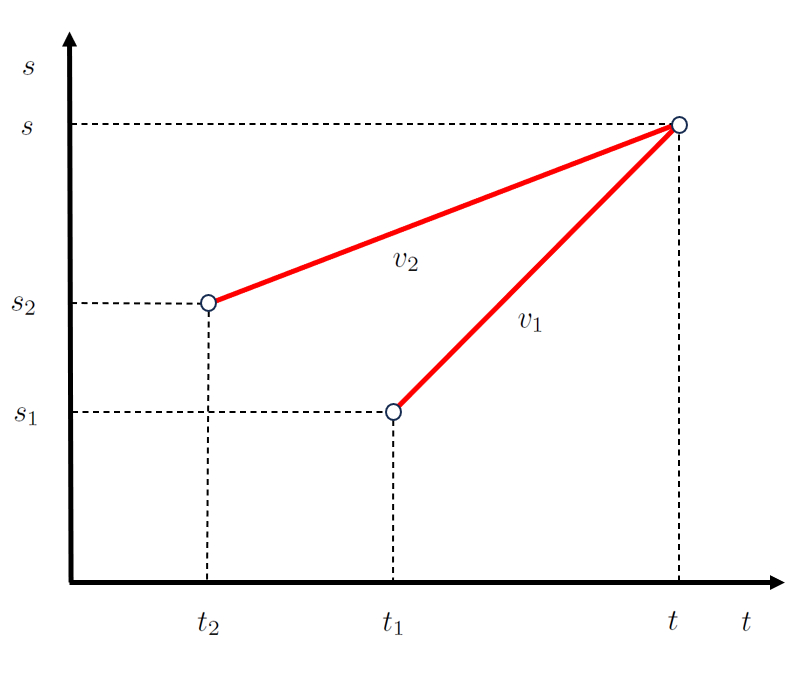
(ID 12510)
A chave que ambos os objetos se encontram em la posição de interseção ($s$) em um tempo o tempo de interseção ($t$). Para isso, o objeto 1 inicia sua jornada em la posição inicial do primeiro objeto ($s_1$) em um tempo inicial do primeiro objeto ($t_1$) com uma velocidade do primeiro estágio ($v_1$), enquanto o objeto 2 inicia sua jornada em la posição inicial do segundo objeto ($s_2$) em um tempo inicial do segundo objeto ($t_2$) com uma velocidade do segundo estágio ($v_2$). Dentro desse processo, o objeto 1 viaja uma distância percorrida pelo primeiro objeto ($\Delta s_1$) em uma tempo de percurso do primeiro objeto ($\Delta t_1$), enquanto o objeto 2 viaja uma distância percorrida pelo segundo objeto ($\Delta s_2$) em uma tempo de percurso do segundo objeto ($\Delta t_2$):
(ID 15392)
ID:(445, 0)