Interceptar a velocidad constante
Storyboard 
Los objetos pueden intersectarse cuando coinciden en posición en un mismo momento. Para lograrlo, deben desplazarse desde sus respectivos puntos de inicio con velocidades que les permitan coincidir en posición y tiempo al final del viaje.
ID:(445, 0)
Interceptar a velocidad constante
Descripción 
Los objetos pueden intersectarse cuando coinciden en posición en un mismo momento. Para lograrlo, deben desplazarse desde sus respectivos puntos de inicio con velocidades que les permitan coincidir en posición y tiempo al final del viaje.
Variables
Cálculos
Cálculos
Ecuaciones
Con la distancia recorrida en un tiempo ($\Delta s$) es con la posición ($s$) y la posición inicial ($s_0$):
| $ \Delta s = s - s_0 $ |
y el tiempo transcurrido ($\Delta t$) es con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Se tiene que la ecuaci n de la velocidad media:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
puede escribirse como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
Por lo tanto, despejando, se obtiene:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Con la distancia recorrida en un tiempo ($\Delta s$) es con la posición ($s$) y la posición inicial ($s_0$):
| $ \Delta s = s - s_0 $ |
y el tiempo transcurrido ($\Delta t$) es con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Se tiene que la ecuaci n de la velocidad media:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
puede escribirse como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
Por lo tanto, despejando, se obtiene:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Si se parte de la posición inicial ($s_0$) y se desea calcular la distancia recorrida en un tiempo ($\Delta s$), es necesario definir un valor para la posición ($s$).
En un sistema unidimensional, la distancia recorrida en un tiempo ($\Delta s$) se obtiene simplemente restando la posición inicial ($s_0$) de la posición ($s$), lo que da como resultado:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Si se parte de la posición inicial ($s_0$) y se desea calcular la distancia recorrida en un tiempo ($\Delta s$), es necesario definir un valor para la posición ($s$).
En un sistema unidimensional, la distancia recorrida en un tiempo ($\Delta s$) se obtiene simplemente restando la posición inicial ($s_0$) de la posición ($s$), lo que da como resultado:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Ejemplos
Durante el proceso de intersecci n, dos cuerpos se desplazan de manera que coincidan en la posición de la intersección ($s$) y el tiempo de intersección ($t$).
Para lograr esto, cada cuerpo debe partir de sus posiciones y tiempos iniciales, con desplazamientos de la velocidad primera etapa ($v_1$) y la velocidad primera etapa ($v_1$), respectivamente, de modo que se produzca la coincidencia.
(ID 15394)
En el caso de intercepci n se trata de dos cuerpos que se desplazan de forma que en un tiempo de intersección ($t$) coincidir n en su ERROR:10258,0.
Para este efecto cada cuerpo:
• inicia en el tiempo inicial del primer objeto ($t_1$) en la posición inicial del primer objeto ($s_1$) su desplazamiento con la velocidad primera etapa ($v_1$).
• inicia en el tiempo inicial del segundo objeto ($t_2$) en la posición inicial del segundo objeto ($s_2$) su desplazamiento con la velocidad segunda etapa ($v_2$).
que deben ser tales que se d la intersecci n.
Con ello, los diagramas de la posici n en el tiempo pueden ser acopladas como puesta la siguiente representaci n:
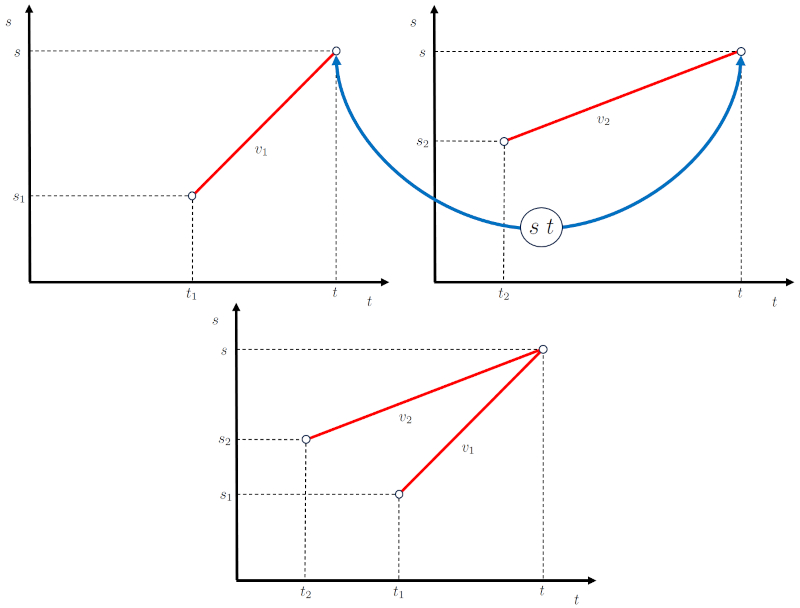
(ID 15505)
En el caso de una intersecci n o choque entre dos objetos, es com n que la velocidad primera etapa ($v_1$) y la velocidad segunda etapa ($v_2$) deban ser tales que se produzca la coincidencia.
Esto significa que la distancia recorrida por el primer objeto ($\Delta s_1$) y la duración del viaje del primer objeto ($\Delta t_1$) deben dar lugar a una velocidad primera etapa ($v_1$),
| $ v_1 \equiv\displaystyle\frac{ \Delta s_1 }{ \Delta t_1 }$ |
tal que con la distancia recorrida por el segundo objeto ($\Delta s_2$) y la duración de viaje del segundo objeto ($\Delta t_2$) se obtenga una velocidad segunda etapa ($v_2$),
| $ v_2 \equiv\displaystyle\frac{ \Delta s_2 }{ \Delta t_2 }$ |
de modo que finalmente coincidan en tiempo y espacio (posici n):
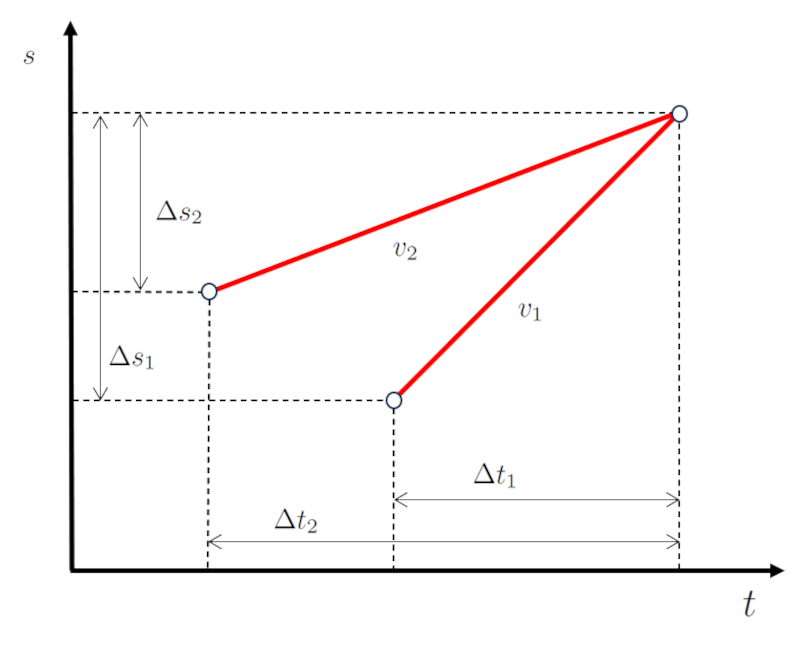
(ID 12509)
En el caso de un movimiento en el que dos objetos se interceptan, como la posición de la intersección ($s$) y el tiempo de intersección ($t$), es com n para ambos. Por lo tanto, si para el primer objeto, el tiempo inicial del primer objeto ($t_1$) y la posición inicial del primer objeto ($s_1$) con la velocidad primera etapa ($v_1$) cumplen:
| $ s = s_1 + v_1 ( t - t_1 )$ |
y para el segundo objeto, el tiempo inicial del segundo objeto ($t_2$) y la posición inicial del segundo objeto ($s_2$) con la velocidad segunda etapa ($v_2$) se cumplen:
| $ s = s_2 + v_2 ( t - t_2 )$ |
Esto se representa como:
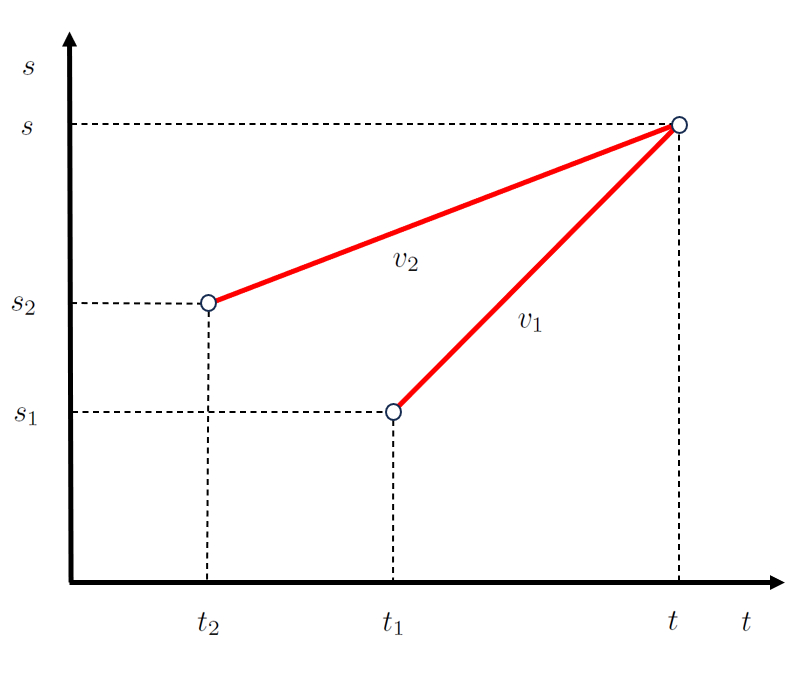
(ID 12510)
La clave es que ambos objetos se encuentren en la posición de la intersección ($s$) al mismo tiempo, el tiempo de intersección ($t$). Para lograr esto, el objeto 1 comienza su viaje en la posición inicial del primer objeto ($s_1$) a las un tiempo inicial del primer objeto ($t_1$) con una velocidad de una velocidad primera etapa ($v_1$), mientras que el objeto 2 inicia su recorrido en la posición inicial del segundo objeto ($s_2$) a las un tiempo inicial del segundo objeto ($t_2$) con una velocidad de una velocidad segunda etapa ($v_2$). En este proceso, el objeto 1 viaja una distancia recorrida por el primer objeto ($\Delta s_1$) en una duración del viaje del primer objeto ($\Delta t_1$), mientras que el objeto 2 viaja una distancia recorrida por el segundo objeto ($\Delta s_2$) en una duración de viaje del segundo objeto ($\Delta t_2$):
(ID 15392)
ID:(445, 0)
