Konstante Geschwindigkeit
Storyboard 
Um die Entwicklung der Position im Laufe der Zeit zu beschreiben, muss man die Variation dieser im Zeitverlauf untersuchen.
Die Beziehung zwischen der Veränderung der Position entspricht der zurückgelegten Strecke in der verstrichenen Zeit, die, wenn durch diese Zeit dividiert, zur Geschwindigkeit wird.
Für eine endliche vergangene Zeit entspricht die Geschwindigkeit der Durchschnittsgeschwindigkeit während dieses Intervalls.
ID:(608, 0)
Position
Bild 
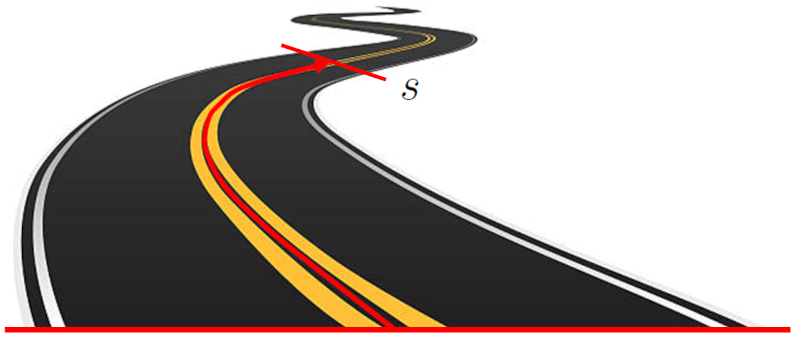
Die Position ($s$) eines Objekts in einem eindimensionalen System bezieht sich auf den Standort des Objekts in Bezug auf einen Referenzpunkt. Diese Lage wird als Entfernung zwischen dem Objekt und dem Ursprungspunkt ausgedrückt. Diese Entfernung kann eine Gerade auf einem kartesischen Koordinatensystem sein oder einem gekrümmten Pfad folgen.
ID:(15, 0)
Ausgangsposition
Notiz 
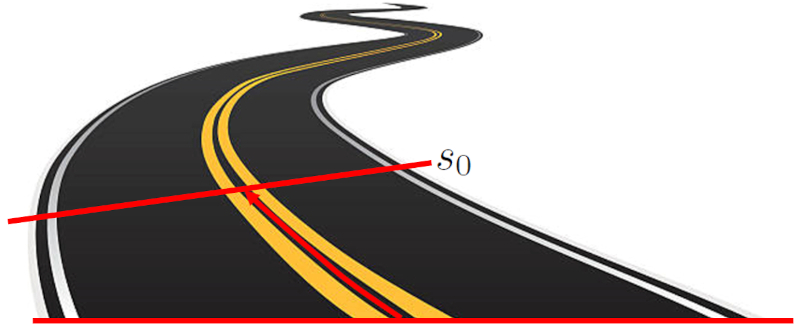
Die Ausgangsstellung ($s_0$) ist der Startort eines Objekts, bevor sich dieses bewegt. Diese Position wird als Entfernung zwischen dem Objekt und dem Ursprungspunkt definiert. Diese Entfernung kann eine Gerade auf einem kartesischen Koordinatensystem sein oder einem gekrümmten Pfad folgen.
ID:(10302, 0)
Zurückgelegte Strecke
Zitat 
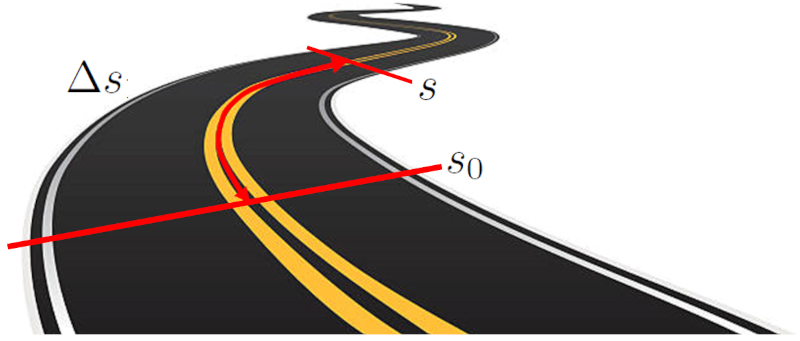
Die Zurückgelegte Strecke in einer Zeit ($\Delta s$) eines Objekts wird gemessen, indem man die Entfernung zwischen zwei spezifischen Punkten entlang einer Trajektorie misst. Diese Trajektorie kann eine Gerade auf einem kartesischen Koordinatensystem oder ein gekrümmter Pfad sein. Die Entfernung wird berechnet, indem man die Länge der Trajektorie zwischen den beiden Start- und Endpunkten misst.
ID:(9495, 0)
Geschwindigkeit als Steigung der Positionskurve
Audio 
Wenn die Verschiebung als eine Linie zwischen dem Ursprung O und dem Punkt A dargestellt wird:
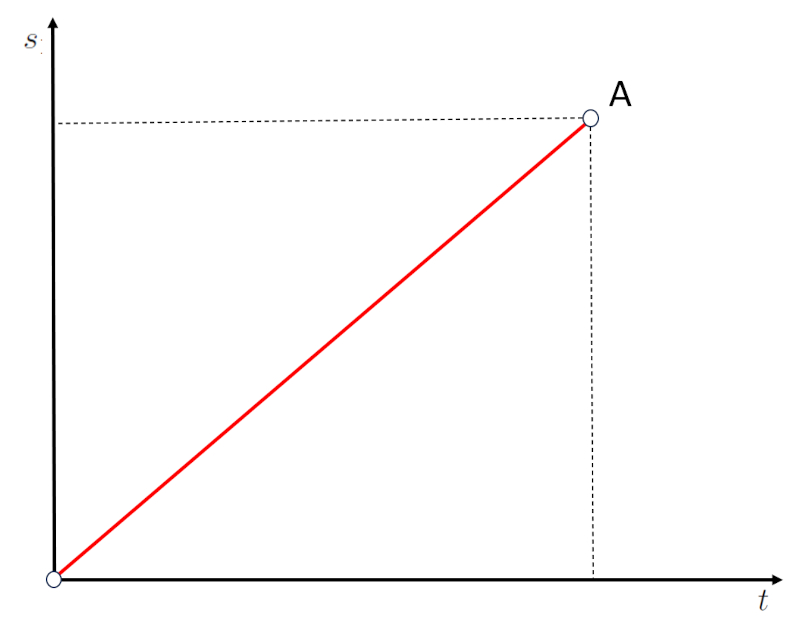
Sieht man, dass eine Strecke in einer bestimmten Zeit zurückgelegt wurde. Daher entspricht die Steigung der Grafik Strecke vs. Zeit der Geschwindigkeit.
Wenn die Steigung größer ist, bedeutet dies, dass eine Strecke in kürzerer Zeit zurückgelegt wird, was einer höheren Geschwindigkeit entspricht.
Wenn die Steigung kleiner ist, bedeutet dies, dass eine Strecke in längerer Zeit zurückgelegt wird, was einer niedrigeren Geschwindigkeit entspricht.
ID:(2239, 0)
Zeitpfaddiagramm mit horizontalem Segment
Video 
Ein zweiter Fall sind horizontale Abschnitte im Weg-Zeit-Diagramm:
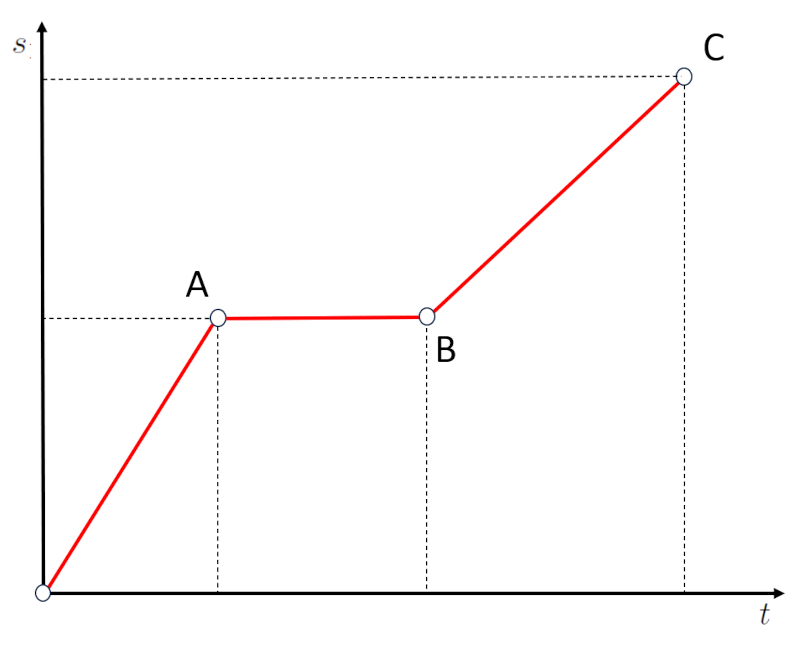
Wenn wir uns den Abschnitt AB ansehen, werden wir feststellen, dass sich der Weg trotz verstrichener Zeit nicht verändert hat. Das bedeutet, dass das Objekt angehalten ist. Daher entsprechen horizontale Abschnitte, die einer Nullsteigung entsprechen, Phasen, in denen die Geschwindigkeit null ist.
ID:(2241, 0)
Zeitpfaddiagramm für konstante Geschwindigkeit und Anfangszeit
Einheit 
Für den Fall einer konstanten Geschwindigkeit und eines Anfangszeitpunkts kann die Position mit den Werten die Position ($s$), die Ausgangsstellung ($s_0$), die Konstante Geschwindigkeit ($v_0$), der Zeit ($t$) und der Startzeit ($t_0$) mithilfe der folgenden Gleichung berechnet werden:
| $ s = s_0 + v_0 ( t - t_0 )$ |
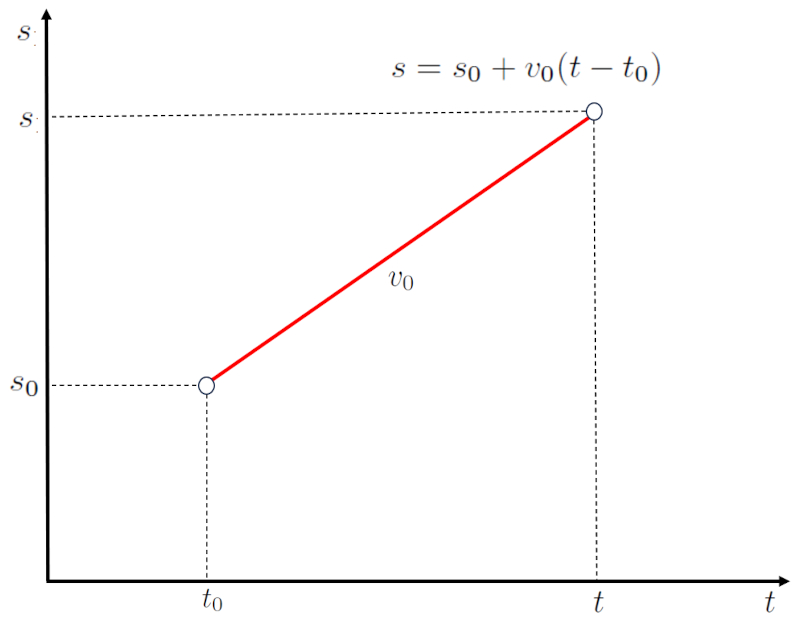
Die Gleichung entspricht einer geraden Linie mit:
• einer Steigung von die Konstante Geschwindigkeit ($v_0$)
• einem y-Achsenabschnitt bei die Ausgangsstellung ($s_0$) für der Startzeit ($t_0$)
wie unten dargestellt:
ID:(2243, 0)
Negative Steigung
Code 
Im Fall eines Graphen mit einem Abschnitt negativer Steigung:
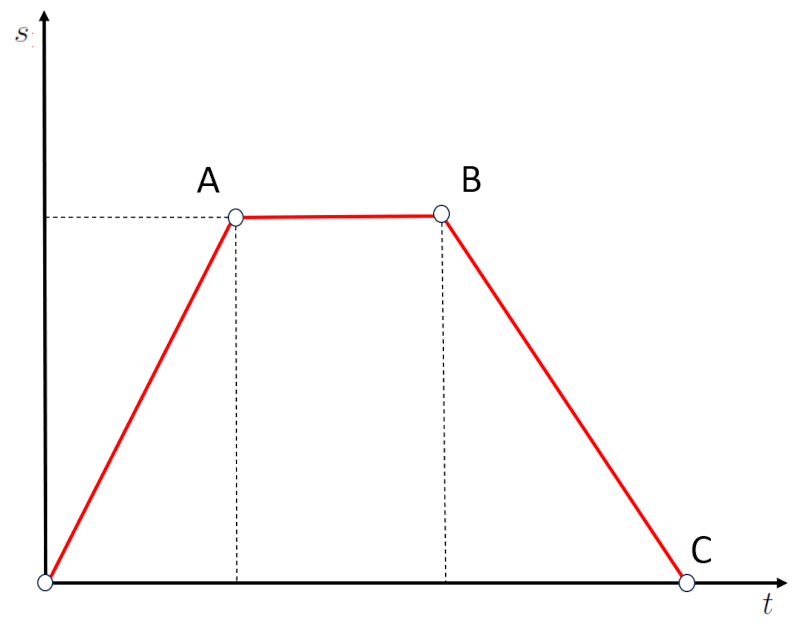
Liegt eine Situation vor, in der man von der Position B zur Position C zurückgekehrt ist, die sich in einer Entfernung von Null befindet. Mit anderen Worten, negative Steigungen bedeuten, dass man sich in die entgegengesetzte Richtung bewegt, nicht weg vom Ursprung, sondern auf ihn zu.
ID:(2245, 0)
Paradoxon des Körpers in Ruhe
Fluss 
Wenn sich ein Körper im "Ruhezustand" befindet, bedeutet dies, dass er im Ruhezustand bezüglich unseres Bezugssystems oder Koordinatensystems ist. Dieser "Ruhezustand" ist jedoch völlig relativ, das heißt, von einem Körper aus, der sich relativ zu unserem System bewegt, ist der "ruhende" Körper auch in Bewegung.
In diesem Sinne gibt es keinen "absoluten Ruhezustand", sondern nur einen relativ zum jeweiligen Bezugssystem. Deshalb ist im Allgemeinen jede Geschwindigkeitsmessung eine Messung im Verhältnis zu einem bestimmten Bezugssystem.
Wenn sich ein Körper zum Beispiel sehr langsam zu bewegen scheint, bedeutet dies nur, dass seine Geschwindigkeit der Geschwindigkeit des Bezugssystems, in dem die langsame Bewegung beobachtet wird, sehr ähnlich ist.
ID:(4405, 0)
Konstante Geschwindigkeit
Beschreibung 
Um zu beschreiben, wie sich die Position im Laufe der Zeit entwickelt, ist es notwendig, deren Veränderung über die Zeit hinweg zu analysieren.
Die Beziehung zwischen der Veränderung der Position entspricht der zurückgelegten Strecke in der verstrichenen Zeit, die, wenn man sie durch diese Zeit teilt, zur Geschwindigkeit wird.
Variablen
Berechnungen
Berechnungen
Gleichungen
Mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) gleich die Position ($s$) und die Ausgangsstellung ($s_0$):
| $ \Delta s = s - s_0 $ |
und der Abgelaufene Zeit ($\Delta t$) ist gleich der Zeit ($t$) und der Startzeit ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Die Gleichung f r die durchschnittliche Geschwindigkeit:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
kann geschrieben werden als:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
somit ergibt sich, wenn man nach ihr aufl st:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Wenn man von die Ausgangsstellung ($s_0$) ausgeht und die Zurückgelegte Strecke in einer Zeit ($\Delta s$) berechnen möchte, muss ein Wert für die Position ($s$) festgelegt werden.
In einem eindimensionalen System erhält man die Zurückgelegte Strecke in einer Zeit ($\Delta s$), indem man die Ausgangsstellung ($s_0$) von die Position ($s$) subtrahiert. Das ergibt:
| $ \Delta s = s - s_0 $ |
(ID 4352)
(ID 10276)
Beispiele
ID:(608, 0)
