Accélération instantanée
Description 
Variables
Calculs
Calculs
Équations
Comme un vecteur peut tre exprim comme un tableau de ses diff rentes composantes
$\vec{v}=(v_x,v_y,v_z)$
sa d riv e peut tre exprim e comme la d riv e de chacune de ses composantes
$\displaystyle\frac{d}{dt}\vec{v}=\displaystyle\frac{d}{dt}(v_x,v_y,v_z)=\left(\displaystyle\frac{dv_x}{dt},\displaystyle\frac{dv_y}{dt},\displaystyle\frac{dv_z}{dt}\right)=\displaystyle\frac{d\vec{v}}{dt}=\vec{a}$
en g n ral, la vitesse instantan e en plus d'une dimension est donn e par
| $ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$ |
(ID 3155)
Si l'on consid re la diff rence de a vitesse ($v$) aux temps $t+\Delta t$ et $t$ :
$\Delta v = v(t+\Delta t)-v(t)$
et que l'on prend $\Delta t$ comme le temps écoulé ($\Delta t$), alors dans la limite des temps infinit simalement courts :
$a=\displaystyle\frac{\Delta v}{\Delta t}=\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t} \rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}=\displaystyle\frac{dv}{dt}$
Cette derni re expression correspond la d riv e de la fonction a vitesse ($v$) :
| $ a =\displaystyle\frac{ d v }{ d t }$ |
qui, son tour, est la pente de la repr sentation graphique de cette fonction le temps ($t$).
(ID 4356)
Si nous int grons la d finition de a accélération instantanée ($a$) Le temps ($t$),
| $ a =\displaystyle\frac{ d v }{ d t }$ |
cela signifie que, pour un intervalle de temps $dt$, la distance parcourue est
$dv = a dt$
Si nous consid rons $N$ intervalles $dt_i$ avec des acc l rations $a_i$, le changement total de vitesse sera
$v - v_0 = \displaystyle\sum_i a_i dt_i$
Si nous consid rons la courbe de l'acc l ration en fonction du temps, les l ments $a_i dt_i$ correspondent des rectangles avec une hauteur $a_i$ et une largeur $dt_i$. La somme correspond donc l'aire sous la courbe de l'acc l ration en fonction du temps. Par cons quent, la somme peut tre exprim e comme une int grale :
| $ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $ |
(ID 10307)
tant donn que a accélération instantanée ($a$) est la d riv e de a vitesse ($v$) par rapport le temps ($t$),
| $ a =\displaystyle\frac{ d v }{ d t }$ |
et que a vitesse ($v$) est la d riv e de a position ($s$) par rapport le temps ($t$),
| $ v =\displaystyle\frac{ d s }{ d t }$ |
nous avons donc
$a=\displaystyle\frac{dv}{dt}=\displaystyle\frac{d}{dt}\displaystyle\frac{ds}{dt}=\displaystyle\frac{d^2s}{dt^2}$
ce qui implique
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
(ID 12572)
Exemples
D'un c t , il est important de diff rencier entre le cas le plus simple, unidimensionnel, et celui de plusieurs dimensions. Pour les deux cas, la d riv e de a vitesse ($v$) par rapport le temps ($t$), qui correspond la pente de la courbe de a vitesse ($v$), est gale a accélération instantanée ($a$). De mani re similaire, la d riv e de a vitesse (vector) ($\vec{v}$) par rapport le temps ($t$), qui correspond a vitesse (vector) ($\vec{v}$).
(ID 15398)
L'acc l ration est d finie comme la variation de la vitesse par temps. Cependant, ce concept se r duit une acc l ration moyenne qui existe pendant l'intervalle de temps consid r .
La limitation de l'acc l ration moyenne se refl te dans le fait qu\'un processus qui comprend un processus d\'acc l ration suivi d\'une d c l ration jusqu\' l\'arr t aura une acc l ration moyenne de z ro. Ainsi, en moyenne, il n\'y aurait pas d\'acc l ration et, s\'il est arr t , il ne se d placerait pas, alors qu\'en r alit il avance la fois dans la phase d\'acc l ration et de d c l ration.
Si nous voulons conna tre l\'acc l ration chaque instant, nous devons prendre un intervalle de temps suffisamment petit pour que pendant ce temps, l\'acc l ration puisse tre consid r e comme approximativement constante. De cette mani re, l\'acc l ration moyenne estim e de cette mani re correspond l\'acc l ration existante au moment consid r .
Par cons quent, nous parlons 'd'acc l ration instantan e' pour nous r f rer l\'acc l ration un moment donn .
(ID 11352)
Si nous prenons le temps écoulé ($\Delta t$) et observons un objet en mouvement avec la vitesse a vitesse ($v$), puis observons le m me objet un moment ult rieur $t+\Delta t$ avec la vitesse $v(t+\Delta t)$, nous pouvons estimer son acc l ration comme le changement de vitesse pendant le temps écoulé ($\Delta t$):
$a\sim\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}$
mesure que la valeur de $\Delta t$ diminue, cette expression pour l'acc l ration se rapproche du taux de variation instantan de la vitesse au moment $t$, c\'est- -dire la pente de la tangente la courbe de vitesse ce point :

Cela g n ralise le concept de a accélération instantanée ($a$) pour le cas de a accélération constante ($a_0$), comme vu pr c demment, exprim comme la d riv e de a vitesse ($v$) par rapport le temps ($t$) :
| $ a =\displaystyle\frac{ d v }{ d t }$ |
(ID 11353)
Si l'on observe que a vitesse ($v$) est gal a distance parcourue en un temps ($\Delta s$) pour le temps écoulé ($\Delta t$), cela indique que le chemin est donn par :
$\Delta s = v\Delta t$
Comme le produit $v\Delta t$ repr sente l'aire sous la courbe de vitesse par rapport au temps, qui est galement gale au chemin parcouru :

Cette aire peut galement tre calcul e avec l'int grale de la fonction correspondante. Par cons quent, l'int grale de l'acc l ration entre le temps initial ($t_0$) et le temps ($t$) correspond au changement de vitesse entre la vitesse initiale a vitesse initiale ($v_0$) et a vitesse ($v$) :
| $ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $ |
(ID 2252)
A accélération instantanée ($a$) est gal la d riv e de a vitesse ($v$) par rapport le temps ($t$) :
| $ a =\displaystyle\frac{ d v }{ d t }$ |
Et comme a vitesse ($v$) est la d riv e de a position ($s$) par rapport le temps ($t$) :
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Par cons quent, a accélération instantanée ($a$) est la deuxi me d riv e de a position ($s$) par rapport le temps ($t$),
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
ce qui correspond la courbure de la courbe a position ($s$) en fonction de le temps ($t$) :
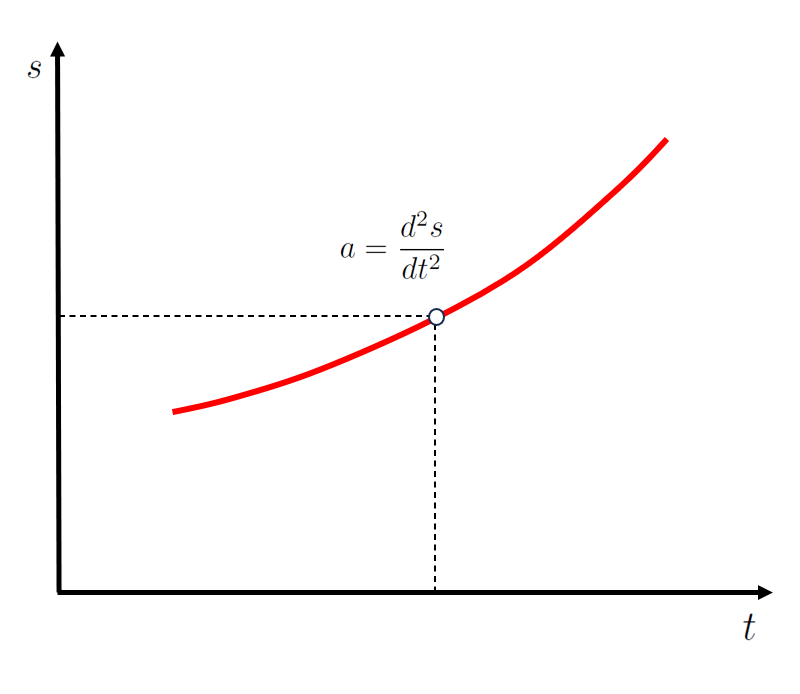
(ID 11354)
Dans le cas d'une dimension, a accélération instantanée ($a$) est li e a vitesse ($v$) par sa d riv e en le temps ($t$), tandis que l'int grale de a accélération instantanée ($a$) sur l'intervalle de le temps ($t$) Le temps initial ($t_0$) fournit a vitesse ($v$) partir de a vitesse initiale ($v_0$). Dans un contexte plus g n ral, en plus d'une dimension, la fonction a vitesse (vector) ($\vec{v}$) peut tre d riv e en le temps ($t$), ce qui donne a vitesse (vector) ($\vec{v}$).
(ID 15401)
ID:(1433, 0)
