Aceleração constante
Storyboard 
Para alcançar uma determinada velocidade, um objeto primeiro deve ter aumentado sua velocidade desde o repouso. Esse processo é chamado de aceleração e é definido em função da variação da velocidade ao longo do tempo. Por outro lado, se o objetivo for reduzir a velocidade ou até mesmo parar o objeto, também é introduzida uma aceleração, mas com o sinal oposto ao da velocidade (se tiver velocidade positiva, a aceleração é negativa e vice-versa), o que é chamado de frenagem.
ID:(609, 0)
Evolução da velocidade ao longo do tempo
Equação 
Se a velocidade for grafada como uma reta entre a velocidade em O e aquela em A:

observa-se que a velocidade aumentou ao longo do tempo transcorrido. Portanto, a inclinação do gráfico de velocidade em relação ao tempo corresponde à aceleração.
Se a inclinação for maior, isso significa que houve um aumento de velocidade em menos tempo, o que corresponde a uma maior aceleração.
Se a inclinação for menor, isso significa que houve um aumento de velocidade em mais tempo, o que corresponde a uma menor aceleração.
ID:(11346, 0)
Diagrama de tempo de velocidade com segmento horizontal
Script 
Um tipo de cenário no gráfico de velocidade vs. tempo são os segmentos horizontais:

Se observarmos o segmento AB, podemos ver que, apesar da passagem do tempo, a velocidade não mudou. Isso significa que o objeto está viajando com velocidade constante (cuidado, isso NÃO significa que tenha parado). Portanto, segmentos horizontais, que correspondem a uma inclinação zero, correspondem a estágios onde a aceleração é zero.
ID:(11348, 0)
Inclinação negativa no diagrama velocidade-tempo
Variable 
No caso do gráfico em que um segmento tem inclinação negativa:

ocorre uma situação em que a velocidade diminui entre B e C, voltando ao valor zero. Em outras palavras, inclinações negativas correspondem, neste caso, a um processo de frenagem.
Para velocidades positivas, inclinações negativas correspondem a um processo de frenagem. No entanto, para velocidades negativas, uma inclinação negativa corresponde a um aumento na velocidade negativa e, portanto, a uma aceleração. No caso de velocidades negativas, a aceleração positiva corresponde a um processo de frenagem.
Um processo de frenagem é aquele cuja aceleração tem sinal oposto ao da velocidade.
ID:(11350, 0)
Parábola de posição
Audio 
Para o caso de la aceleração constante ($a_0$), la posição ($s$) é uma função de o tempo ($t$), expressa em relação a la velocidade inicial ($v_0$), la velocidade ($s_0$) e o tempo inicial ($t_0$):
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
que corresponde a uma parábola:

A parábola é normal se a aceleração for positiva ($a_0>0$) e invertida se for negativa ($a_0<0$).
Se $v_0/a_0$ for positivo, o mínimo ($a_0>0$) ou máximo ($a_0<0$) ocorre antes do tempo inicial, então a evolução não mostrará uma mudança de sinal na velocidade, pois a inclinação da curva não muda de sinal.
Se $v_0/a_0$ for negativo, o mínimo ($a_0>0$) ou máximo ($a_0<0$) ocorre após o tempo inicial, resultando em uma inversão do movimento no futuro.
No caso de ser um mínimo ($a_0>0$), ele está localizado em uma posição abaixo da posição inicial por uma distância de $v_0^2/2a_0$. Da mesma forma, se for um máximo ($a_0<0$), estará localizado em uma posição acima da posição inicial por uma distância de $v_0^2/2a_0$.
ID:(2823, 0)
Aceleração constante
Descrição 
Para alcançar uma determinada velocidade, um objeto primeiro deve ter aumentado sua velocidade desde o repouso. Esse processo é chamado de aceleração e é definido em função da variação da velocidade ao longo do tempo. Por outro lado, se o objetivo for reduzir a velocidade ou até mesmo parar o objeto, também é introduzida uma aceleração, mas com o sinal oposto ao da velocidade (se tiver velocidade positiva, a aceleração é negativa e vice-versa), o que é chamado de frenagem.
Variáveis
Cálculos
Cálculos
Equações
No caso em que la aceleração constante ($a_0$) igual a la aceleração média ($\bar{a}$), ser igual a
| $ a_0 = \bar{a} $ |
.
Portanto, se considerarmos la diferença de velocidade ($\Delta v$) como
| $ dv \equiv v - v_0 $ |
e o tempo decorrido ($\Delta t$) como
| $ \Delta t \equiv t - t_0 $ |
,
temos que a equa o para la aceleração constante ($a_0$)
| $ a_0 \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
pode ser escrita como
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
portanto, ao rearranjarmos, obtemos
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
(ID 3156)
No caso de la aceleração constante ($a_0$), la velocidade ($v$) em fun o de o tempo ($t$) uma reta que passa por o tempo inicial ($t_0$) e la velocidade inicial ($v_0$) da forma:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Como la distância percorrida em um tempo ($\Delta s$) igual rea sob a curva velocidade-tempo, podemos somar a contribui o do ret ngulo:
$v_0(t-t_0)$
e do tri ngulo:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Com isso, obtemos com la posição ($s$) e la velocidade ($s_0$):
| $ \Delta s = s - s_0 $ |
Resultando em:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 3157)
Se resolvermos as equa es para o tempo ($t$) e o tempo inicial ($t_0$) na equa o de la velocidade ($v$), que depende de la velocidade inicial ($v_0$) e la aceleração constante ($a_0$):
| $ v = v_0 + a_0 ( t - t_0 )$ |
obtemos:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Ent o, substituindo essa express o na equa o de la posição ($s$) com la velocidade ($s_0$):
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
obtemos uma express o do caminho percorrido em fun o da velocidade:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
(ID 3158)
A defini o de la aceleração média ($\bar{a}$) considerada como a rela o entre la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$). Ou seja,
| $ dv \equiv v - v_0 $ |
e
| $ \Delta t \equiv t - t_0 $ |
A rela o entre ambos definida como la aceleração centrífuga ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
dentro desse intervalo de tempo.
(ID 3678)
Se partirmos de la velocidade ($s_0$) e quisermos calcular la distância percorrida em um tempo ($\Delta s$), é necessário definir um valor para la posição ($s$).
Em um sistema unidimensional, la distância percorrida em um tempo ($\Delta s$) é obtido simplesmente subtraindo la velocidade ($s_0$) de la posição ($s$), resultando em:
| $ \Delta s = s - s_0 $ |
(ID 4352)
(ID 4355)
Exemplos
A estrutura geral do modelo de la aceleração constante ($a_0$) tal que, por um lado, iguala-se a la aceleração média ($\bar{a}$), estabelecendo assim a rela o entre la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$).
Por outro lado, existem tr s rela es em torno de la aceleração constante ($a_0$) onde este se associa a la velocidade ($v$) e o tempo ($t$) ($v, t$), a la posição ($s$) e o tempo ($t$) ($s, t$), ou la posição ($s$) e la velocidade ($v$) ($s, v$):
Por fim, essas rela es est o associadas a par metros que n o s o mostrados, sendo eles la velocidade ($s_0$), la velocidade inicial ($v_0$) e o tempo inicial ($t_0$), e dependendo do sistema de coordenadas utilizado, podem ser definidos como nulos. Isso significa iniciar o movimento na origem ($s_0=0$), come ar a medir a partir da origem do tempo ($t_0=0$), e a origem do sistema de coordenadas estar em repouso em rela o ao observador, portanto n o h velocidade inicial ($v_0=0$).
(ID 15389)
Quando a velocidade n o constante, interessante saber como ela est aumentando / diminuindo. Para isso, importante conhecer a varia o da velocidade por unidade de tempo, o que chamamos de acelera o ou desacelera o, dependendo se um aumento ou uma diminui o dela.
Se viajarmos a uma velocidade de 100 km/h e reduzirmos a velocidade em 10 km/h a cada segundo, sabemos que vamos parar em 10 segundos.
Isso se baseia na medi o da varia o da velocidade e na varia o do tempo.
(ID 11347)
Quando a acelera o constante, a varia o da velocidade, representada por la velocidade ($v$), muda linearmente em fun o de o tempo ($t$). Isso pode ser calculado usando la velocidade inicial ($v_0$), la aceleração constante ($a_0$) e o tempo inicial ($t_0$), resultando na equa o:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Essa rela o representada graficamente como uma linha reta, conforme mostrado abaixo:

(ID 2253)
Se considerarmos uma rea de largura $\Delta t$ em um gr fico de velocidade versus tempo, isso corresponde ao caminho percorrido durante esse tempo:
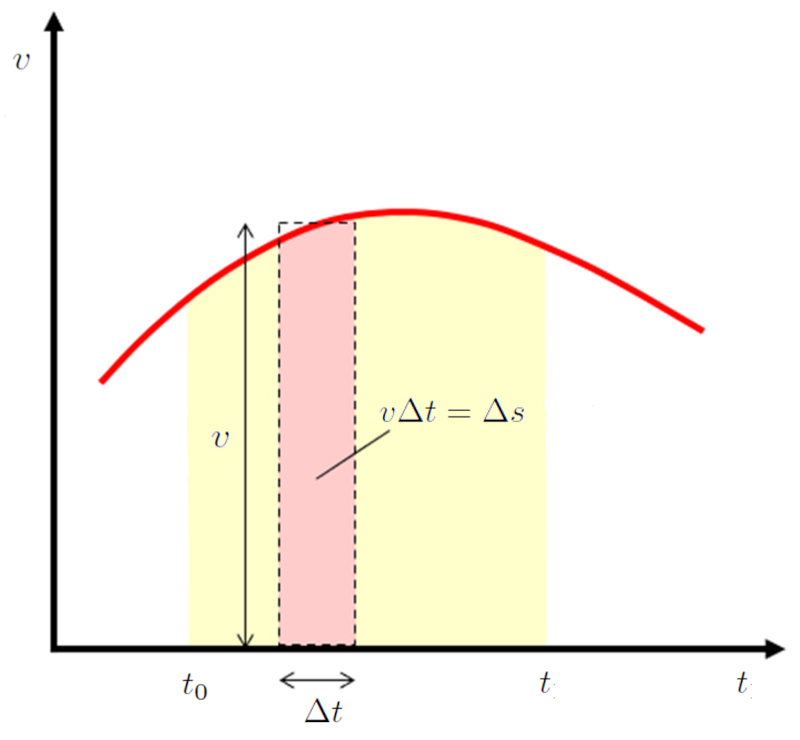
No caso particular em que a acelera o constante, a velocidade representada no gr fico de velocidade versus tempo como uma reta. Isso definido pela equa o:
| $ v = v_0 + a_0 ( t - t_0 )$ |
e graficamente representado da seguinte forma:
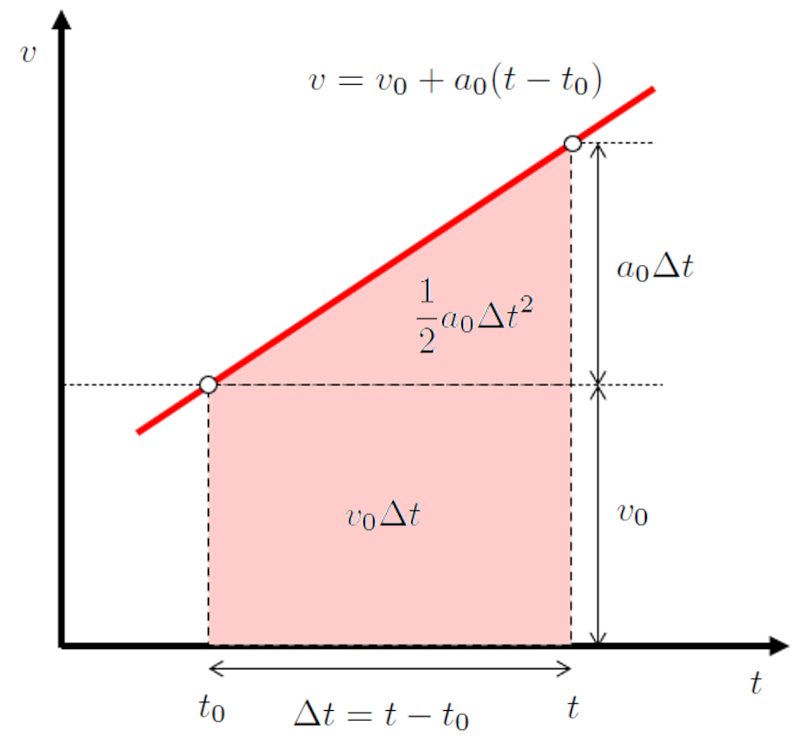
Como a rea sob a curva pode ser representada como um ret ngulo com rea
$v_0(t-t_0)$
e um tri ngulo com rea
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Portanto, o caminho percorrido, la distância percorrida em um tempo ($\Delta s$), calculado a partir de la posição ($s$) e la velocidade ($s_0$), dado por:
| $ \Delta s = s - s_0 $ |
o que significa que la posição ($s$) igual a:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 4828)
Se resolvermos a equa o de la velocidade ($v$) para la aceleração constante ($a_0$) com la velocidade inicial ($v_0$) e o tempo inicial ($t_0$):
| $ v = v_0 + a_0 ( t - t_0 )$ |
e a substituirmos na equa o de la posição ($s$) com la velocidade ($s_0$):
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
obtemos o caminho em fun o da velocidade:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
Dessa rela o, evidente que tanto o caminho de acelera o quanto o de frenagem dependem do quadrado da velocidade final/inicial. Em outras palavras, dobrar a velocidade requer um caminho quatro vezes mais longo.
(ID 14461)
Se a velocidade for grafada como uma reta entre a velocidade em O e aquela em A:

observa-se que a velocidade aumentou ao longo do tempo transcorrido. Portanto, a inclina o do gr fico de velocidade em rela o ao tempo corresponde acelera o.
Se a inclina o for maior, isso significa que houve um aumento de velocidade em menos tempo, o que corresponde a uma maior acelera o.
Se a inclina o for menor, isso significa que houve um aumento de velocidade em mais tempo, o que corresponde a uma menor acelera o.
(ID 11346)
Um tipo de cen rio no gr fico de velocidade vs. tempo s o os segmentos horizontais:

Se observarmos o segmento AB, podemos ver que, apesar da passagem do tempo, a velocidade n o mudou. Isso significa que o objeto est viajando com velocidade constante (cuidado, isso N O significa que tenha parado). Portanto, segmentos horizontais, que correspondem a uma inclina o zero, correspondem a est gios onde a acelera o zero.
(ID 11348)
No caso do gr fico em que um segmento tem inclina o negativa:

ocorre uma situa o em que a velocidade diminui entre B e C, voltando ao valor zero. Em outras palavras, inclina es negativas correspondem, neste caso, a um processo de frenagem.
Para velocidades positivas, inclina es negativas correspondem a um processo de frenagem. No entanto, para velocidades negativas, uma inclina o negativa corresponde a um aumento na velocidade negativa e, portanto, a uma acelera o. No caso de velocidades negativas, a acelera o positiva corresponde a um processo de frenagem.
Um processo de frenagem aquele cuja acelera o tem sinal oposto ao da velocidade.
(ID 11350)
Para o caso de la aceleração constante ($a_0$), la posição ($s$) uma fun o de o tempo ($t$), expressa em rela o a la velocidade inicial ($v_0$), la velocidade ($s_0$) e o tempo inicial ($t_0$):
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
que corresponde a uma par bola:

A par bola normal se a acelera o for positiva ($a_0>0$) e invertida se for negativa ($a_0<0$).
Se $v_0/a_0$ for positivo, o m nimo ($a_0>0$) ou m ximo ($a_0<0$) ocorre antes do tempo inicial, ent o a evolu o n o mostrar uma mudan a de sinal na velocidade, pois a inclina o da curva n o muda de sinal.
Se $v_0/a_0$ for negativo, o m nimo ($a_0>0$) ou m ximo ($a_0<0$) ocorre ap s o tempo inicial, resultando em uma invers o do movimento no futuro.
No caso de ser um m nimo ($a_0>0$), ele est localizado em uma posi o abaixo da posi o inicial por uma dist ncia de $v_0^2/2a_0$. Da mesma forma, se for um m ximo ($a_0<0$), estar localizado em uma posi o acima da posi o inicial por uma dist ncia de $v_0^2/2a_0$.
(ID 2823)
Uma situa o comum quando a acelera o constante, o que significa que a velocidade aumenta proporcionalmente ao tempo decorrido.
Portanto la aceleração constante ($a_0$),
$a_0=g$
Um exemplo de acelera o constante a acelera o devida gravidade experimentada por objetos que caem sobre a superf cie do planeta. Na superf cie da Terra, esta acelera o de $9,8 m/s^2$ e geralmente designada pela letra $g$. De fato, existe uma unidade de medida chamada $g$ que corresponde a $9,8 m/s^2$.
(ID 11351)
Um corpo que se desloca a uma velocidade constante n o experimenta acelera o.
Portanto, no caso em que la aceleração constante ($a_0$) nulo,
$a_0=0$
la posição ($s$), com la velocidade ($s_0$), la velocidade inicial ($v_0$), o tempo ($t$) e o tempo inicial ($t_0$),
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
reduz-se ao caso de velocidade constante:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 11349)
Se la aceleração constante ($a_0$) for igualado a la aceleração média ($\bar{a}$), a defini o de la aceleração média ($\bar{a}$) associada com la diferença de velocidade ($\Delta v$) e o tempo decorrido ($\Delta t$), e por outro lado, a linha que permite o c lculo de la velocidade ($v$) em termos de la velocidade inicial ($v_0$), o tempo ($t$) e o tempo inicial ($t_0$) considerada. Usando a rela o de velocidade, la posição ($s$) pode ser calculado com base em la velocidade ($s_0$), la velocidade inicial ($v_0$), o tempo ($t$) e o tempo inicial ($t_0$), ou com base em la velocidade ($s_0$), la velocidade ($v$) e la velocidade inicial ($v_0$). Ambas as equa es incluem la aceleração constante ($a_0$). Por fim, la distância percorrida em um tempo ($\Delta s$), o tempo decorrido ($\Delta t$) e la diferença de velocidade ($\Delta v$) s o inclu dos, nos quais o valor final subtra do do valor inicial:
(ID 15390)
ID:(609, 0)
