Accélération constante
Storyboard 
Pour qu'un objet atteigne une certaine vitesse, il doit d'abord avoir augmenté cette vitesse depuis le repos. Ce processus est appelé accélération et est défini en fonction de la variation de la vitesse dans le temps. En revanche, si l'objectif est de réduire la vitesse voire d'arrêter l'objet, une accélération est également introduite, mais avec le signe opposé à celui de la vitesse (si la vitesse est positive, l'accélération est négative et vice versa), ce qui est appelé freinage.
ID:(609, 0)
Evolution de la vitesse dans le temps
Équation 
Si on représente la vitesse comme une ligne droite entre la vitesse à l'instant O et celle à l\'instant A :

on constate que la vitesse a augmenté au fil du temps. Ainsi, la pente de la courbe vitesse vs temps correspond à l\'accélération.
Si la pente est plus grande, cela signifie qu\'il y a eu une augmentation de la vitesse en moins de temps, ce qui correspond à une accélération plus élevée.
Si la pente est plus faible, cela signifie qu\'il y a eu une augmentation de la vitesse en plus de temps, ce qui correspond à une accélération plus faible.
ID:(11346, 0)
Diagramme temporel de vitesse avec segment horizontal
Script 
Un type de scénario dans le graphique de vitesse par rapport au temps est lorsque des segments horizontaux sont présents :

Si nous observons le segment AB, nous pouvons constater que malgré l'écoulement du temps, la vitesse n\'a pas changé. Cela signifie que l\'objet se déplace avec une vitesse constante (attention, cela ne signifie PAS qu\'il s\'est arrêté). Par conséquent, les segments horizontaux, qui correspondent à une pente nulle, correspondent à des étapes où l\'accélération est nulle.
ID:(11348, 0)
Pente négative dans le diagramme de temps de vitesse
Variable 
Dans le cas du graphique où un segment a une pente négative:

on observe une situation où la vitesse diminue entre B et C, revenant à la valeur zéro. En d'autres termes, les pentes négatives correspondent, dans ce cas, à un processus de freinage.
Pour les vitesses positives, les pentes négatives correspondent à un processus de freinage. Cependant, pour les vitesses négatives, une pente négative correspond à une augmentation de la vitesse négative et donc à une accélération. Dans le cas des vitesses négatives, l\'accélération positive correspond à un processus de freinage.
Un processus de freinage est celui dont l\'accélération a un signe opposé à celui de la vitesse.
ID:(11350, 0)
Parabole de position
Audio 
Pour le cas de a accélération constante ($a_0$), a position ($s$) est une fonction de le temps ($t$), exprimée par rapport à A vitesse initiale ($v_0$), a vitesse ($s_0$) et le temps initial ($t_0$):
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
qui correspond à une parabole :

La parabole est normale si l'accélération est positive ($a_0>0$) et inversée si elle est négative ($a_0<0$).
Si $v_0/a_0$ est positif, le minimum ($a_0>0$) ou le maximum ($a_0<0$) se produit avant le temps initial, donc l'évolution ne montre pas de changement de signe dans la vitesse, car la pente de la courbe ne change pas de signe.
Si $v_0/a_0$ est négatif, le minimum ($a_0>0$) ou le maximum ($a_0<0$) se produit après le temps initial, ce qui entraîne une inversion du mouvement à l'avenir.
Dans le cas d'un minimum ($a_0>0$), il est situé en dessous de la position initiale d'une distance de $v_0^2/2a_0$. De même, s'il s'agit d'un maximum ($a_0<0$), il sera situé au-dessus de la position initiale d'une distance de $v_0^2/2a_0$.
ID:(2823, 0)
Accélération constante
Description 
Pour qu'un objet atteigne une certaine vitesse, il doit d'abord avoir augmenté cette vitesse depuis le repos. Ce processus est appelé accélération et est défini en fonction de la variation de la vitesse dans le temps. En revanche, si l'objectif est de réduire la vitesse voire d'arrêter l'objet, une accélération est également introduite, mais avec le signe opposé à celui de la vitesse (si la vitesse est positive, l'accélération est négative et vice versa), ce qui est appelé freinage.
Variables
Calculs
Calculs
Équations
Dans le cas o a accélération constante ($a_0$) est gal a accélération moyenne ($\bar{a}$), il sera gal
| $ a_0 = \bar{a} $ |
.
Ainsi, si nous consid rons a différence de vitesse ($\Delta v$) comme tant
| $ dv \equiv v - v_0 $ |
et le temps écoulé ($\Delta t$) comme tant
| $ \Delta t \equiv t - t_0 $ |
,
alors l' quation pour a accélération constante ($a_0$)
| $ a_0 \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
peut tre crite comme
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
ainsi, en isolant, nous obtenons
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
(ID 3156)
Dans le cas de a accélération constante ($a_0$), a vitesse ($v$) en fonction de le temps ($t$) est une droite passant par le temps initial ($t_0$) et a vitesse initiale ($v_0$) selon :
| $ v = v_0 + a_0 ( t - t_0 )$ |
Comme a distance parcourue en un temps ($\Delta s$) correspond l'aire sous la courbe de vitesse-temps, nous pouvons additionner la contribution du rectangle :
$v_0(t-t_0)$
et du triangle :
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Ainsi, avec a position ($s$) et a vitesse ($s_0$), nous obtenons :
| $ \Delta s = s - s_0 $ |
Ce qui donne finalement :
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 3157)
Si l'on r sout les quations pour le temps ($t$) et le temps initial ($t_0$) dans l' quation de a vitesse ($v$), qui d pend de a vitesse initiale ($v_0$) et a accélération constante ($a_0$) :
| $ v = v_0 + a_0 ( t - t_0 )$ |
nous obtenons :
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Ensuite, en rempla ant cette expression dans l' quation de a position ($s$) avec a vitesse ($s_0$) :
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
nous obtenons une expression du chemin parcouru en fonction de la vitesse :
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
(ID 3158)
La d finition de a accélération moyenne ($\bar{a}$) est consid r e comme la relation entre a différence de vitesse ($\Delta v$) et le temps écoulé ($\Delta t$). C'est- -dire,
| $ dv \equiv v - v_0 $ |
et
| $ \Delta t \equiv t - t_0 $ |
La relation entre les deux est d finie comme a accélération centrifuge ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
pendant cet intervalle de temps.
(ID 3678)
Si l’on part de a vitesse ($s_0$) et que l’on souhaite calculer a distance parcourue en un temps ($\Delta s$), il est nécessaire de définir une valeur pour a position ($s$).
Dans un système unidimensionnel, a distance parcourue en un temps ($\Delta s$) est simplement obtenu en soustrayant a vitesse ($s_0$) de a position ($s$), ce qui donne :
| $ \Delta s = s - s_0 $ |
(ID 4352)
(ID 4355)
Exemples
La structure g n rale du mod le de a accélération constante ($a_0$) est telle que, d'une part, elle s' galise a accélération moyenne ($\bar{a}$), tablissant ainsi la relation entre a différence de vitesse ($\Delta v$) et le temps écoulé ($\Delta t$).
D'autre part, il existe trois relations autour de a accélération constante ($a_0$) o celui-ci est associ a vitesse ($v$) et le temps ($t$) ($v, t$), a position ($s$) et le temps ($t$) ($s, t$), ou a position ($s$) et a vitesse ($v$) ($s, v$):
Enfin, ces relations sont associ es des param tres qui ne sont pas montr s, savoir a vitesse ($s_0$), a vitesse initiale ($v_0$) et le temps initial ($t_0$), et selon le syst me de coordonn es utilis , ils peuvent tre d finis comme nuls. Cela signifie d marrer le mouvement l'origine ($s_0=0$), commencer mesurer partir de l'origine du temps ($t_0=0$), et l'origine du syst me de coordonn es tant au repos par rapport l'observateur, il n'y a donc pas de vitesse initiale ($v_0=0$).
(ID 15389)
Lorsque la vitesse n'est pas constante, il est int ressant de savoir comment elle augmente ou diminue. Pour cela, il est important de conna tre le changement de la vitesse par unit de temps, que l\'on appelle acc l ration ou d c l ration selon qu\'il s\'agit d\'une augmentation ou d\'une diminution de celle-ci.
Si nous voyageons une vitesse de 100 km/h et que nous freinons en r duisant la vitesse de 10 km/h chaque seconde, nous savons que nous nous arr terons en 10 secondes.
Cela repose sur la mesure de la variation de la vitesse et de la variation du temps.
(ID 11347)
Lorsque l'acc l ration est constante, la variation de la vitesse, repr sent e par a vitesse ($v$), change lin airement en fonction de le temps ($t$). Cela peut tre calcul en utilisant a vitesse initiale ($v_0$), a accélération constante ($a_0$) et le temps initial ($t_0$), ce qui donne l' quation :
| $ v = v_0 + a_0 ( t - t_0 )$ |
Cette relation est repr sent e graphiquement par une ligne droite, comme illustr ci-dessous :

(ID 2253)
Si l'on consid re une zone de largeur $\Delta t$ sur un graphique de vitesse en fonction du temps, cela correspond au chemin parcouru pendant ce temps :
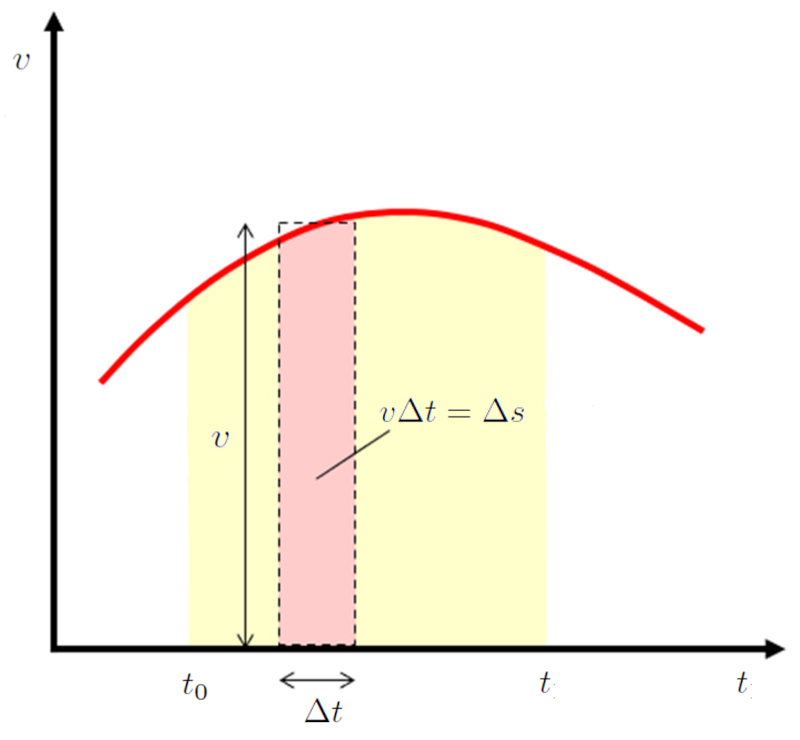
Dans le cas particulier o l'acc l ration est constante, la vitesse est repr sent e sur le graphique de vitesse en fonction du temps comme une droite. Cela est d fini par l' quation :
| $ v = v_0 + a_0 ( t - t_0 )$ |
et est repr sent graphiquement de la mani re suivante :
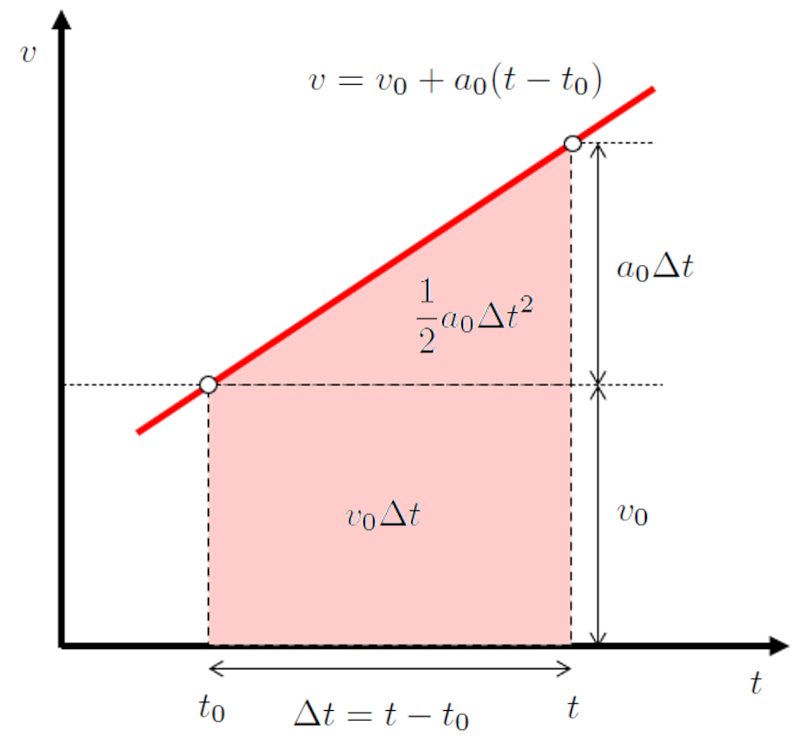
Comme l'aire sous la courbe peut tre repr sent e comme un rectangle d'aire
$v_0(t-t_0)$
et un triangle d'aire
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Ainsi, le chemin parcouru, a distance parcourue en un temps ($\Delta s$), calcul partir de a position ($s$) et a vitesse ($s_0$), est donn par :
| $ \Delta s = s - s_0 $ |
ce qui signifie que a position ($s$) est gal :
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 4828)
Si nous r solvons l' quation de a vitesse ($v$) pour a accélération constante ($a_0$) avec a vitesse initiale ($v_0$) et le temps initial ($t_0$) :
| $ v = v_0 + a_0 ( t - t_0 )$ |
et que nous rempla ons dans l' quation de a position ($s$) avec a vitesse ($s_0$) :
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
nous obtenons le chemin en fonction de la vitesse :
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
De cette relation, il appara t que tant le chemin d'acc l ration que celui de freinage d pendent du carr de la vitesse finale/initiale. En d'autres termes, doubler la vitesse n cessite un chemin quatre fois plus long.
(ID 14461)
Si on repr sente la vitesse comme une ligne droite entre la vitesse l'instant O et celle l\'instant A :

on constate que la vitesse a augment au fil du temps. Ainsi, la pente de la courbe vitesse vs temps correspond l\'acc l ration.
Si la pente est plus grande, cela signifie qu\'il y a eu une augmentation de la vitesse en moins de temps, ce qui correspond une acc l ration plus lev e.
Si la pente est plus faible, cela signifie qu\'il y a eu une augmentation de la vitesse en plus de temps, ce qui correspond une acc l ration plus faible.
(ID 11346)
Un type de sc nario dans le graphique de vitesse par rapport au temps est lorsque des segments horizontaux sont pr sents :

Si nous observons le segment AB, nous pouvons constater que malgr l' coulement du temps, la vitesse n\'a pas chang . Cela signifie que l\'objet se d place avec une vitesse constante (attention, cela ne signifie PAS qu\'il s\'est arr t ). Par cons quent, les segments horizontaux, qui correspondent une pente nulle, correspondent des tapes o l\'acc l ration est nulle.
(ID 11348)
Dans le cas du graphique o un segment a une pente n gative:

on observe une situation o la vitesse diminue entre B et C, revenant la valeur z ro. En d'autres termes, les pentes n gatives correspondent, dans ce cas, un processus de freinage.
Pour les vitesses positives, les pentes n gatives correspondent un processus de freinage. Cependant, pour les vitesses n gatives, une pente n gative correspond une augmentation de la vitesse n gative et donc une acc l ration. Dans le cas des vitesses n gatives, l\'acc l ration positive correspond un processus de freinage.
Un processus de freinage est celui dont l\'acc l ration a un signe oppos celui de la vitesse.
(ID 11350)
Pour le cas de a accélération constante ($a_0$), a position ($s$) est une fonction de le temps ($t$), exprim e par rapport a vitesse initiale ($v_0$), a vitesse ($s_0$) et le temps initial ($t_0$):
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
qui correspond une parabole :

La parabole est normale si l'acc l ration est positive ($a_0>0$) et invers e si elle est n gative ($a_0<0$).
Si $v_0/a_0$ est positif, le minimum ($a_0>0$) ou le maximum ($a_0<0$) se produit avant le temps initial, donc l' volution ne montre pas de changement de signe dans la vitesse, car la pente de la courbe ne change pas de signe.
Si $v_0/a_0$ est n gatif, le minimum ($a_0>0$) ou le maximum ($a_0<0$) se produit apr s le temps initial, ce qui entra ne une inversion du mouvement l'avenir.
Dans le cas d'un minimum ($a_0>0$), il est situ en dessous de la position initiale d'une distance de $v_0^2/2a_0$. De m me, s'il s'agit d'un maximum ($a_0<0$), il sera situ au-dessus de la position initiale d'une distance de $v_0^2/2a_0$.
(ID 2823)
Une situation courante est lorsque l'acc l ration est constante, ce qui signifie que la vitesse augmente proportionnellement au temps coul .
Par cons quent a accélération constante ($a_0$),
$a_0=g$
Un exemple d'acc l ration constante est l'acc l ration due la gravit ressentie par les objets tombant la surface de la plan te. la surface de la Terre, cette acc l ration est de $9,8 m/s^2$ et est g n ralement d sign e par la lettre $g$. En fait, il existe une unit de mesure appel e $g$ qui correspond $9,8 m/s^2$.
(ID 11351)
Un objet se d pla ant vitesse constante ne subit pas d'acc l ration.
Ainsi, dans le cas o a accélération constante ($a_0$) est nul,
$a_0=0$
a position ($s$), avec a vitesse ($s_0$), a vitesse initiale ($v_0$), le temps ($t$) et le temps initial ($t_0$),
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
se r duit au cas de vitesse constante :
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 11349)
Si a accélération constante ($a_0$) est gal a accélération moyenne ($\bar{a}$), la d finition de a accélération moyenne ($\bar{a}$) est associ e a différence de vitesse ($\Delta v$) et le temps écoulé ($\Delta t$), et d'autre part, la ligne permettant le calcul de a vitesse ($v$) en fonction de a vitesse initiale ($v_0$), le temps ($t$) et le temps initial ($t_0$) est consid r e. En utilisant la relation de vitesse, a position ($s$) peut tre calcul en fonction de a vitesse ($s_0$), a vitesse initiale ($v_0$), le temps ($t$) et le temps initial ($t_0$), ou en fonction de a vitesse ($s_0$), a vitesse ($v$) et a vitesse initiale ($v_0$). Les deux quations incluent a accélération constante ($a_0$). Enfin, a distance parcourue en un temps ($\Delta s$), le temps écoulé ($\Delta t$) et a différence de vitesse ($\Delta v$) sont inclus, dans lesquels la valeur finale est soustraite de la valeur initiale:
(ID 15390)
ID:(609, 0)
