User:
Instantaneous angular acceleration
Storyboard 
To describe how angular velocity evolves over time, one must examine its variation with respect to time.
The relationship of the change in angular velocity corresponds to the angular displacement covered over the elapsed time, which when divided by this time, yields the angular acceleration.
For an infinitesimally small time interval, the angular acceleration corresponds to the instantaneous angular acceleration.
ID:(1452, 0)
Angular Velocity as Integral of Acceleration
Note
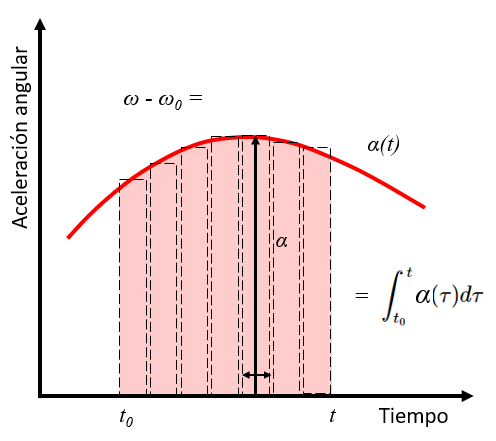
The integral of a function corresponds to the area under the curve that defines the function. Therefore, the integral of angular acceleration between the times $t_0$ and $t$ corresponds to the change in angular velocity between the initial angular velocity $\omega_0$ and $\omega$.
Thus, using angular Speed $rad/s$, initial Angular Speed $rad/s$, instantaneous Angular Acceleration $rad/s^2$, start Time $s$ and time $s$, we obtain:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
This is illustrated in the following graph:
ID:(11415, 0)
Instantaneous angular acceleration
Description
To describe how angular velocity evolves over time, one must examine its variation with respect to time. The relationship of the change in angular velocity corresponds to the angular displacement covered over the elapsed time, which when divided by this time, yields the angular acceleration. For an infinitesimally small time interval, the angular acceleration corresponds to the instantaneous angular acceleration.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Given that the tangential acceleration is
| $ a = r \alpha $ |
If the unit vector of the axis is $\hat{n}$ and the radial unit vector is $\hat{r}$, the tangential unit vector can be calculated using the cross product:
$\hat{t} = \hat{n} \times \hat{r}$
As a result, considering that
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
, and
$\vec{\alpha} = \alpha \hat{n}$
,
we can deduce that
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
which translates to
| $ \vec{a} = \vec{\alpha} \times \vec{r} $ |
.
(ID 11598)
Examples
(ID 15415)
If a time $t$ is taken with an angular velocity $\omega(t)$ and a point is observed at a future time $t+\Delta t$ with an angular velocity $\omega(t+\Delta t)$, the angular acceleration can be estimated as the variation
$\omega(t+\Delta t)-\omega(t)$
over time $\Delta t$:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
As the value of $\Delta t$ decreases, the acceleration takes on the role of the tangent to the velocity curve at that time:
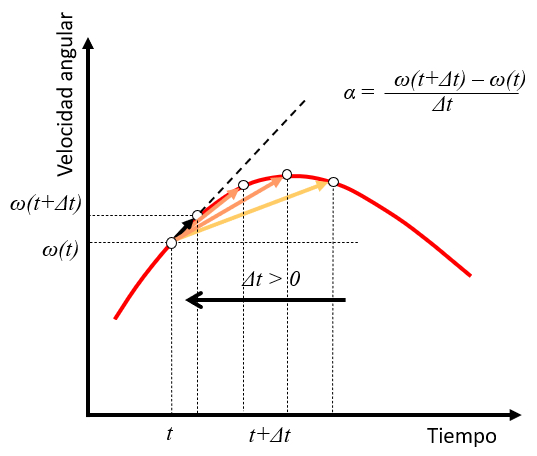
This generalizes what has already been seen for the case of constant angular acceleration.
(ID 11413)
The integral of a function corresponds to the area under the curve that defines the function. Therefore, the integral of angular acceleration between the times $t_0$ and $t$ corresponds to the change in angular velocity between the initial angular velocity $\omega_0$ and $\omega$.
Thus, using angular Speed $rad/s$, initial Angular Speed $rad/s$, instantaneous Angular Acceleration $rad/s^2$, start Time $s$ and time $s$, we obtain:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
This is illustrated in the following graph:
(ID 11415)
The orientation of tangential acceleration can be obtained using the right-hand rule, with fingers pointing towards the axis and then rotating towards the radius:
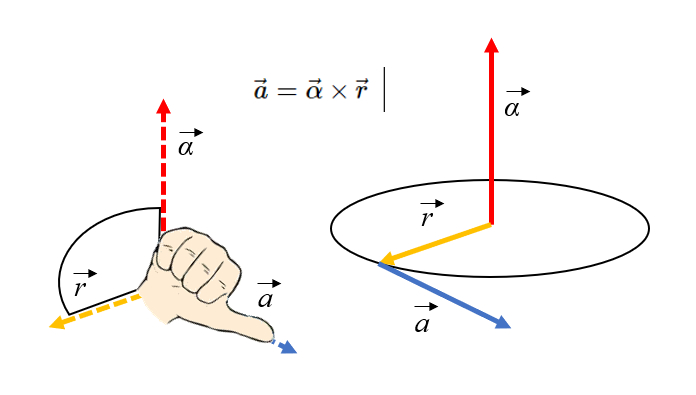
(ID 11600)
(ID 15426)
ID:(1452, 0)