Usuario:
Corrientes paralelas
Imagen 
Si permitimos que dos corrientes fluyan en forma paralela, podemos observar que surge una fuerza atractiva entre los cables.
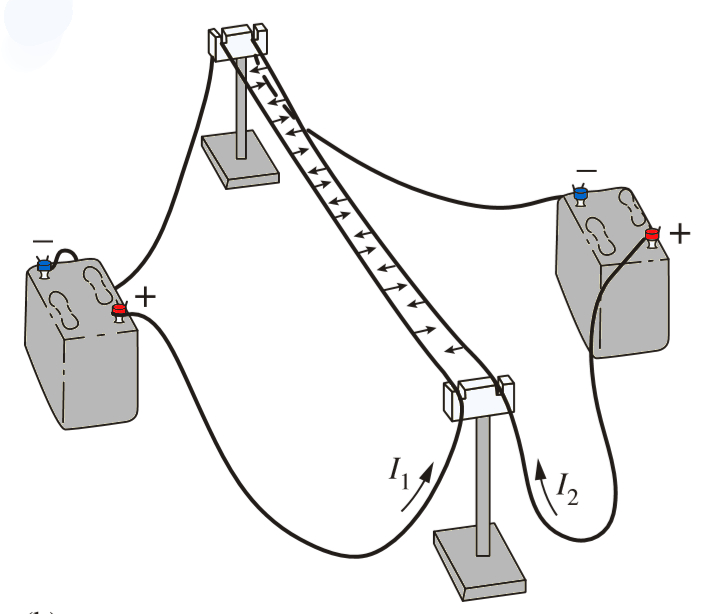
Recordemos que las corrientes están compuestas por electrones en movimiento. Naturalmente, los electrones tienden a repelerse entre sí debido a sus cargas negativas. Sin embargo, cuando estas cargas están en movimiento, esta fuerza repulsiva se convierte en una fuerza atractiva, lo que resulta en la observación de atracción entre los conductores cargados negativamente."
ID:(11772, 0)
Corrientes paralelas opuestas
Nota
Cuando permitimos que dos corrientes fluyan de forma paralela pero en direcciones opuestas, observamos una fuerza repulsiva entre los cables.
Si comparamos este experimento con aquel en el que el flujo es paralelo pero fluyen en la misma dirección, la clave radica en que en este último caso existe una velocidad relativa.
ID:(11773, 0)
Interacción de alambres
Descripción
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
(ID 12173)
Ejemplos
(ID 1933)
Una alambre por el que circula corriente genera un campo magn tico circular en torno de este.
Por ello con el campo magn tico se calcula mediante:
| $ H_w = \displaystyle\frac{ I }{ 2\pi r }$ |
(ID 12167)
Al considerar un segmento $dl$ de un alambre de una secci n $S$ y cierta longitud, se obtiene un volumen de alambre. Multiplicar este volumen por la densidad de carga $c$ nos da la cantidad de cargas contenidas en l. Finalmente, al multiplicar por la unidad de carga $q$, obtenemos la carga total presente en el segmento.
| $ \Delta Q = q c S dl $ |
(ID 12172)
La corriente se define mediante la siguiente expresi n:
| $ I =\displaystyle\frac{ \Delta Q }{ \Delta t }$ |
y las cargas en un segmento de alambre est n representadas por:
| $ \Delta Q = q c S dl $ |
El cociente entre la longitud del segmento y el intervalo de tiempo correspondiente nos da la velocidad:
$v =\displaystyle\frac{dl}{dt}$
Por lo tanto, la corriente en el alambre se puede expresar como:
| $ I = q c S v $ |
(ID 12173)
Si en un alambre por el que circula una corriente $I_1$ se genera un campo magn tico dado por:
| $ H_w = \displaystyle\frac{ I }{ 2\pi r }$ |
Este campo genera una densidad de flujo magn tico representada por:
| $ \vec{B} = \mu_0 \mu_r \vec{H}$ |
La cual a su vez produce una fuerza por segmento en un cable con una corriente $I_2$, definida como:
| $ d\vec{F} = I d\vec{l} \times \vec{B}$ |
Con esto, la fuerza por segmento se puede expresar como:
| $ \displaystyle\frac{ dF }{ dl } = \mu_0 \mu_r \displaystyle\frac{ I_1 I_2 }{2 \pi r }$ |
(ID 12169)
Si permitimos que dos corrientes fluyan en forma paralela, podemos observar que surge una fuerza atractiva entre los cables.
Recordemos que las corrientes est n compuestas por electrones en movimiento. Naturalmente, los electrones tienden a repelerse entre s debido a sus cargas negativas. Sin embargo, cuando estas cargas est n en movimiento, esta fuerza repulsiva se convierte en una fuerza atractiva, lo que resulta en la observaci n de atracci n entre los conductores cargados negativamente."
(ID 11772)
Cuando permitimos que dos corrientes fluyan de forma paralela pero en direcciones opuestas, observamos una fuerza repulsiva entre los cables.
Si comparamos este experimento con aquel en el que el flujo es paralelo pero fluyen en la misma direcci n, la clave radica en que en este ltimo caso existe una velocidad relativa.
(ID 11773)
ID:(1625, 0)