Velocidad del sonido en el mar
Storyboard 
La velocidad del sonido en el mar depende de la presión, temperatura y salinidad.
ID:(1548, 0)
Velocidad del sonido en el mar
Storyboard 
La velocidad del sonido en el mar depende de la presión, temperatura y salinidad.
Variables
Cálculos
Cálculos
Ecuaciones
Observando la imagen se nota que los senos de los angulos son respectivamente\\n\\n
$\sin\theta_i=\displaystyle\frac{c_i\Delta t}{d}$
y\\n\\n
$\sin\theta_e=\displaystyle\frac{c_e\Delta t}{d}$
\\n\\nSi se despeja en ambas ecuaciones la distancia
$d=\displaystyle\frac{c_i\Delta t}{\sin\theta_i}=\displaystyle\frac{c_e\Delta t}{\sin\theta_e}$
por lo que se tiene que
Observando la imagen se nota que los senos de los angulos son respectivamente\\n\\n
$\sin\theta_i=\displaystyle\frac{c_i\Delta t}{d}$
y\\n\\n
$\sin\theta_e=\displaystyle\frac{c_e\Delta t}{d}$
\\n\\nSi se despeja en ambas ecuaciones la distancia
$d=\displaystyle\frac{c_i\Delta t}{\sin\theta_i}=\displaystyle\frac{c_e\Delta t}{\sin\theta_e}$
por lo que se tiene que
Dado que el frecuencia del fotón ($\nu$) es el inverso de el periodo ($T$):
$\nu=\displaystyle\frac{1}{T}$
esto significa que la velocidad de la luz ($c$) es igual a la distancia recorrida en una oscilaci n, es decir, el largo de onda de luz visible ($\lambda$), dividida por el tiempo transcurrido, que corresponde al per odo:
$c=\displaystyle\frac{\lambda}{T}$
En otras palabras, tenemos la siguiente relaci n:
Dado que el frecuencia del fotón ($\nu$) es el inverso de el periodo ($T$):
$\nu=\displaystyle\frac{1}{T}$
esto significa que la velocidad de la luz ($c$) es igual a la distancia recorrida en una oscilaci n, es decir, el largo de onda de luz visible ($\lambda$), dividida por el tiempo transcurrido, que corresponde al per odo:
$c=\displaystyle\frac{\lambda}{T}$
En otras palabras, tenemos la siguiente relaci n:
Ejemplos
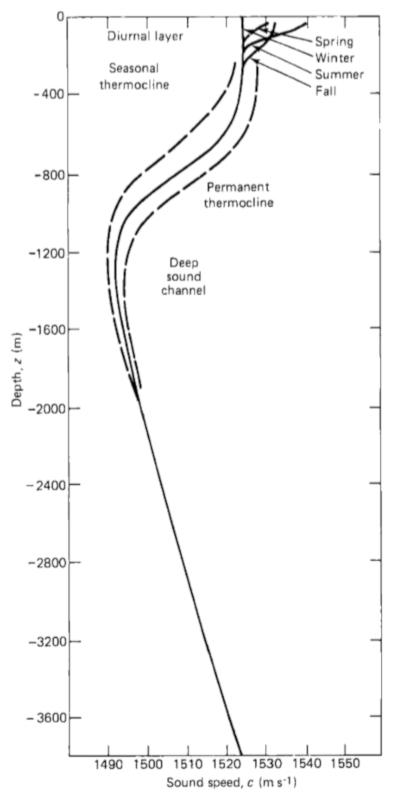
La velocidad del sonido en el oc ano varia con la profundidad seg n se muestra en la gr fica:
La forma del curva puede ir variando seg n la poca del a o.
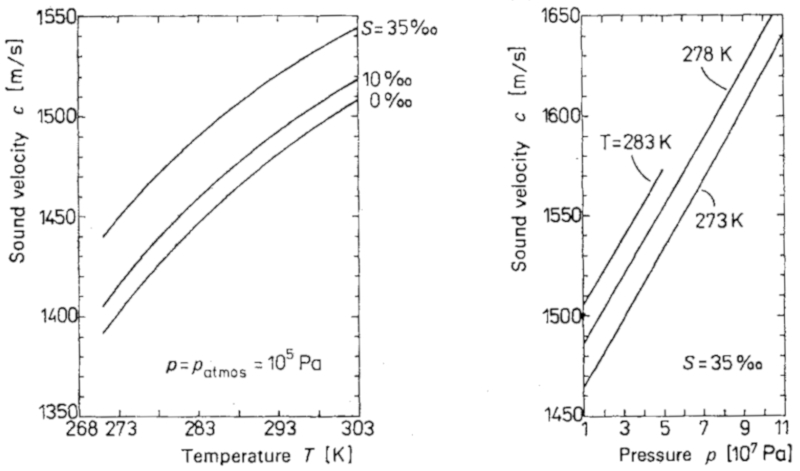
La velocidad del sonido en el oc ano depende de la temperatura y de la presi n como se muestra en la gr fica:
En 1977, Clay y Medwin desarrollaron un modelo para estimar la velocidad del sonido en funci n de la temperatura, salinidad y presi n.
Se puede estimar la velocidad del sonido ($c$) en funci n de la presión hidrostatica ($p$), la temperatura ($T$) y la salinidad ($s$) mediante la siguiente expresi n:
donde $c_i$ son constantes emp ricas.
Referencia: "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah y Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, No. 22, Noviembre 2017.
La relaci n entre los ngulos de incidencia y refractados indicados en la siguiente gr fica
se pueden escribir en funci n de la velocidad de la luz en cada medio
La relaci n entre los ngulos de incidencia y refractados indicados en la siguiente gr fica
se pueden escribir en funci n de la velocidad de la luz en cada medio
En 1977, Clay y Medwin desarrollaron un modelo para estimar la velocidad del sonido en funci n de la temperatura, salinidad y presi n.
Se puede estimar la velocidad del sonido ($c$) en funci n de la presión hidrostatica ($p$), la temperatura ($T$) y la salinidad ($s$) mediante la siguiente expresi n:
donde $c_i$ son constantes emp ricas.
Referencia: "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah y Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, No. 22, Noviembre 2017.
En 1977, Clay y Medwin desarrollaron un modelo para estimar la velocidad del sonido en funci n de la temperatura, salinidad y presi n.
Se puede estimar la velocidad del sonido ($c$) en funci n de la presión hidrostatica ($p$), la temperatura ($T$) y la salinidad ($s$) mediante la siguiente expresi n:
donde $c_i$ son constantes emp ricas.
Referencia: "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah y Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, No. 22, Noviembre 2017.
Una onda del el frecuencia del fotón ($\nu$) est relacionada con el largo de onda de luz visible ($\lambda$) a trav s de la velocidad de la luz ($c$), seg n la siguiente f rmula:
Esta f rmula corresponde a la relaci n en mec nica que establece que la velocidad de una onda es igual a su longitud de onda (espacio recorrido) dividida por el per odo de oscilaci n, o bien, directamente proporcional a la frecuencia (inversa del per odo).
Una onda del el frecuencia del fotón ($\nu$) est relacionada con el largo de onda de luz visible ($\lambda$) a trav s de la velocidad de la luz ($c$), seg n la siguiente f rmula:
Esta f rmula corresponde a la relaci n en mec nica que establece que la velocidad de una onda es igual a su longitud de onda (espacio recorrido) dividida por el per odo de oscilaci n, o bien, directamente proporcional a la frecuencia (inversa del per odo).
ID:(1548, 0)