Starten
Storyboard 
Der Schlüssel zum Abheben besteht darin, den Flügel so zu modifizieren, dass ausreichender Auftrieb bei geringeren Geschwindigkeiten erzeugt wird, um einen erfolgreichen Start auf einer gegebenen Startbahn zu ermöglichen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Auftriebskraft ($F_L$), zusammen mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$), findet sich in
Wenn wir die Oberfläche, die Auftrieb erzeugt ($S_w$) betrachten, gegeben durch die Spannweite der Flügel ($L$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$),
und f r der Koeffizient Fahrstuhl ($C_L$), definiert als
erhalten wir
Die Auftriebskraft ($F_L$) zusammen mit die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) wird durch
repr sentiert, was zusammen mit die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) gleich sein muss:
das hei t:
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
daraus ergibt sich:
Der Koeffizient Fahrstuhl ($C_L$) wird wie folgt mit die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$), die Oberfläche, die Auftrieb erzeugt ($S_w$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) berechnet:
Daher, mit die Proportionalitätskonstante Koeffizient Nachhaltigkeit ($c$) und der Anstellwinkel eines Flügels ($\alpha$),
erhalten wir
Wenn wir die Antriebskraft ($F_p$) mit die Widerstandskraft ($F_W$) mit der Gesamtobjektprofil ($S_p$), der Widerstandskoeffizient ($C_W$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) in
gleichsetzen, erhalten wir f r eine die Maximale Geschwindigkeit ($v_p$),
$F_p = \displaystyle\frac{1}{2} \rho S_w C_L v_p ^2$
was, wenn man es f r die maximale Geschwindigkeit l st, zu
f hrt.
Die Geschwindigkeit in Bezug auf das Medium ($v$) f r ein startendes Flugzeug erf llt die Gleichung mit die Maximale Beschleunigung ($a_p$), die Maximale Geschwindigkeit ($v_p$) und der Startzeit ($t$):
Durch Integration erhalten wir den folgenden Ausdruck:
$\log(v_p + v) - \log(v_p - v) - \log(v_p + v_0) + \log(v_p - v_0)= \displaystyle\frac{2 a_p}{v_p} t$
Wenn die Geschwindigkeit in Bezug auf das Medium ($v$) wesentlich kleiner ist als die Maximale Geschwindigkeit ($v_p$), k nnen die Logarithmen in eine Taylor-Reihe entwickelt werden, was zu einer N herung erster Ordnung f hrt:
Da die Geschwindigkeit in Abh ngigkeit von der Zeit durch die Gleichung
gegeben ist, k nnen wir die Geschwindigkeit als die nderungsrate der Strecke in Bezug auf die Zeit ausdr cken:
$\displaystyle\frac{ds}{dt} = \sqrt{2 a_p v_p t }$
Diese Gleichung kann integriert werden und liefert die Beziehung zwischen der zur ckgelegten Strecke und der Zeit:
Beispiele
Der Auftriebsbeiwert ist eine Funktion des Anstellwinkels und folgt in der Regel dem in der folgenden Abbildung dargestellten Trend:
Im gezeigten Fall betr gt die Steigung ungef hr 1,5 pro 15 Grad, was 0,1 1/Grad oder 5,73 1/Radiant entspricht.
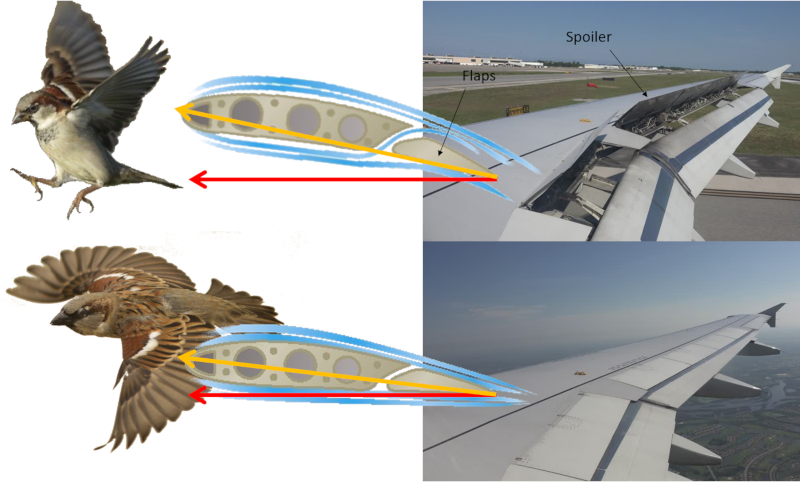
Sowohl Flugzeuge als auch V gel k nnen die Form ihrer Fl gel ndern. Flugzeuge nutzen dazu Klappen (Flaps), w hrend V gel ihre prim ren und sekund ren Federn anpassen. Auf diese Weise erreichen beide eine hohe Auftriebskraft bei niedriger Geschwindigkeit w hrend Start und Landung und einen reduzierten Auftriebsbeiwert bei hoher Geschwindigkeit.
Zus tzlich sind Flugzeuge mit Bremsklappen (Spoilern) ausgestattet, die beim Landeanflug das Abbremsen unterst tzen.
Damit ein Raumschiff oder ein Vogel in der Luft bleiben kann, muss die Erdanziehungskraft ($F_g$) die Schwerkraft ausgleichen, die durch die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) definiert ist. Mit anderen Worten, es muss sein:
Dies ist eine vereinfachte Situation, die nicht ber cksichtigt, dass der Widerstand auch eine Auftriebskraft erzeugen kann.
Um einen h heren Druck unterhalb als oberhalb des Fl gels zu erzeugen und Auftrieb zu generieren, wird das Bernoulli-Prinzip angewendet und die fehlende Energieerhaltungsdichte durch ein Koeffizient Fahrstuhl ($C_L$) korrigiert. Der Druck ber dem Fl gel, die Auftriebskraft ($F_L$), kann unter Verwendung von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) mithilfe der folgenden Formel gesch tzt werden:
Die Bedingung f r das Erreichen des Fluges wird erf llt, wenn die Auftriebskraft ($F_L$) dem Gewicht des Flugzeugs oder Vogels entspricht, das aus die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) berechnet wird. Dies wird durch ausreichende Werte von ERROR:6110,0, die Oberfläche, die Auftrieb erzeugt ($S_w$) und der Koeffizient Fahrstuhl ($C_L$) erreicht, wobei letzterer Koeffizient der anpassbare Faktor ist. Im Fall von Flugzeugen k nnen Piloten den Wert von der Koeffizient Fahrstuhl ($C_L$) mithilfe von Klappen ndern, deren Wert folgende Bedingung erf llen muss:
Die Klappen werden durch ndern des Winkels eingestellt, den der Fl gel zur Flugrichtung bildet, bekannt als Anstellwinkel.
Aus Messungen geht hervor, dass der Auftriebskoeffizient $C_L$ proportional zum Anstellwinkel $\alpha$ ist:
Nach einem bestimmten Winkel nimmt die Kurve ab und erreicht schlie lich den Wert Null. Dies liegt daran, dass ber diesem kritischen Winkel die Wirbel vollst ndig die obere Fl che des Fl gels bedecken und somit der Auftrieb verloren geht. Dieses Ph nomen wird als \"Str mungsabriss\" bezeichnet.
Da der Auftriebskoeffizient $C_L$ proportional zum Anstellwinkel $\alpha$ ist, kann der erforderliche Winkel zur Erzeugung ausreichender Auftriebskraft bei einer gegebenen Geschwindigkeit $v$ berechnet werden:
wobei $m$ die Masse, $g$ die Erdbeschleunigung, $\rho$ die Dichte des Mediums, $S_w$ die Fl gelfl che und $c$ die Proportionalit tskonstante zwischen dem Auftriebskoeffizienten und dem Anstellwinkel sind.
Wenn ein Flugzeug w hrend des Starts mit die Anzahl der Triebwerke ($n$) ein Triebwerk verliert, sinkt die Antriebskraft ($F_p$), was bedeuten k nnte, dass das Flugzeug m glicherweise nicht abheben kann und der Start abgebrochen werden muss. Ist jedoch die Geschwindigkeit in Bezug auf das Medium ($v$) h her als der neue Wert von die Maximale Geschwindigkeit ($v_p$), kann der Start sicher fortgesetzt werden. Aus diesem Grund berwacht der Pilot st ndig die Parameter und informiert den fliegenden Piloten, sobald die sogenannte die Kritische Geschwindigkeit $V2$ ($V2$), die kritische Geschwindigkeit, die wie folgt berechnet wird, berschritten ist:
Die Rotationsgeschwindigkeit $Vr$ ($Vr$) wird erreicht, wenn das Flugzeug in der Lage ist, durch die Rotation auf den erforderlichen Steigwinkel abzuheben. Mit anderen Worten, es entspricht dem Fall, in dem die Werte die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$), die Proportionalitätskonstante Koeffizient Nachhaltigkeit ($c$), die Gravitationsbeschleunigung ($g$), der Gesamtobjektprofil ($S_p$) und der Anstellwinkel eines Flügels ($\alpha$) erf llt sind:
Zu Beginn des Starts ist der aerodynamische Widerstand, der von der Geschwindigkeit abh ngt, minimal. Daher wird die Maximale Beschleunigung ($a_p$) ausschlie lich durch die Antriebskraft ($F_p$) und die Körpermasse ($m$) bestimmt:
Da der aerodynamische Widerstand beginnt, die Schubkraft zu reduzieren, wird diese anf ngliche Beschleunigung maximal sein.
Die Antriebskraft ($F_p$) wirkt die Widerstandskraft ($F_W$) entgegen, indem es Geschwindigkeit erzeugt, was wiederum die gleiche Widerstandskraft erh ht, wie in der Gesamtobjektprofil ($S_p$), der Widerstandskoeffizient ($C_W$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) in
Dieser Prozess setzt sich fort, bis der Antriebskraft die Widerstandskraft entspricht, was die maximale erreichbare Geschwindigkeit darstellt.
Indem wir die Antriebskraft mit der Widerstandskraft gleichsetzen und nach der Geschwindigkeit l sen, erhalten wir die Maximale Geschwindigkeit ($v_p$):
Da der aerodynamische Widerstand beginnt, die Antriebskraft zu reduzieren, wird diese anf ngliche Beschleunigung maximal sein.
Die Geschwindigkeit in Bezug auf das Medium ($v$) f r ein startendes Flugzeug erf llt die Gleichung mit die Maximale Beschleunigung ($a_p$), die Maximale Geschwindigkeit ($v_p$) und der Startzeit ($t$):
Wenn in der Grenze ERROR:6110,0, die viel kleiner ist als ERROR:10075,0, integriert wird, erhalten wir:
Normalerweise ist die Abhebegeschwindigkeit eines Flugzeugs deutlich niedriger als die maximale Geschwindigkeit die Maximale Geschwindigkeit ($v_p$). Daher kann die Gleichung analytisch gel st werden, wie im Verlauf erkl rt.
Da die Startgeschwindigkeit $v$ in Abh ngigkeit von der Zeit $t$ durch die Gleichung
beschrieben wird, k nnen wir die entlang der Startbahn zur ckgelegte Strecke berechnen, indem wir diese Gleichung nach der Zeit integrieren:
Andererseits k nnen wir, indem wir die erforderliche Startgeschwindigkeit ber cksichtigen, die ben tigte Zeit zur Erreichung dieser Geschwindigkeit bestimmen und unter Verwendung der zur ckgelegten Strecke die f r den Start erforderliche Startbahnl nge berechnen.
ID:(1464, 0)