Utilisateur:
La loi de Darcy
Storyboard 
La loi de Hagen-Poiseuille pour le débit total peut être reformulée en termes de différence de pression, de débit et d'un facteur pouvant être caractérisé comme une résistance hydraulique, ce qui conduit à ce que l'on connaît sous le nom de loi de Darcy.
ID:(877, 0)
Flux laminaire à travers un tube
Image
Lorsqu'un tube rempli de liquide d'une viscosité de ERROR:5422,0 est exposé à A pression en position initiale ($p_i$) en le positionner au début du tube ($L_i$) et a pression en position finale (e) ($p_e$) en le positionner au bout du tube ($L_e$), cela génère une différence de pression ($\Delta p_s$) le long de le longueur du tube ($\Delta L$), ce qui donne le profil de a vitesse dans un rayon du cylindre ($v$) :
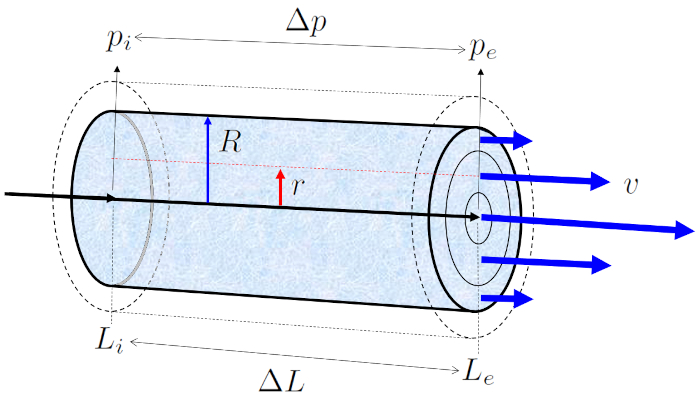
Dans les écoulements avec de faibles valeurs de le le numéro de Reynold ($Re$), où la viscosité est plus significative que l'inertie du liquide, l'écoulement se développe de manière laminée, c'est-à-dire sans la présence de turbulences.
ID:(2218, 0)
Débit selon l'équation de Hagen-Poiseuille
Noter
Le profil de a vitesse dans un rayon du cylindre ($v$) en le rayon de position dans un tube ($r$) nous permet de calculer le volumique flux ($J_V$) dans un tube en intégrant sur toute la surface, ce qui nous conduit à la loi bien connue de Hagen-Poiseuille.
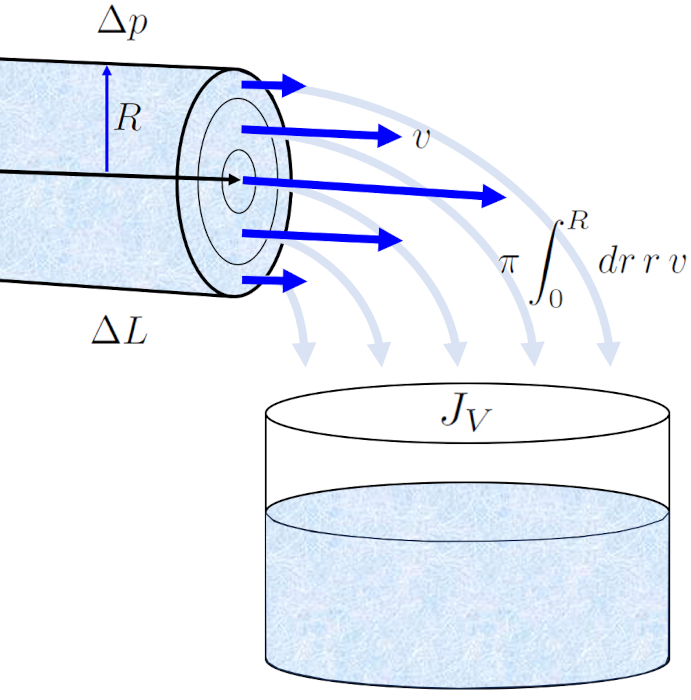
Le résultat est une équation qui dépend de ERROR:5417,0 élevé à la quatrième puissance. Cependant, il est essentiel de noter que ce profil d'écoulement n'est valable que dans le cas d'un écoulement laminaire.
Ainsi, avec cela, on déduit de a viscosité ($\eta$) que le volumique flux ($J_V$) devant un longueur du tube ($\Delta L$) et ERROR:6673,1, l'expression :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Les articles originaux qui ont donné naissance à cette loi avec un nom combiné étaient:
"Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen" (Sur les lois régissant l'écoulement de l'eau dans des récipients cylindriques), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres", Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
ID:(2216, 0)
Loi de Darcy et conductance hydraulique
Citation
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) à partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
nous pouvons introduire a conductance hydraulique ($G_h$), défini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la manière suivante :
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
pour obtenir :
| $ J_V = G_h \Delta p $ |
ID:(15723, 0)
Résistance hydraulique d'un tube
Exercer
Puisque a résistance hydraulique ($R_h$) est égal à A conductance hydraulique ($G_h$) conformément à l'équation suivante :
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
et puisque a conductance hydraulique ($G_h$) est exprimé en termes de a viscosité ($\eta$), le rayon du tube ($R$), et le longueur du tube ($\Delta L$) comme suit :
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
nous pouvons en conclure que :
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
ID:(15724, 0)
Loi de Darcy et résistance hydraulique
Équation
Le volumique flux ($J_V$) peut être calculé à partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l'équation suivante :
| $ J_V = G_h \Delta p $ |
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
on obtient :
| $ \Delta p = R_h J_V $ |
qu'Henry Darcy a formulée [1] pour modéliser le comportement général de milieux poreux plus complexes à travers lesquels un liquide s'écoule.
Le génie de cette manière de réécrire la loi de Hagen-Poiseuille réside dans le fait qu'elle montre l'analogie entre l'écoulement du courant électrique et l'écoulement du liquide. Dans ce sens, la loi de Hagen-Poiseuille correspond à la loi d'Ohm. Cela ouvre la possibilité d'appliquer les concepts des réseaux électriques aux systèmes de canalisations à travers lesquels un liquide s'écoule.
Cette loi, également connue sous le nom de loi de Darcy-Weisbach, a été publiée pour la première fois dans l'uvre de Darcy :
[1] "Les fontaines publiques de la ville de Dijon", Henry Darcy, Victor Dalmont Editeur, Paris (1856).
ID:(15720, 0)
Mesure de la loi de Darcy
Script
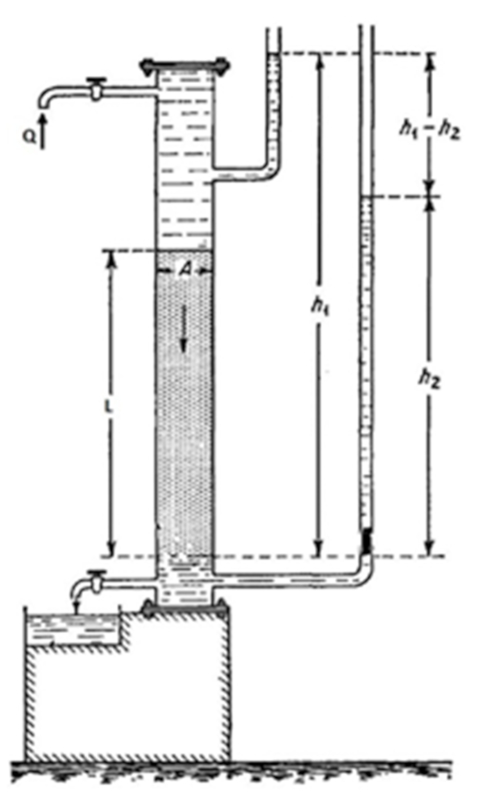
L\'expérience de Darcy comprend un cylindre rempli d\'un matériau à étudier, qui est ensuite rempli du liquide souhaité. En bas, il y a une vanne qui régule la sortie du liquide. Tant la partie supérieure que la partie inférieure ont des colonnes de liquide associées pour déterminer les pressions existantes. Ainsi, les pressions, la quantité de liquide qui s\'écoule et le temps écoulé sont mesurés, ce qui permet de déterminer la résistance hydraulique.
ID:(11104, 0)
La loi de Darcy
Storyboard
La loi de Hagen-Poiseuille pour le débit total peut être reformulée en termes de différence de pression, de débit et d'un facteur pouvant être caractérisé comme une résistance hydraulique, ce qui conduit à ce que l'on connaît sous le nom de loi de Darcy.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Si nous examinons le profil de ERROR:5449,0 pour un fluide dans un canal cylindrique, o a vitesse dans un rayon du cylindre ($v$) varie en fonction de ERROR:10120,0 selon l'expression suivante :
avec le rayon du tube ($R$) et a vitesse maximal ($v_{max}$). Nous pouvons calculer a vitesse maximal ($v_{max}$) en utilisant a viscosité ($\eta$), a différence de pression ($\Delta p$), et le longueur du tube ($\Delta L$) comme suit :
Si nous int grons la vitesse sur toute la section transversale du canal, nous obtenons le volumique flux ($J_V$), d fini comme l'int grale de $\pi r v(r)$ par rapport ERROR:10120,0 de $0$ ERROR:5417,0. Cette int grale peut tre simplifi e comme suit :
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
L'int gration donne la loi de Hagen-Poiseuille r sultante :
Le volumique flux ($J_V$) peut tre calcul partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l' quation suivante :
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
on obtient :
Puisque a résistance hydraulique ($R_h$) est gal a conductance hydraulique ($G_h$) conform ment l' quation suivante :
et puisque a conductance hydraulique ($G_h$) est exprim en termes de a viscosité ($\eta$), le rayon du tube ($R$), et le longueur du tube ($\Delta L$) comme suit :
nous pouvons en conclure que :
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
nous pouvons introduire a conductance hydraulique ($G_h$), d fini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la mani re suivante :
pour obtenir :
Exemples
Lorsqu'un tube rempli de liquide d'une viscosit de ERROR:5422,0 est expos a pression en position initiale ($p_i$) en le positionner au début du tube ($L_i$) et a pression en position finale (e) ($p_e$) en le positionner au bout du tube ($L_e$), cela g n re une différence de pression ($\Delta p_s$) le long de le longueur du tube ($\Delta L$), ce qui donne le profil de a vitesse dans un rayon du cylindre ($v$) :
Dans les coulements avec de faibles valeurs de le le numéro de Reynold ($Re$), o la viscosit est plus significative que l'inertie du liquide, l' coulement se d veloppe de mani re lamin e, c'est- -dire sans la pr sence de turbulences.
Le profil de a vitesse dans un rayon du cylindre ($v$) en le rayon de position dans un tube ($r$) nous permet de calculer le volumique flux ($J_V$) dans un tube en int grant sur toute la surface, ce qui nous conduit la loi bien connue de Hagen-Poiseuille.
Le r sultat est une quation qui d pend de ERROR:5417,0 lev la quatri me puissance. Cependant, il est essentiel de noter que ce profil d' coulement n'est valable que dans le cas d'un coulement laminaire.
Ainsi, avec cela, on d duit de a viscosité ($\eta$) que le volumique flux ($J_V$) devant un longueur du tube ($\Delta L$) et ERROR:6673,1, l'expression :
Les articles originaux qui ont donn naissance cette loi avec un nom combin taient:
"Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sur les lois r gissant l' coulement de l'eau dans des r cipients cylindriques), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres", Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
nous pouvons introduire a conductance hydraulique ($G_h$), d fini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la mani re suivante :
pour obtenir :
Puisque a résistance hydraulique ($R_h$) est gal a conductance hydraulique ($G_h$) conform ment l' quation suivante :
et puisque a conductance hydraulique ($G_h$) est exprim en termes de a viscosité ($\eta$), le rayon du tube ($R$), et le longueur du tube ($\Delta L$) comme suit :
nous pouvons en conclure que :
Le volumique flux ($J_V$) peut tre calcul partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l' quation suivante :
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
on obtient :
qu'Henry Darcy a formul e [1] pour mod liser le comportement g n ral de milieux poreux plus complexes travers lesquels un liquide s' coule.
Le g nie de cette mani re de r crire la loi de Hagen-Poiseuille r side dans le fait qu'elle montre l'analogie entre l' coulement du courant lectrique et l' coulement du liquide. Dans ce sens, la loi de Hagen-Poiseuille correspond la loi d'Ohm. Cela ouvre la possibilit d'appliquer les concepts des r seaux lectriques aux syst mes de canalisations travers lesquels un liquide s' coule.
Cette loi, galement connue sous le nom de loi de Darcy-Weisbach, a t publi e pour la premi re fois dans l'uvre de Darcy :
[1] "Les fontaines publiques de la ville de Dijon", Henry Darcy, Victor Dalmont Editeur, Paris (1856).
L\'exp rience de Darcy comprend un cylindre rempli d\'un mat riau tudier, qui est ensuite rempli du liquide souhait . En bas, il y a une vanne qui r gule la sortie du liquide. Tant la partie sup rieure que la partie inf rieure ont des colonnes de liquide associ es pour d terminer les pressions existantes. Ainsi, les pressions, la quantit de liquide qui s\' coule et le temps coul sont mesur s, ce qui permet de d terminer la r sistance hydraulique.
Le volumique flux ($J_V$) peut tre calcul avec la loi de Hagen-Poiseuille qui avec les param tres a viscosité ($\eta$), a différence de pression ($\Delta p$), le rayon du tube ($R$) et le longueur du tube ($\Delta L$) estxa0:
Avec le rayon du tube ($R$), a viscosité ($\eta$) et le longueur du tube ($\Delta L$) nous avons que une conductance hydraulique ($G_h$) vautxa0:
Avec l'introduction de a conductance hydraulique ($G_h$), nous pouvons r crire l' quation de Hagen-Poiseuille avec a différence de pression ($\Delta p$) et le volumique flux ($J_V$) l'aide de l' quation suivante :
Dans le contexte de la r sistance lectrique, son inverse existe, connu sous le nom de conductance lectrique. De mani re similaire, ce qui serait a conductance hydraulique ($G_h$) peut tre d fini en termes de a résistance hydraulique ($R_h$) travers l'expression :
Puisque a résistance hydraulique ($R_h$) est gal l'inverse de a conductance hydraulique ($G_h$), il peut tre calcul partir de l'expression de ce dernier. De cette mani re, nous pouvons identifier des param tres li s la g om trie (le longueur du tube ($\Delta L$) et le rayon du tube ($R$)) et au type de liquide (a viscosité ($\eta$)), qui peuvent tre collectivement d sign s sous le nom de une résistance hydraulique ($R_h$) :
Darcy r crit l' quation de Hagen Poiseuille de sorte que a différence de pression ($\Delta p$) soit gal a résistance hydraulique ($R_h$) fois le volumique flux ($J_V$)xa0:
ID:(877, 0)