Benützer:
Darcys Gesetz
Storyboard 
Das Hagen-Poiseuille-Gesetz für den Gesamtfluss kann in Bezug auf einen Druckunterschied, den Fluss und einen Faktor, der als hydraulischer Widerstand charakterisiert werden kann, neu definiert werden. Dies führt zur sogenannten Darcy-Gesetz.
ID:(877, 0)
Darcys Gesetz
Storyboard
Das Hagen-Poiseuille-Gesetz für den Gesamtfluss kann in Bezug auf einen Druckunterschied, den Fluss und einen Faktor, der als hydraulischer Widerstand charakterisiert werden kann, neu definiert werden. Dies führt zur sogenannten Darcy-Gesetz.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
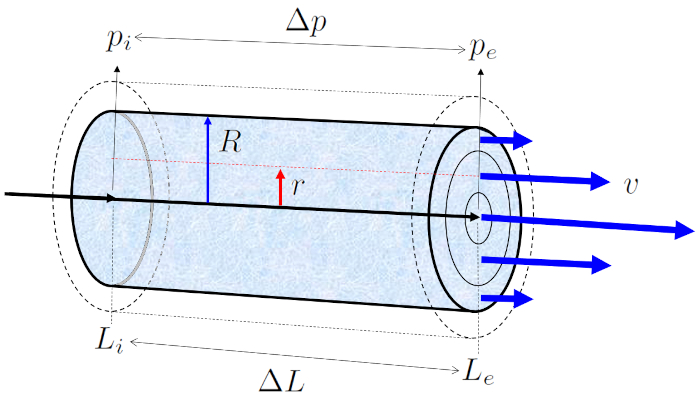
Wenn wir das Profil von ERROR:5449,0 f r ein Fluid in einem zylindrischen Kanal betrachten, in dem die Geschwindigkeit auf einer Zylinder-Radio ($v$) in Abh ngigkeit von ERROR:10120,0 gem folgendem Ausdruck variiert:
unter Verwendung von der Rohrradius ($R$) und die Maximale Durchflussrate ($v_{max}$). K nnen wir die Maximale Durchflussrate ($v_{max}$) mithilfe von die Viskosität ($\eta$), die Druckunterschied ($\Delta p$) und der Rohrlänge ($\Delta L$) wie folgt berechnen:
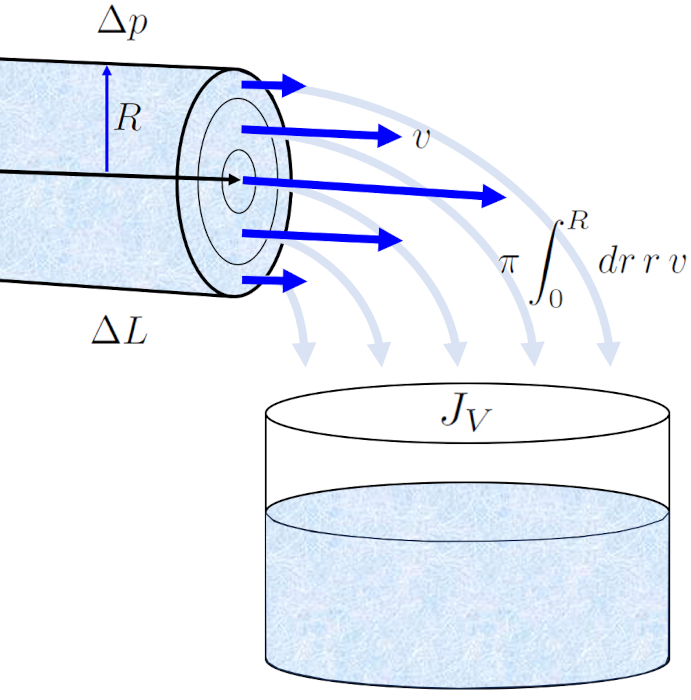
Wenn wir die Geschwindigkeit ber den Querschnitt des Kanals integrieren, erhalten wir der Volumenstrom ($J_V$), definiert als das Integral von $\pi r v(r)$ bez glich ERROR:10120,0 von $0$ bis ERROR:5417,0. Dieses Integral kann wie folgt vereinfacht werden:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
Die Integration f hrt zur resultierenden Hagen-Poiseuille-Gesetz:
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
Weiterhin, unter Verwendung der Beziehung f r die Hydraulic Resistance ($R_h$):
ergibt sich:
Da die Hydraulic Resistance ($R_h$) gem der folgenden Gleichung gleich die Hydraulische Leitfähigkeit ($G_h$) ist:
und da die Hydraulische Leitfähigkeit ($G_h$) wie folgt in Bezug auf die Viskosität ($\eta$), der Rohrradius ($R$) und der Rohrlänge ($\Delta L$) ausgedr ckt wird:
k nnen wir folgern, dass:
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns erm glicht, der Volumenstrom ($J_V$) aus der Rohrradius ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
k nnen wir die Hydraulische Leitfähigkeit ($G_h$) einf hren, das in Bezug auf der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) definiert ist:
um zu folgendem Ergebnis zu gelangen:
Beispiele
Wenn ein mit Fl ssigkeit gef lltes Rohr mit einer Viskosit t von ERROR:5422,0 Die Druck in der Ausgangsposition ($p_i$) bei der Position am Anfang des Rohres ($L_i$) und die Druck in Endlage (e) ($p_e$) bei der Positionieren am Ende des Rohres ($L_e$) ausgesetzt wird, entsteht entlang von der Rohrlänge ($\Delta L$) Eine Druckunterschied ($\Delta p_s$), was das Profil von die Geschwindigkeit auf einer Zylinder-Radio ($v$) ergibt:
Bei Str mungen mit niedrigen Werten von der Anzahl der Reynold ($Re$), wo die Viskosit t bedeutender ist als die Tr gheit der Fl ssigkeit, entwickelt sich der Fluss laminar, das hei t ohne das Vorhandensein von Turbulenzen.
Das Profil von die Geschwindigkeit auf einer Zylinder-Radio ($v$) in der Positionsradius in einem Rohr ($r$) erm glicht es uns, der Volumenstrom ($J_V$) in einem Rohr durch Integration ber die gesamte Oberfl che zu berechnen, was zur bekannten Hagen-Poiseuille-Gesetz f hrt.
Das Ergebnis ist eine Gleichung, die von ERROR:5417,0 zur vierten Potenz abh ngt. Es ist jedoch entscheidend zu beachten, dass dieses Str mungsprofil nur im Falle einer laminaren Str mung g ltig ist.
Daraus ergibt sich mit die Viskosität ($\eta$), dass der Volumenstrom ($J_V$) vor ein Rohrlänge ($\Delta L$) und eine Variación de la Presión ($\Delta p$) die Ausdruck:
Die Originalarbeiten, die zu diesem Gesetz mit einem kombinierten Namen f hrten, waren:
"Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen", Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres" (Experimentelle Untersuchungen zur Bewegung von Fl ssigkeiten in R hren mit sehr kleinen Durchmessern), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns erm glicht, der Volumenstrom ($J_V$) aus der Rohrradius ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
k nnen wir die Hydraulische Leitfähigkeit ($G_h$) einf hren, das in Bezug auf der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) definiert ist:
um zu folgendem Ergebnis zu gelangen:
Da die Hydraulic Resistance ($R_h$) gem der folgenden Gleichung gleich die Hydraulische Leitfähigkeit ($G_h$) ist:
und da die Hydraulische Leitfähigkeit ($G_h$) wie folgt in Bezug auf die Viskosität ($\eta$), der Rohrradius ($R$) und der Rohrlänge ($\Delta L$) ausgedr ckt wird:
k nnen wir folgern, dass:
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
Weiterhin, unter Verwendung der Beziehung f r die Hydraulic Resistance ($R_h$):
ergibt sich:
den Henry Darcy formuliert [1] hat, um das allgemeine Verhalten von komplexeren por sen Medien zu modellieren, durch die eine Fl ssigkeit flie t.
Die Genialit t dieser Art der Umformulierung des Hagen-Poiseuille-Gesetzes liegt darin, dass sie die Analogie zwischen dem Fluss von elektrischem Strom und dem Fluss von Fl ssigkeit zeigt. In diesem Sinne entspricht das Hagen-Poiseuille-Gesetz dem Ohm'schen Gesetz. Dies er ffnet die M glichkeit, die Konzepte elektrischer Netzwerke auf Systeme von Rohren anzuwenden, durch die eine Fl ssigkeit flie t.
Dieses Gesetz, auch als das Darcy-Weisbach-Gesetz bekannt, wurde erstmals in Darcys Werk ver ffentlicht:
[1] "Les fontaines publiques de la ville de Dijon" (Die ffentlichen Brunnen der Stadt Dijon), Henry Darcy, Victor Dalmont Editeur, Paris (1856).
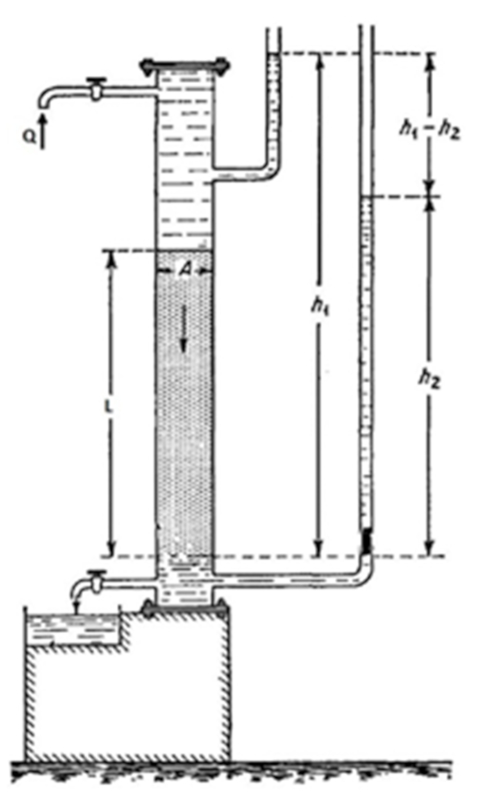
Das Darcy-Experiment umfasst einen Zylinder mit einem zu untersuchenden Material, der mit der gew nschten Fl ssigkeit gef llt wird. Im unteren Teil befindet sich ein Ventil, um den Fl ssigkeitsauslass zu regulieren. Sowohl der obere als auch der untere Teil haben zugeh rige Fl ssigkeitss ulen, um die vorhandenen Dr cke zu bestimmen. Auf diese Weise werden die Dr cke, die Menge der abflie enden Fl ssigkeit und die verstrichene Zeit gemessen, woraus der hydraulische Widerstand bestimmt werden kann.
Der Volumenstrom ($J_V$) l sst sich mit dem Hagen-Poiseuille-Gesetz berechnen, das mit den Parametern die Viskosität ($\eta$), die Druckunterschied ($\Delta p$), der Rohrradius ($R$) und der Rohrlänge ($\Delta L$) lautet:
Mit der Rohrradius ($R$), die Viskosität ($\eta$) und der Rohrlänge ($\Delta L$) haben wir, dass eine Hydraulische Leitfähigkeit ($G_h$) ist:
Durch die Einf hrung von die Hydraulische Leitfähigkeit ($G_h$) k nnen wir die Hagen-Poiseuille-Gleichung mit die Druckunterschied ($\Delta p$) und der Volumenstrom ($J_V$) mithilfe der folgenden Gleichung umschreiben:
Im Zusammenhang mit dem elektrischen Widerstand gibt es dessen Inverses, das als elektrische Leitf higkeit bekannt ist. Ebenso kann das, was die Hydraulische Leitfähigkeit ($G_h$) w re, in Bezug auf die Hydraulic Resistance ($R_h$) durch den Ausdruck definiert werden:
Da die Hydraulic Resistance ($R_h$) dem Kehrwert von die Hydraulische Leitfähigkeit ($G_h$) entspricht, kann es aus dem Ausdruck des letzteren berechnet werden. Auf diese Weise k nnen wir Parameter identifizieren, die mit der Geometrie (der Rohrlänge ($\Delta L$) und der Rohrradius ($R$)) und der Art des Fluids (die Viskosität ($\eta$)) zusammenh ngen und die gemeinsam als eine Hydraulic Resistance ($R_h$) bezeichnet werden k nnen:
Darcy schreibt die Hagen-Poiseuille-Gleichung so um, dass die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) mal der Volumenstrom ($J_V$) ist:
ID:(877, 0)
