Storyboard

El rotor del campo eléctrico busca detectar si existe circulación en este. Circulación significaría que existían lineas de campo cerradas, que sin existir cargas en el espacio se cierran sobre si mismo. Una partícula en dicho campo realizaría un camino cerrado sin escapar ni caer en o a alguna carga. Para el caso estático se muestra que no existe tal circulación y que todas las lineas de campo se inician y terminan en cargas.

>Modelo

ID:(1569, 0)

Imagen

Cuando se estableció el potencial eléctrico se trabajo con la idea de caminos entre dos puntos que en el caso de ser serrados eran nulos:

Dichos caminos se pueden segmentar en caminos mas pequeños:

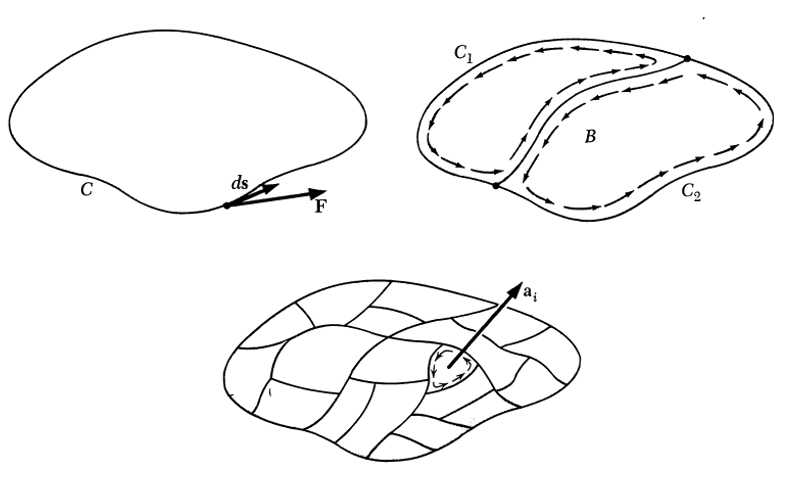
ID:(11569, 0)

Descripción

El rotor del campo eléctrico busca detectar si existe circulación en este. Circulación significaría que existían lineas de campo cerradas, que sin existir cargas en el espacio se cierran sobre si mismo. Una partícula en dicho campo realizaría un camino cerrado sin escapar ni caer en o a alguna carga. Para el caso estático se muestra que no existe tal circulación y que todas las lineas de campo se inician y terminan en cargas.

Variables

$E$

E

Campo eléctrico

V/m

$\vec{E}$

&E

Campo eléctrico

V/m

$\Gamma$

Gamma

Circulación del campo eléctrico

V

$\vec{\nabla}$

div

Divergencia

1/m

$d\vec{s}$

d&s

Elemento de largo (vector)

m

$d\vec{s}_i$

d&s_i

Elemento de largo en torno a la celda $i$

m

$dS$

dS

Elemento de superficie

m^2

$rot$

rot

Rotor

1/m

$S_i$

S_i

Superficie i

m^2

$\hat{n}_i$

&n_i

Versor normal a la superficie i

-

Cálculos

• Método alternativo
• Método tradicional
• Estrategia
• 2D
• 3D

Ecuación

Número

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 

---

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar

Ecuaciones

Ejemplos