Benützer:


Elektrischer Feldrotor
Storyboard

Der elektrische Feldrotor versucht zu erkennen, ob sich in ihm Zirkulation befindet. Zirkulation würde bedeuten, dass geschlossene Feldlinien existieren, die sich ohne vorhandene Ladungen im Raum selbst schließen. Ein Partikel in diesem Feld würde einen geschlossenen Pfad bilden, ohne zu entkommen oder auf eine Last zu fallen. Für den statischen Fall wird gezeigt, dass es keine solche Zirkulation gibt und dass alle Feldlinien in Lasten beginnen und enden.

>Modell

ID:(1569, 0)


Kreislauf
Definition

Cuando se estableció el potencial eléctrico se trabajo con la idea de caminos entre dos puntos que en el caso de ser serrados eran nulos:

$ \Delta\varphi = -\displaystyle\int_C \vec{E}\cdot d\vec{s} $



Dichos caminos se pueden segmentar en caminos mas pequeños:

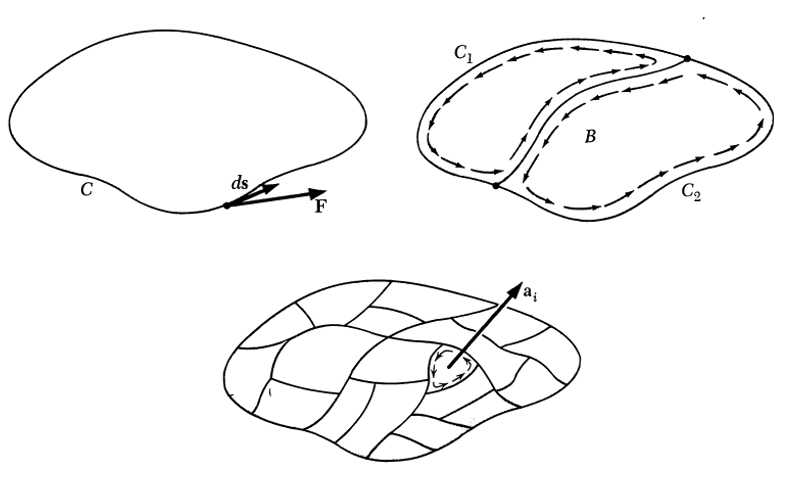
ID:(11569, 0)


Elektrischer Feldrotor
Beschreibung

Der elektrische Feldrotor versucht zu erkennen, ob sich in ihm Zirkulation befindet. Zirkulation würde bedeuten, dass geschlossene Feldlinien existieren, die sich ohne vorhandene Ladungen im Raum selbst schließen. Ein Partikel in diesem Feld würde einen geschlossenen Pfad bilden, ohne zu entkommen oder auf eine Last zu fallen. Für den statischen Fall wird gezeigt, dass es keine solche Zirkulation gibt und dass alle Feldlinien in Lasten beginnen und enden.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$\vec{\nabla}$
div
Divergenz
1/m
$\Gamma$
Gamma
Elektrische Feldzirkulation
V
$E$
E
Elektrisches Feld
V/m
$\vec{E}$
&E
Elektrisches Feld
V/m
$d\vec{s}_i$
d&s_i
Langes Element um die Zelle $i$
m
$d\vec{s}$
d&s
Längen Element (Vektor)
m
$S_i$
S_i
Oberfläche i
m^2
$dS$
dS
Oberflächenelement
m^2
$rot$
rot
Rotor
1/m
$\hat{n}_i$
&n_i
Versor normal zur Oberfläche i
-

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Beispiele

Cuando se estableci el potencial el ctrico se trabajo con la idea de caminos entre dos puntos que en el caso de ser serrados eran nulos:

$ \Delta\varphi = -\displaystyle\int_C \vec{E}\cdot d\vec{s} $



Dichos caminos se pueden segmentar en caminos mas peque os:

(ID 11569)

En base al integral a lo largo de un camino se puede definir la circulaci n como

$ \Gamma = \displaystyle\int_C \vec{E}\cdot d\vec{s}$

(ID 11570)

Una circulaci n general

$ \Gamma = \displaystyle\int_C \vec{E}\cdot d\vec{s}$



puede ser descompuesta en circulaciones menores

$\displaystyle\int_C \vec{E}\cdot d\vec{s} = \displaystyle\sum_i \displaystyle\int_{C_i} \vec{E}\cdot d\vec{s}_i$

(ID 11571)

An logo a la definici n de la divergencia

$\nabla\cdot\vec{E} = \lim_{V_i\rightarrow 0} \displaystyle\frac{1}{V_i}\displaystyle\int_{S_i} \vec{E}\cdot d\vec{S}_i$



se puede definir como el rotor la circulaci n por rea en la direcci n de la normal a la superficie

$ (\nabla\times\vec{E})\cdot\hat{n} = \lim_{S_i\rightarrow 0}\displaystyle\frac{1}{ S_i }\displaystyle\int_{C_i}\vec{E}\cdot d\vec{s}$

(ID 11572)

Con la definici n del rotor

$ (\nabla\times\vec{E})\cdot\hat{n} = \lim_{S_i\rightarrow 0}\displaystyle\frac{1}{ S_i }\displaystyle\int_{C_i}\vec{E}\cdot d\vec{s}$



se tiene que la suma sobre las superficies es

\displaystyle\int_C\vec{E}\cdot d\vec{s}=\displaystyle\sum_i S_i(
abla\times\vec{E})\cdot d\vec{S}=\displaystyle\int_S (
abla\times\vec{E})\cdot d\vec{S}

que corresponde al teorema de Stokes

$ \displaystyle\int_C \vec{E} \cdot d\vec{s} =\displaystyle\int_S (\nabla\times\vec{E} )\cdot d\vec{S} $

(ID 11573)

Da die Auflage auf einer gesperrten Stra e null ist

$ \displaystyle\oint_C \vec{E}\cdot d\vec{s}=0$



Satz von Stokes

$ \displaystyle\int_C \vec{E} \cdot d\vec{s} =\displaystyle\int_S (\nabla\times\vec{E} )\cdot d\vec{S} $



impliziert das

$ \nabla\times\vec{E} = 0 $



Dies bedeutet, dass im Falle der Elektrostatik das elektrische Feld keine Zirkulation hat, dh seine Linien bilden keine geschlossenen Kreise, ohne Ladungen zu ber hren.

(ID 11574)

ID:(1569, 0)