Usuario:


Gradiente del potencial
Storyboard

Un gradiente es un vector que se construye para una función que indica la dirección e inclinación que presenta la función en todo punto. En particular el gradiente del potencial eléctrico es igual a menos el campo eléctrico.

>Modelo

ID:(1568, 0)


Gradiente de una función
Definición

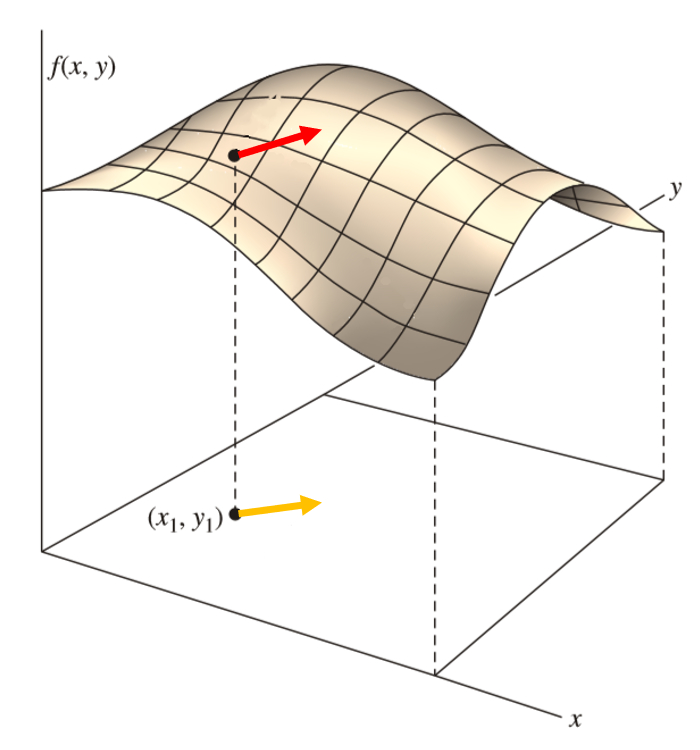
El gradiente es un vector calculado para una función que apunta a un máximo/mínimo próximo al punto en que se esta considerando.

ID:(11555, 0)


Gradiente en una dimensión
Imagen

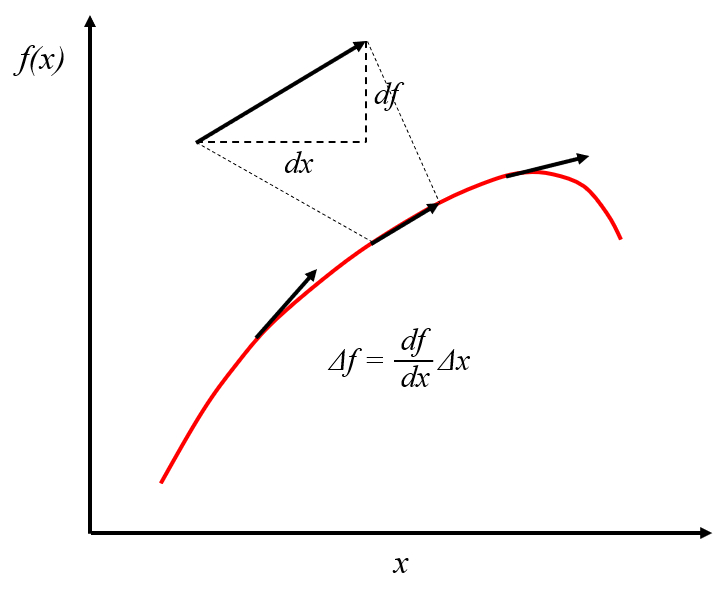
El gradiente es un vector calculado para una función que apunta a un máximo/mínimo próximo al punto en que se esta considerando. En el caso de una dimensión esto coincide con la pendiente de la curva:

ID:(11558, 0)


Gradiente en dos dimensiones
Nota

Si consideramos un punto (x,y) y observamos nuestro entrono podremos ver que la función del potencial \varphi varia tanto en la dirección \hat{x} como \hat{y}. Si nos desplazamos una distancia \Delta x en la dirección \hat{x}, veremos que su valor cambia de a\varphi(x,y) a \varphi(x+\Delta x,y). De igual forma lo hará en la dirección \hat{y} de un valor \varphi(x,y) a \varphi(x,y+\Delta y). En cada dirección existirá una pendiente

\partial_x\varphi =\displaystyle\frac{\varphi(x+\Delta x,y)-\varphi(x,y)}{\Delta x}

y

\partial_y\varphi =\displaystyle\frac{\varphi(x,y+\Delta y)-\varphi(x,y)}{\Delta y}

lo que se muestra en el diagrama:

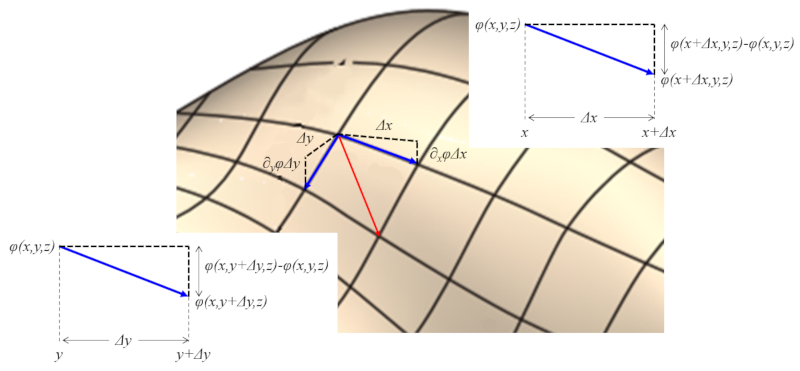
Importante es hacer notar que estudiamos las pendientes en forma independiente. O sea vimos como variaban en x sin considerar cambios en y y viceversa. Las pendientes asi calculadas también corresponden a derivadas pero con la restricción de mantener todas las variables restantes fijas se denominan derivadas parciales. La noimenclatura que se usa es

\partial_x\varphi =\displaystyle\frac{\partial\varphi}{\partial x}

\partial_y\varphi =\displaystyle\frac{\partial\varphi}{\partial y}

Por ello cada vez que veamos una delta del tipo \partial pensemos en una diferencia que no considera variaciones en otras variables. En función de no complicarse con calculo vamos a asumir simplemente que son pendientes calculadas en forma independiente de las demás direcciones y explorar el sentido físico y no matemático.

ID:(11605, 0)


Variación total
Cita

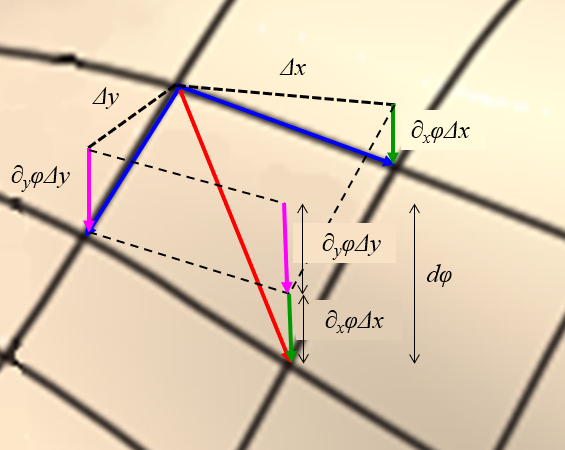
Con las pendientes se puede estimar en cuanto varia el potencial eléctrico d\varphi cunado uno se desplaza en dx y dy. Para ello basta sumar las contribuciones de cada variación

d\varphi = \partial_x\varphi dx + \partial_y\varphi dy = \displaystyle\frac{\partial\varphi}{\partial x}dx+\displaystyle\frac{\partial\varphi}{\partial y}dy

lo que se representa en el siguiente diagrama:

ID:(11606, 0)


Vector de pendiente: el gradiente
Ejercicio

Por otro lado se puede tomar cada variación como una componente de un vector lo que corresponde al gradiente


abla \varphi = \partial_x\varphi \hat{x} + \partial_y\varphi \hat{y} = \displaystyle\frac{\partial\varphi}{\partial x}\hat{x}+\displaystyle\frac{\partial\varphi}{\partial y}\hat{y}

lo que se representa en el siguiente diagrama:

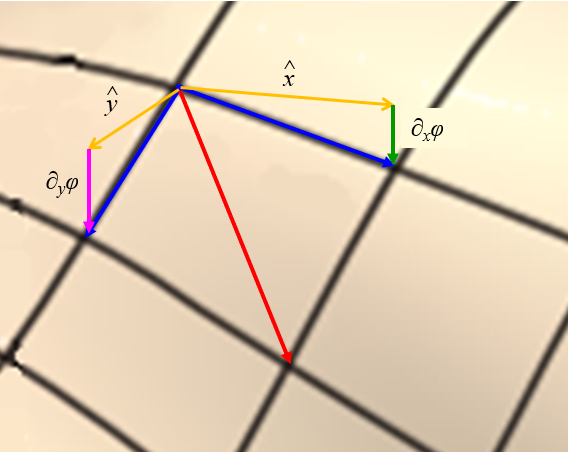
Esto no indica el cambio total si no que cuanto varia según la dirección y corresponde a la dirección en que se movería una carga si parte del punto (x,y) sin velocidad.

ID:(11607, 0)


Gradiente del potencial
Descripción

Un gradiente es un vector que se construye para una función que indica la dirección e inclinación que presenta la función en todo punto. En particular el gradiente del potencial eléctrico es igual a menos el campo eléctrico.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$\vec{E}$
&E
Campo eléctrico
V/m
$\partial/\partial x$
D_x
Derivada parcial en $x$
1/m
$\partial/\partial y$
D_y
Derivada parcial en $y$
1/m
$\partial/\partial z$
D_z
Derivada parcial en $z$
1/m
$d\varphi$
dphi
Diferencia de potencial
V
$\vec{r}$
&r
Posición
m
$V$
V
Potencial eléctrico
V
$\varphi$
phi
Potencial eléctrico
V
$dx$
dx
Variación infinitesimal en $x$
m
$dy$
dy
Variación infinitesimal en $y$
m
$dz$
dz
Variación infinitesimal en $z$
m
$\hat{x}$
&nx
Versor en $x$ (versor)
-
$\hat{y}$
&ny
Versor en $y$ (versor)
-
$\hat{z}$
&nz
Versor en $z$ (versor)
-

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Como la variación infinitesimal del potencial ($d\varphi$) resulta del producto de el campo eléctrico ($\vec{E}$) con el elemento de camino recorrido ($d\vec{s}$)

$ d\varphi = -\vec{E} \cdot d\vec{s} $



y considerando las componentes de el campo eléctrico ($\vec{E}$)

$\vec{E} = \hat{x} E_x + \hat{y} E_y + \hat{z} E_z$



junto con las de el elemento de camino recorrido ($d\vec{s}$)

$d\vec{s} = \hat{x} dx + \hat{y} dy + \hat{z} dz$



la expresi n se simplifica a

$d\varphi = -E_x dx - E_y dy - E_z dz$



Con la variaci n del potencial

$ d\varphi = \displaystyle\frac{\partial \varphi}{\partial x} dx + \displaystyle\frac{\partial \varphi}{\partial y} dy + \displaystyle\frac{\partial \varphi}{\partial z} dz $



y el gradiente calculado como

$ \nabla \varphi = \hat{x}\displaystyle\frac{\partial \varphi}{\partial x} + \hat{y}\displaystyle\frac{\partial \varphi}{\partial y} + \hat{z}\displaystyle\frac{\partial \varphi}{\partial z}$



se deduce que el gradiente del potencial es igual al negativo del campo el ctrico.

$ \vec{E} = -\nabla\varphi $

(ID 11557)

Ejemplos

El gradiente es un vector calculado para una funci n que apunta a un m ximo/m nimo pr ximo al punto en que se esta considerando.

(ID 11555)

El gradiente es un vector calculado para una funci n que apunta a un m ximo/m nimo pr ximo al punto en que se esta considerando. En el caso de una dimensi n esto coincide con la pendiente de la curva:

(ID 11558)

Si consideramos un punto (x,y) y observamos nuestro entrono podremos ver que la funci n del potencial \varphi varia tanto en la direcci n \hat{x} como \hat{y}. Si nos desplazamos una distancia \Delta x en la direcci n \hat{x}, veremos que su valor cambia de a\varphi(x,y) a \varphi(x+\Delta x,y). De igual forma lo har en la direcci n \hat{y} de un valor \varphi(x,y) a \varphi(x,y+\Delta y). En cada direcci n existir una pendiente

\partial_x\varphi =\displaystyle\frac{\varphi(x+\Delta x,y)-\varphi(x,y)}{\Delta x}

y

\partial_y\varphi =\displaystyle\frac{\varphi(x,y+\Delta y)-\varphi(x,y)}{\Delta y}

lo que se muestra en el diagrama:

Importante es hacer notar que estudiamos las pendientes en forma independiente. O sea vimos como variaban en x sin considerar cambios en y y viceversa. Las pendientes asi calculadas tambi n corresponden a derivadas pero con la restricci n de mantener todas las variables restantes fijas se denominan derivadas parciales. La noimenclatura que se usa es

\partial_x\varphi =\displaystyle\frac{\partial\varphi}{\partial x}

\partial_y\varphi =\displaystyle\frac{\partial\varphi}{\partial y}

Por ello cada vez que veamos una delta del tipo \partial pensemos en una diferencia que no considera variaciones en otras variables. En funci n de no complicarse con calculo vamos a asumir simplemente que son pendientes calculadas en forma independiente de las dem s direcciones y explorar el sentido f sico y no matem tico.

(ID 11605)

Con las pendientes se puede estimar en cuanto varia el potencial el ctrico d\varphi cunado uno se desplaza en dx y dy. Para ello basta sumar las contribuciones de cada variaci n

d\varphi = \partial_x\varphi dx + \partial_y\varphi dy = \displaystyle\frac{\partial\varphi}{\partial x}dx+\displaystyle\frac{\partial\varphi}{\partial y}dy

lo que se representa en el siguiente diagrama:

(ID 11606)

La variaci n total se puede estimar como la suma de las distintas variaciones.

$ d\varphi = \displaystyle\frac{\partial \varphi}{\partial x} dx + \displaystyle\frac{\partial \varphi}{\partial y} dy + \displaystyle\frac{\partial \varphi}{\partial z} dz $

(ID 11556)

Por otro lado se puede tomar cada variaci n como una componente de un vector lo que corresponde al gradiente


abla \varphi = \partial_x\varphi \hat{x} + \partial_y\varphi \hat{y} = \displaystyle\frac{\partial\varphi}{\partial x}\hat{x}+\displaystyle\frac{\partial\varphi}{\partial y}\hat{y}

lo que se representa en el siguiente diagrama:

Esto no indica el cambio total si no que cuanto varia seg n la direcci n y corresponde a la direcci n en que se mover a una carga si parte del punto (x,y) sin velocidad.

(ID 11607)

Podemos construir un vector tangente al campo considerando en la variaci n

$ d\varphi = \displaystyle\frac{\partial \varphi}{\partial x} dx + \displaystyle\frac{\partial \varphi}{\partial y} dy + \displaystyle\frac{\partial \varphi}{\partial z} dz $



cada componente por si sola asign ndole el versor correspondiente:

$ \nabla \varphi = \hat{x}\displaystyle\frac{\partial \varphi}{\partial x} + \hat{y}\displaystyle\frac{\partial \varphi}{\partial y} + \hat{z}\displaystyle\frac{\partial \varphi}{\partial z}$

(ID 11559)

El campo eléctrico ($\vec{E}$) es igual a menos del gradiente de el potencial eléctrico ($\varphi$):

$ \vec{E} = -\nabla\varphi $

(ID 11557)

ID:(1568, 0)