Benützer:
Gradient de Potentials
Storyboard 
Ein Gradient ist ein Vektor, der für eine Funktion erstellt wird, die die Richtung und Neigung angibt, die die Funktion an allen Punkten aufweist. Insbesondere ist der Gradient des elektrischen Potentials gleich minus dem elektrischen Feld.
ID:(1568, 0)
Gradient einer Funktion
Definition
Der Gradient ist ein Vektor, der für eine Funktion berechnet wird, die auf ein Maximum / Minimum nahe dem Punkt zeigt, an dem er betrachtet wird.
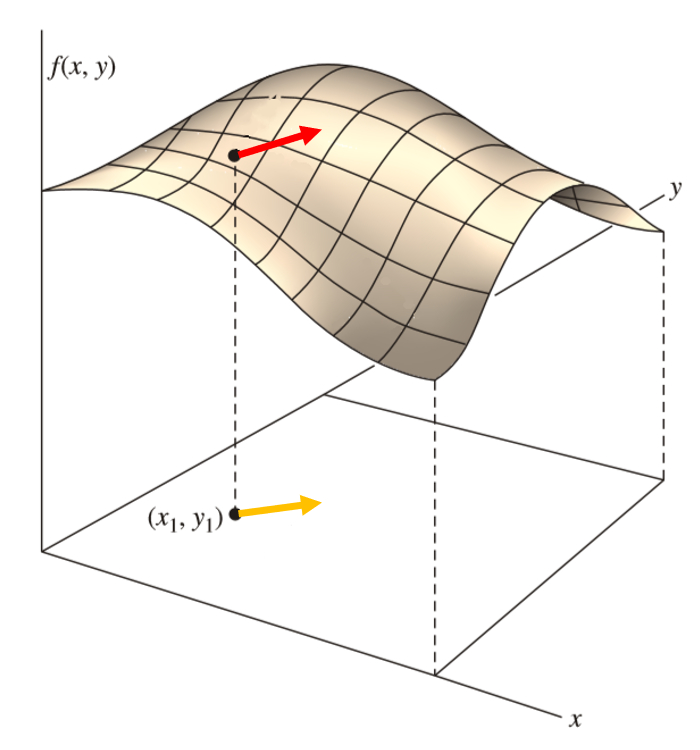
ID:(11555, 0)
Farbverlauf in einer Dimension
Bild
Der Gradient ist ein Vektor, der für eine Funktion berechnet wird, die auf ein Maximum / Minimum nahe dem Punkt zeigt, an dem er betrachtet wird. Bei einer Bemaßung stimmt dies mit der Steigung der Kurve überein:
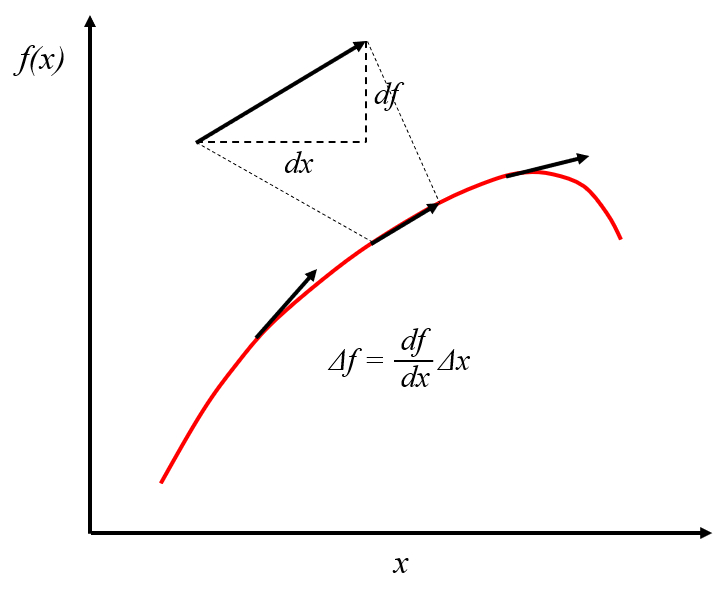
ID:(11558, 0)
Gradient in zwei Dimensionen
Notiz
Der Gradient ist ein Vektor, der für eine Funktion berechnet wird, die auf ein Maximum / Minimum nahe dem Punkt zeigt, an dem er betrachtet wird.
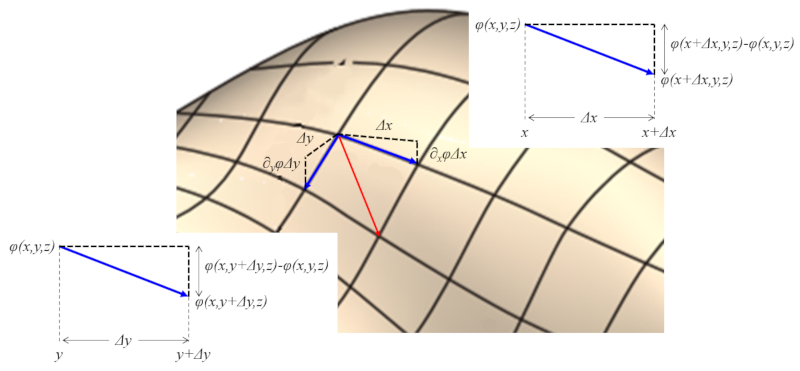
ID:(11605, 0)
Gesamtvariation
Zitat
Der Gradient ist ein Vektor, der für eine Funktion berechnet wird, die auf ein Maximum / Minimum nahe dem Punkt zeigt, an dem er betrachtet wird.
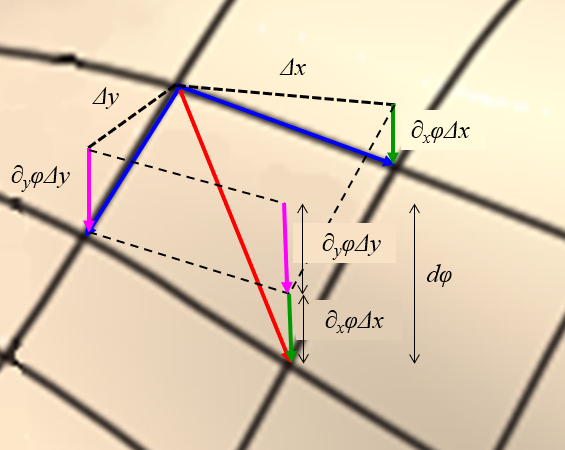
ID:(11606, 0)
Neigungsvektor: der Gradient
Übung
Der Gradient ist ein Vektor, der für eine Funktion berechnet wird, die auf ein Maximum / Minimum nahe dem Punkt zeigt, an dem er betrachtet wird.
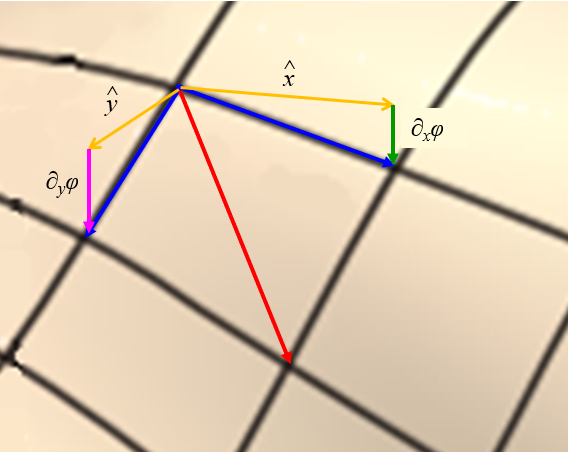
ID:(11607, 0)
Gradient de Potentials
Beschreibung
Ein Gradient ist ein Vektor, der für eine Funktion erstellt wird, die die Richtung und Neigung angibt, die die Funktion an allen Punkten aufweist. Insbesondere ist der Gradient des elektrischen Potentials gleich minus dem elektrischen Feld.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Da die Infinitesimale Variation des Potenzials ($d\varphi$) das Produkt von der Elektrisches Feld ($\vec{E}$) und der Wegelement zurückgelegt ($d\vec{s}$) ist
| $ d\varphi = -\vec{E} \cdot d\vec{s} $ |
und unter Ber cksichtigung der Komponenten von der Elektrisches Feld ($\vec{E}$)
$\vec{E} = \hat{x} E_x + \hat{y} E_y + \hat{z} E_z$
zusammen mit denen von der Wegelement zurückgelegt ($d\vec{s}$)
$d\vec{s} = \hat{x} dx + \hat{y} dy + \hat{z} dz$
kann der Ausdruck vereinfacht werden zu
$d\varphi = -E_x dx - E_y dy - E_z dz$
Mit der Ver nderung des Potentials
| $ d\varphi = \displaystyle\frac{\partial \varphi}{\partial x} dx + \displaystyle\frac{\partial \varphi}{\partial y} dy + \displaystyle\frac{\partial \varphi}{\partial z} dz $ |
und dem berechneten Gradienten
| $ \nabla \varphi = \hat{x}\displaystyle\frac{\partial \varphi}{\partial x} + \hat{y}\displaystyle\frac{\partial \varphi}{\partial y} + \hat{z}\displaystyle\frac{\partial \varphi}{\partial z}$ |
folgt, dass der Gradient des Potentials gleich dem negativen elektrischen Feld ist.
| $ \vec{E} = -\nabla\varphi $ |
(ID 11557)
Beispiele
Der Gradient ist ein Vektor, der f r eine Funktion berechnet wird, die auf ein Maximum / Minimum nahe dem Punkt zeigt, an dem er betrachtet wird.
(ID 11555)
Der Gradient ist ein Vektor, der f r eine Funktion berechnet wird, die auf ein Maximum / Minimum nahe dem Punkt zeigt, an dem er betrachtet wird. Bei einer Bema ung stimmt dies mit der Steigung der Kurve berein:
(ID 11558)
Der Gradient ist ein Vektor, der f r eine Funktion berechnet wird, die auf ein Maximum / Minimum nahe dem Punkt zeigt, an dem er betrachtet wird.
(ID 11605)
Der Gradient ist ein Vektor, der f r eine Funktion berechnet wird, die auf ein Maximum / Minimum nahe dem Punkt zeigt, an dem er betrachtet wird.
(ID 11606)
La variaci n total se puede estimar como la suma de las distintas variaciones.
| $ d\varphi = \displaystyle\frac{\partial \varphi}{\partial x} dx + \displaystyle\frac{\partial \varphi}{\partial y} dy + \displaystyle\frac{\partial \varphi}{\partial z} dz $ |
(ID 11556)
Der Gradient ist ein Vektor, der f r eine Funktion berechnet wird, die auf ein Maximum / Minimum nahe dem Punkt zeigt, an dem er betrachtet wird.
(ID 11607)
Wir k nnen einen Vektor tangieren, der das Feld unter Ber cksichtigung der Variation tangiert
| $ d\varphi = \displaystyle\frac{\partial \varphi}{\partial x} dx + \displaystyle\frac{\partial \varphi}{\partial y} dy + \displaystyle\frac{\partial \varphi}{\partial z} dz $ |
Jede Komponente weist f r sich den entsprechenden Versor zu:
| $ \nabla \varphi = \hat{x}\displaystyle\frac{\partial \varphi}{\partial x} + \hat{y}\displaystyle\frac{\partial \varphi}{\partial y} + \hat{z}\displaystyle\frac{\partial \varphi}{\partial z}$ |
(ID 11559)
Der Elektrisches Feld ($\vec{E}$) ist gleich kleiner als der Gradient von der Elektrisches Potential ($\varphi$):
| $ \vec{E} = -\nabla\varphi $ |
(ID 11557)
ID:(1568, 0)