Ejemplos de potenciales eléctricos
Storyboard 
Con los ejemplos de los campos eléctricos calculados anteriormente se calculan los potenciales eléctricos.
ID:(1562, 0)
Ejemplos de potenciales eléctricos
Descripción 
Con los ejemplos de los campos eléctricos calculados anteriormente se calculan los potenciales eléctricos.
Variables
Cálculos
Cálculos
Ecuaciones
El potencial eléctrico, carga puntual ($\varphi_p$) se calcula a partir de la integraci n radial de el campo eléctrico de una carga puntual ($E_p$) desde el radio ($r$) hasta el infinito, lo que resulta en
| $ \varphi_p = -\displaystyle\int_r^{\infty} du\,E_p$ |
Por otro lado, para la carga ($Q$), la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$), el valor de el campo eléctrico de una carga puntual ($E_p$) es
| $ E_p =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}$ |
Esto implica que al integrar
$\varphi_p = -\displaystyle\int_{r}^{\infty} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
se obtiene
| $ \varphi_p = -\displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r } $ |
(ID 11576)
Como la diferencia de potencial es el potencial eléctrico, esfera aislante, interior ($\varphi_i$) con el campo eléctrico, esfera, interior ($E_i$) y el radio ($r$), obtenemos:
| $ \varphi_i = -\displaystyle\int_0^ r du\, E_i $ |
Dado que el campo eléctrico, esfera, interior ($E_i$) con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$), el radio de la esfera ($R$) y la distancia entre cargas ($r$) es igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r }{ R ^3 }$ |
en coordenadas esf ricas tenemos:
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
Por lo tanto, el potencial eléctrico, esfera aislante, interior ($\varphi_i$) con la distancia entre cargas ($r$) resulta en:
| $ \varphi_i = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$ |
(ID 11583)
Como la diferencia de potencial es el potencial eléctrico, esfera, exterior ($\varphi_e$) con el campo eléctrico, esfera, exterior ($E_e$), el campo eléctrico, esfera, interior ($E_i$), el radio de la esfera ($R$) y el radio ($r$), obtenemos:
| $ \varphi_e = - \displaystyle\int_0^ R du\, E_i - \displaystyle\int_ R ^ r du\, E_e $ |
Dado que el campo eléctrico, esfera, exterior ($E_e$) con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la distancia entre cargas ($r$) es igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$ |
y que el campo eléctrico, esfera, interior ($E_i$) con el radio interno ($r_i$) es igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r }{ R ^3 }$ |
en coordenadas esf ricas tenemos:
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
Por lo tanto, el potencial eléctrico, esfera, exterior ($\varphi_e$) resulta en:
| $ \varphi_e = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r } $ |
(ID 11584)
El potencial eléctrico, cilindro conductor infinito ($\varphi_c$) se obtiene a trav s de la integraci n radial de el campo eléctrico, cilindro conductor infinito ($E_c$), desde el radio del cilindro ($r_0$) hasta la distancia al eje ($r$), resultando en la siguiente ecuaci n:
| $ \varphi_c = -\displaystyle\int_{r_0}^r du E_c$ |
Adem s, para las variables la carga ($Q$), la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$), el valor de el campo eléctrico, cilindro conductor infinito ($E_c$) se expresa como:
| $ E_c =\displaystyle\frac{1}{2 \pi \epsilon_0 \epsilon }\displaystyle\frac{ \lambda }{ r }$ |
Esto implica que al realizar la integraci n
$\varphi_c = -\displaystyle\int_{r_0}^r du \displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon u }= -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon } \ln\left(\displaystyle\frac{ r }{ r_0 }\right)$
se obtiene la siguiente ecuaci n:
| $ \varphi_c = -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)$ |
(ID 11585)
En el caso de una placa infinita, la relaci n entre el potencial eléctrico, placa infinita ($\varphi_s$), el campo eléctrico de una placa infinita ($E_s$) y la posición en el eje z ($z$) se establece mediante la siguiente ecuaci n:
| $ \varphi_s = -\displaystyle\int_0^z du\,E_s$ |
Asimismo, la relaci n que involucra a el campo eléctrico de una placa infinita ($E_s$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la densidad de carga por área ($\sigma$) se define como:
| $ E_s =\displaystyle\frac{ \sigma }{ 2 \epsilon_0 \epsilon }$ |
En coordenadas esf ricas, esta se expresa como:
$\varphi_s = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z$
Finalmente, la relaci n que incluye a el potencial eléctrico, placa infinita ($\varphi_s$) y la posición en el eje z ($z$) se determina por la siguiente ecuaci n:
| $ \varphi_s = -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z $ |
(ID 11586)
El potencial eléctrico, dos placas infinitas ($\varphi_d$) en relaci n con el campo eléctrico, dos placas infinitas ($E_d$) y la posición en el eje z ($z$) se expresa como:
| $ \varphi_d = -\displaystyle\int_0^z du\,E_d$ |
De manera similar, el campo eléctrico, dos placas infinitas ($E_d$) en relaci n con la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la densidad de carga por área ($\sigma$) se define como:
| $ E_d =\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }$ |
Integrando desde el origen, obtenemos:
$\varphi_d = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z$
Por lo tanto, el potencial eléctrico, dos placas infinitas ($\varphi_d$) resulta en:
| $ \varphi_d = -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z $ |
(ID 11587)
Ejemplos
En una esfera conductor con cargas, estas se distribuyen en la superficie y con ello el campo en su interior es nulo. En el exterior se comporta como una carga puntual que esta en el centro de la esfera:
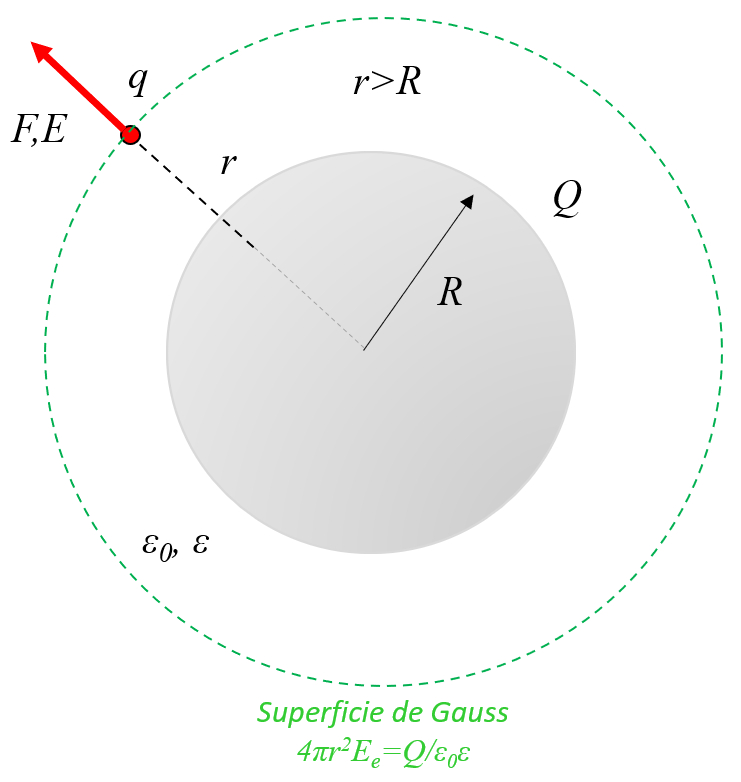
(ID 11451)
Una esfera aislante en que se ha distribuido homog neamente cargas, que no se pueden mover por ser un material aislante, tiene un campo el ctrico que crece linealmente en el interior y decrece con el inverso del radio al cuadrado:
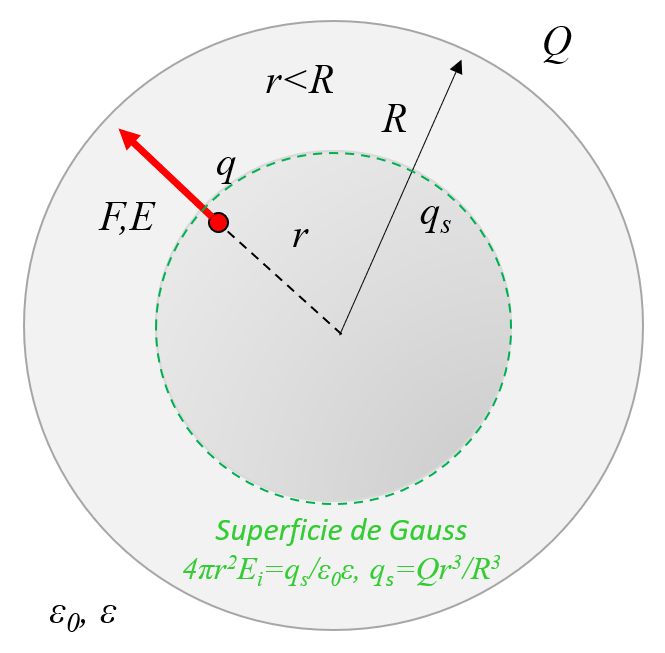
(ID 11450)
En una alambre o cilindro conductor con cargas, estas se distribuyen a lo largo del objeto comport ndose como una larga cadena de cargas puntuales alineadas en el eje:
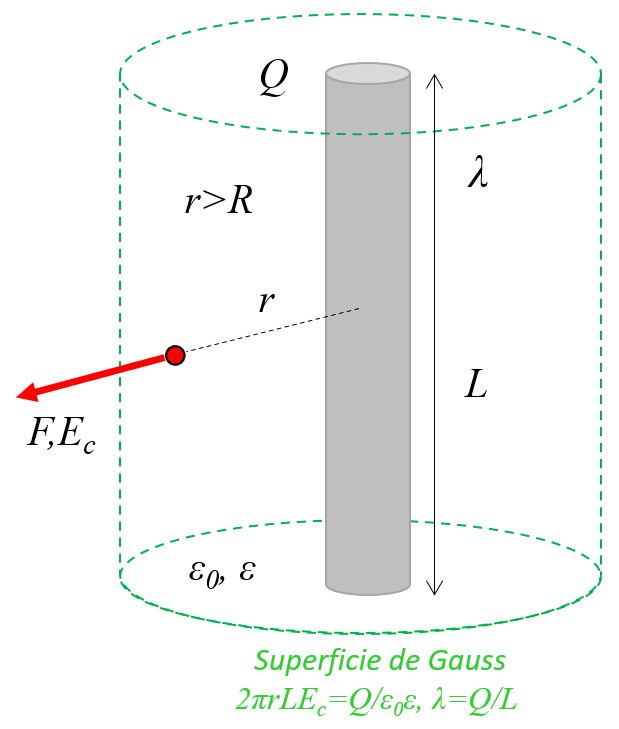
(ID 11452)
En un plano conductor, es posible definir una superficie gaussiana en forma de cilindro. Dado que las paredes laterales son ortogonales al campo el ctrico, no contribuyen al flujo neto. Por lo tanto, las nicas partes que contribuyen son las tapas del cilindro, que son superficies paralelas al plano:
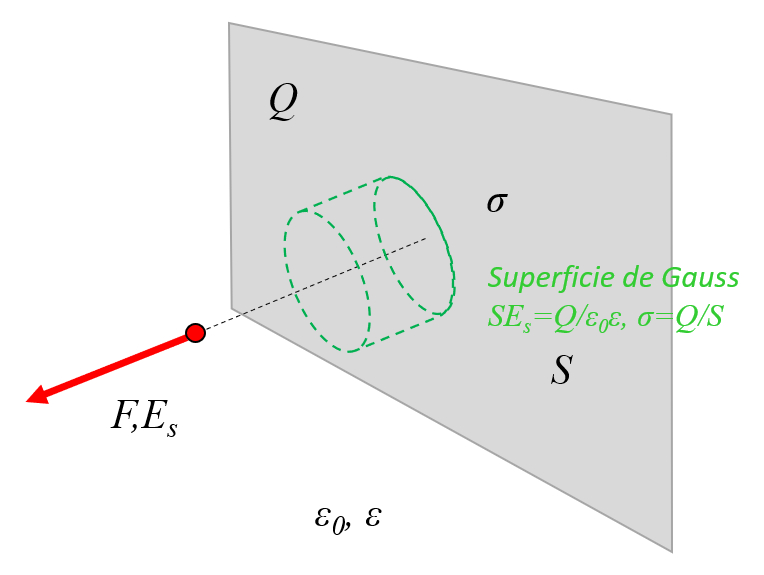
(ID 11453)
Para poder calcular en forma simple el campo entre las dos placas se puede asumir que el campo externo se compensa y que la mayor parte es solo entre las placas:
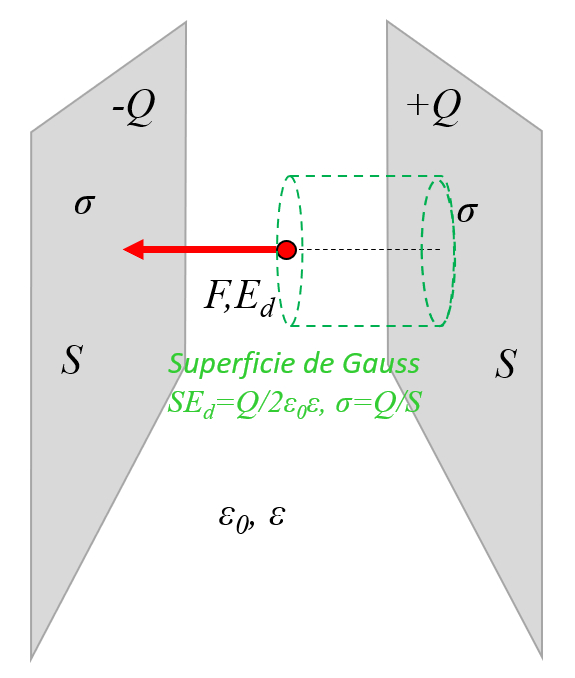
(ID 11455)
ID:(1562, 0)
