Beispiele für elektrische Potentiale
Storyboard 
Mit den vorher berechneten Beispielen der elektrischen Felder werden die elektrischen Potentiale berechnet.
ID:(1562, 0)
Leiterkugel mit Ladung
Definition 
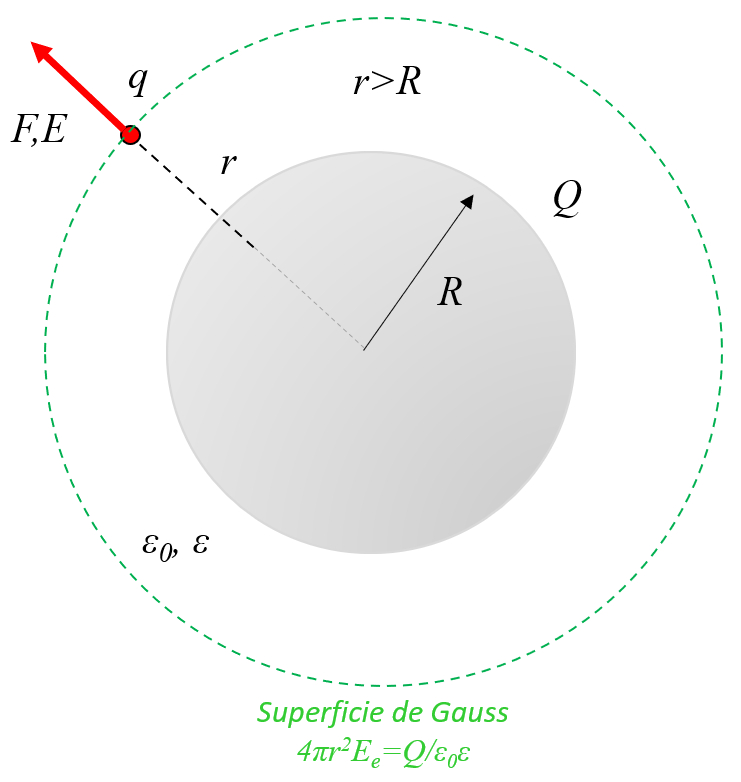
In einer leitenden Kugel mit Ladungen sind diese auf der Oberfläche verteilt und damit ist das Feld im Inneren null. Draußen verhält es sich wie eine Punktladung, die sich in der Mitte der Kugel befindet:
ID:(11451, 0)
Isolierkugel mit homogener Ladung
Bild 
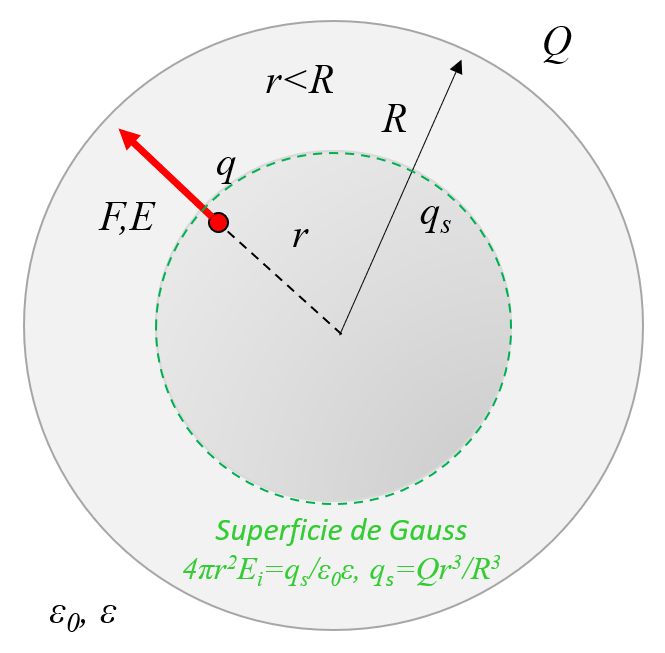
Eine isolierende Kugel, in der Ladungen homogen verteilt wurden und die nicht bewegt werden kann, weil es sich um ein isolierendes Material handelt, hat ein elektrisches Feld, das im Inneren linear wächst und mit der Umkehrung des quadratischen Radius abnimmt:
ID:(11450, 0)
Geladener unendlicher Draht oder Zylinder im Vakuum
Notiz 
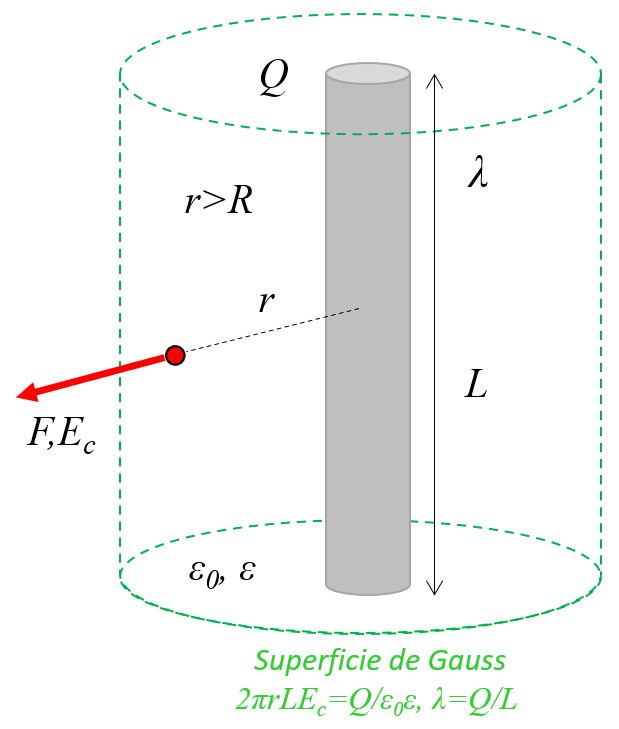
In einem Leiterdraht oder Zylinder mit Ladungen sind diese über das Objekt verteilt und verhalten sich wie eine lange Kette von Punktlasten, die auf der Achse ausgerichtet sind:
ID:(11452, 0)
Unendliche Leiterebene mit Last
Zitat 
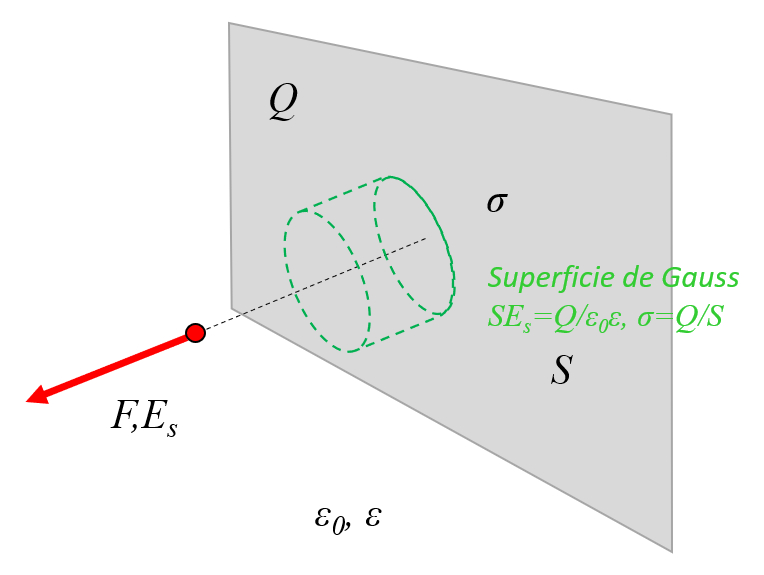
In einer leitenden Ebene kann eine Gaußsche Fläche als Zylinder definiert werden. Da die Seitenwände orthogonal zum elektrischen Feld stehen, tragen sie nicht zum Nettofluss bei. Daher sind die einzigen Teile, die beitragen, die Endkappen des Zylinders, die Flächen parallel zur Ebene sind:
ID:(11453, 0)
Einfaches Modell für zwei Platten mit entgegengesetzten Ladungen
Übung 
Um das Feld zwischen den beiden Platten auf einfache Weise berechnen zu können, kann davon ausgegangen werden, dass das externe Feld kompensiert wird und dass sich das meiste nur zwischen den Platten befindet:
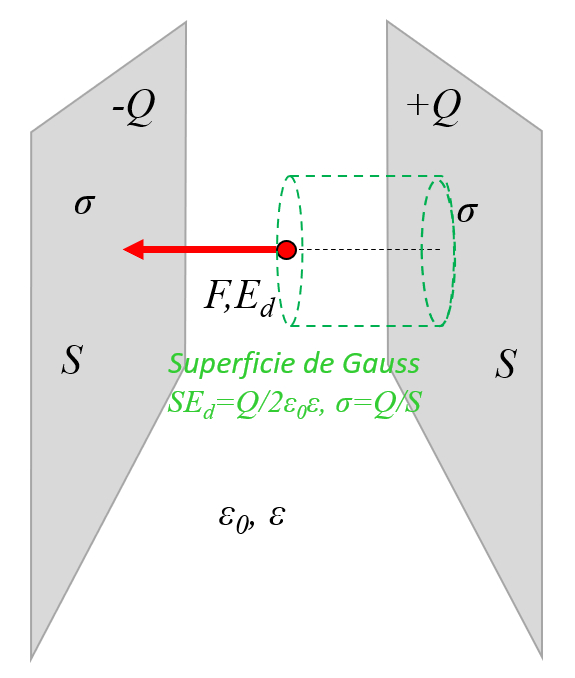
ID:(11455, 0)
Beispiele für elektrische Potentiale
Beschreibung 
Mit den vorher berechneten Beispielen der elektrischen Felder werden die elektrischen Potentiale berechnet.
Variablen
Berechnungen
Berechnungen
Gleichungen
Der Elektrisches Potential, Punktladung ($\varphi_p$) wird durch die radiale Integration von das Elektrisches Feld einer Punktladung ($E_p$) von der Radius ($r$) bis unendlich berechnet, was ergibt
| $ \varphi_p = -\displaystyle\int_r^{\infty} du\,E_p$ |
Andererseits ist f r die Ladung ($Q$), die Dielektrizitätskonstante ($\epsilon$) und die Elektrische Feldkonstante ($\epsilon_0$) der Wert von das Elektrisches Feld einer Punktladung ($E_p$)
| $ E_p =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}$ |
Das bedeutet, dass durch die Integration
$\varphi_p = -\displaystyle\int_{r}^{\infty} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
wir erhalten
| $ \varphi_p = -\displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r } $ |
(ID 11576)
Da der Potentialunterschied der Elektrisches Potential, isolierende Kugel, innen ($\varphi_i$) mit der Elektrisches Feld, Kugel, Innenraum ($E_i$) und der Radius ($r$) ist, ergibt sich:
| $ \varphi_i = -\displaystyle\int_0^ r du\, E_i $ |
Da der Elektrisches Feld, Kugel, Innenraum ($E_i$) mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$), der Kugelradius ($R$) und die Entfernung zwischen Ladungen ($r$) gleich ist:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r }{ R ^3 }$ |
In sph rischen Koordinaten haben wir:
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
Daher ergibt sich der Elektrisches Potential, isolierende Kugel, innen ($\varphi_i$) mit die Entfernung zwischen Ladungen ($r$) in:
| $ \varphi_i = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$ |
(ID 11583)
Da der Potentialunterschied der Elektrisches Potential, Kugel, außen ($\varphi_e$) mit der Elektrisches Feld, Kugel, außen ($E_e$), der Elektrisches Feld, Kugel, Innenraum ($E_i$), der Kugelradius ($R$) und der Radius ($r$) ist, ergibt sich:
| $ \varphi_e = - \displaystyle\int_0^ R du\, E_i - \displaystyle\int_ R ^ r du\, E_e $ |
Da der Elektrisches Feld, Kugel, außen ($E_e$) mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Entfernung zwischen Ladungen ($r$) gleich ist:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$ |
und der Elektrisches Feld, Kugel, Innenraum ($E_i$) mit der Inneres Radius ($r_i$) gleich ist:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r }{ R ^3 }$ |
In sph rischen Koordinaten haben wir:
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
Daher ergibt sich der Elektrisches Potential, Kugel, außen ($\varphi_e$) in:
| $ \varphi_e = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r } $ |
(ID 11584)
Der Elektrisches Potential, unendlich leitender Zylinder ($\varphi_c$) wird durch die radiale Integration von der Elektrisches Feld, unendlich leitender Zylinder ($E_c$) von der Zylinderradius ($r_0$) bis die Achsabstand ($r$) berechnet, was zu folgender Gleichung f hrt:
| $ \varphi_c = -\displaystyle\int_{r_0}^r du E_c$ |
Des Weiteren ist der Wert von der Elektrisches Feld, unendlich leitender Zylinder ($E_c$) f r die Variablen die Ladung ($Q$), die Dielektrizitätskonstante ($\epsilon$) und die Elektrische Feldkonstante ($\epsilon_0$) durch die folgende Gleichung gegeben:
| $ E_c =\displaystyle\frac{1}{2 \pi \epsilon_0 \epsilon }\displaystyle\frac{ \lambda }{ r }$ |
Dies impliziert, dass durch die Durchf hrung der Integration
$\varphi_c = -\displaystyle\int_{r_0}^r du \displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon u }= -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon } \ln\left(\displaystyle\frac{ r }{ r_0 }\right)$
die folgende Gleichung erhalten wird:
| $ \varphi_c = -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)$ |
(ID 11585)
Im Fall einer unendlichen Platte wird die Beziehung zwischen der Elektrisches Potential, unendliche Platte ($\varphi_s$), der Elektrisches Feld einer unendlichen Platte ($E_s$) und die Position auf der z-Achse ($z$) durch die folgende Gleichung festgelegt:
| $ \varphi_s = -\displaystyle\int_0^z du\,E_s$ |
Ebenso wird die Beziehung, die der Elektrisches Feld einer unendlichen Platte ($E_s$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Ladungsdichte nach Fläche ($\sigma$) einbezieht, wie folgt definiert:
| $ E_s =\displaystyle\frac{ \sigma }{ 2 \epsilon_0 \epsilon }$ |
In sph rischen Koordinaten wird dies ausgedr ckt als:
$\varphi_s = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z$
Schlie lich wird die Beziehung, die der Elektrisches Potential, unendliche Platte ($\varphi_s$) und die Position auf der z-Achse ($z$) umfasst, durch die folgende Gleichung bestimmt:
| $ \varphi_s = -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z $ |
(ID 11586)
Der Elektrisches Potential, unendliche Platten ($\varphi_d$) in Bezug auf der Elektrisches Feld, zwei unendliche Platten ($E_d$) und die Position auf der z-Achse ($z$) wird wie folgt ausgedr ckt:
| $ \varphi_d = -\displaystyle\int_0^z du\,E_d$ |
hnlich wird der Elektrisches Feld, zwei unendliche Platten ($E_d$) in Bezug auf die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Ladungsdichte nach Fläche ($\sigma$) definiert durch:
| $ E_d =\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }$ |
Durch Integration vom Ursprung erhalten wir:
$\varphi_d = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z$
Daher ergibt sich der Elektrisches Potential, unendliche Platten ($\varphi_d$) durch:
| $ \varphi_d = -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z $ |
(ID 11587)
Beispiele
Elektrische Potentiale, die die potenzielle Energie pro Ladungseinheit darstellen, beeinflussen, wie sich die Geschwindigkeit eines Teilchens ndert. Daher folgt aus der Energieerhaltung zwischen zwei Punkten, dass in Anwesenheit der Variablen die Ladung ($q$), die Partikelmasse ($m$), die Geschwindigkeit 1 ($v_1$), die Geschwindigkeit 2 ($v_2$), der Elektrisches Potential 1 ($\varphi_1$) und der Elektrisches Potential 2 ($\varphi_2$) die folgende Beziehung erf llt sein muss:
| $ \displaystyle\frac{1}{2} m v_1 ^2 + q \varphi_1 = \displaystyle\frac{1}{2} m v_2 ^2 + q \varphi_2 $ |
(ID 11596)
In einer leitenden Kugel mit Ladungen sind diese auf der Oberfl che verteilt und damit ist das Feld im Inneren null. Drau en verh lt es sich wie eine Punktladung, die sich in der Mitte der Kugel befindet:

(ID 11451)
Der Elektrisches Potential, Punktladung ($\varphi_p$) ist mit die Ladung ($Q$), die Entfernung zwischen Ladungen ($r$), die Dielektrizitätskonstante ($\epsilon$) und die Elektrische Feldkonstante ($\epsilon_0$) gleich:
| $ \varphi_p = -\displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r } $ |
(ID 11576)
Como la diferencia de potencial con es igual
| $ \varphi_f = -\displaystyle\int_r^{\infty} du\,E_f(u)$ |
con
| $ E_f =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}\theta( r - R )$ |
lo que en coordenadas esf ricas es
$\varphi_f = -\displaystyle\int_{\infty}^{r} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
o sea con
| $ \varphi_f = -\displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r } $ |
(ID 11582)
Eine isolierende Kugel, in der Ladungen homogen verteilt wurden und die nicht bewegt werden kann, weil es sich um ein isolierendes Material handelt, hat ein elektrisches Feld, das im Inneren linear w chst und mit der Umkehrung des quadratischen Radius abnimmt:

(ID 11450)
Der Elektrisches Potential, isolierende Kugel, innen ($\varphi_i$) ist mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$), die Entfernung zwischen Ladungen ($r$) und der Kugelradius ($R$) ist gleich:
| $ \varphi_i = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$ |
(ID 11583)
Der Elektrisches Potential, Kugel, außen ($\varphi_e$) ist mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Entfernung zwischen Ladungen ($r$) ist gleich:
| $ \varphi_e = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r } $ |
(ID 11584)
In einem Leiterdraht oder Zylinder mit Ladungen sind diese ber das Objekt verteilt und verhalten sich wie eine lange Kette von Punktlasten, die auf der Achse ausgerichtet sind:

(ID 11452)
Der Elektrisches Potential, unendlich leitender Zylinder ($\varphi_c$) ist mit der Pi ($\pi$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$), die Lineare Ladungsdichte ($\lambda$), die Achsabstand ($r$) und der Zylinderradius ($r_0$) ist gleich:
| $ \varphi_c = -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)$ |
(ID 11585)
In einer leitenden Ebene kann eine Gau sche Fl che als Zylinder definiert werden. Da die Seitenw nde orthogonal zum elektrischen Feld stehen, tragen sie nicht zum Nettofluss bei. Daher sind die einzigen Teile, die beitragen, die Endkappen des Zylinders, die Fl chen parallel zur Ebene sind:

(ID 11453)
Der Elektrisches Potential, unendliche Platte ($\varphi_s$) ist mit die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$), die Ladungsdichte nach Fläche ($\sigma$) und die Position auf der z-Achse ($z$) ist gleich:
| $ \varphi_s = -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z $ |
(ID 11586)
Um das Feld zwischen den beiden Platten auf einfache Weise berechnen zu k nnen, kann davon ausgegangen werden, dass das externe Feld kompensiert wird und dass sich das meiste nur zwischen den Platten befindet:

(ID 11455)
Der Elektrisches Potential, unendliche Platten ($\varphi_d$) ist mit die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$), die Ladungsdichte nach Fläche ($\sigma$) und die Position auf der z-Achse ($z$) ist gleich:
| $ \varphi_d = -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z $ |
(ID 11587)
ID:(1562, 0)
