Utilizador:
Energia interna
Storyboard 
A energia interna de um sistema consiste em energia cinética e energia potencial. A energia cinética está associada ao calor e pode ser relacionada às oscilações dos átomos em torno de seus pontos de equilíbrio. Por outro lado, a energia potencial está associada ao trabalho que o sistema é capaz de realizar.
ID:(1469, 0)
Mecanismos
Iframe
A energia interna é a energia total contida em um sistema termodinâmico devido às energias cinética e potencial de suas moléculas. Ela inclui a energia proveniente do movimento molecular (translacional, rotacional e vibracional) e a energia das interações intermoleculares e das ligações químicas. A energia interna é uma função de estado, o que significa que depende apenas do estado atual do sistema e não de como o sistema alcançou esse estado. As mudanças na energia interna ocorrem quando calor é adicionado ou removido do sistema ou quando trabalho é realizado sobre ou pelo sistema. Este conceito é fundamental na termodinâmica, descrevendo as mudanças de energia em processos como processos isotérmicos, adiabáticos, isobáricos e isocóricos. A energia interna ajuda a determinar os estados de equilíbrio e a estabilidade do sistema, já que os sistemas tendem a se mover para estados com menor energia interna. Ela fornece uma medida abrangente de todas as formas microscópicas de energia dentro de um sistema, essencial para entender as transformações de energia em diversos processos.
Mecanismos
ID:(15245, 0)
Energia cinética
Conceito
Energia cinética de translação: Essa energia está associada ao movimento linear das partículas no sistema. Quanto maior a velocidade de translação das partículas, maior a sua energia cinética de translação.
Energia cinética de rotação: Algumas partículas, como átomos ou moléculas, podem girar em torno de um eixo. Essa rotação está associada à energia cinética de rotação, que depende da massa e da velocidade angular das partículas.
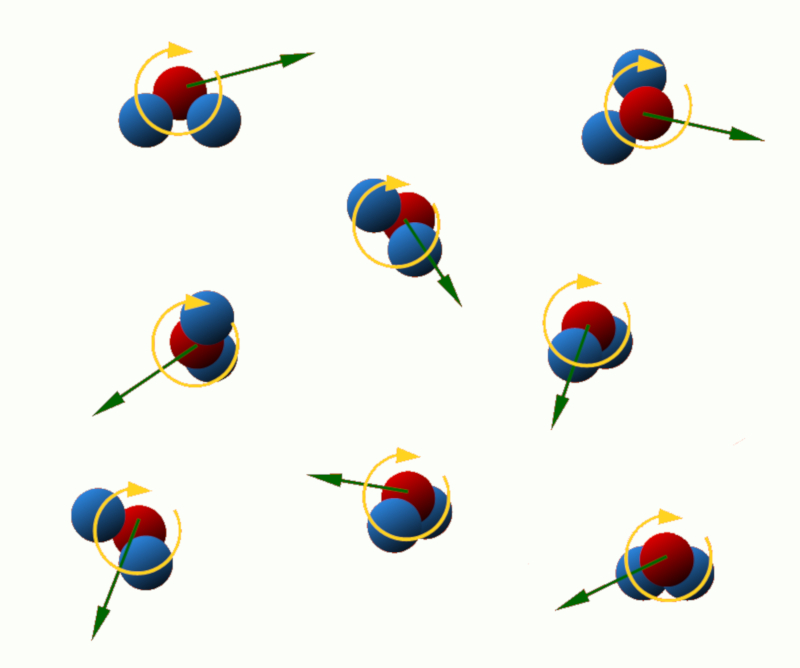
ID:(11122, 0)
Energia de ligação
Conceito
Energia potencial de ligação: Essa energia está relacionada às forças de interação entre as partículas do sistema. Por exemplo, em um sólido, a energia de ligação é devido às forças de atração entre átomos ou moléculas vizinhas.
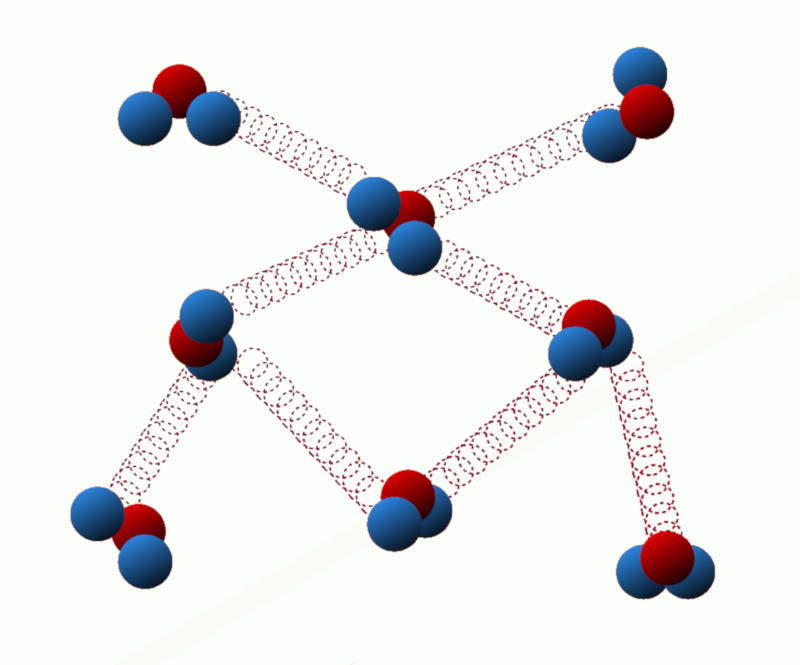
ID:(11123, 0)
Energia química
Conceito
Energia de excitação: Alguns sistemas podem sofrer mudanças em seu estado energético, como quando elétrons em um átomo ou molécula são excitados. A energia associada a esses estados excitados é conhecida como energia de excitação.
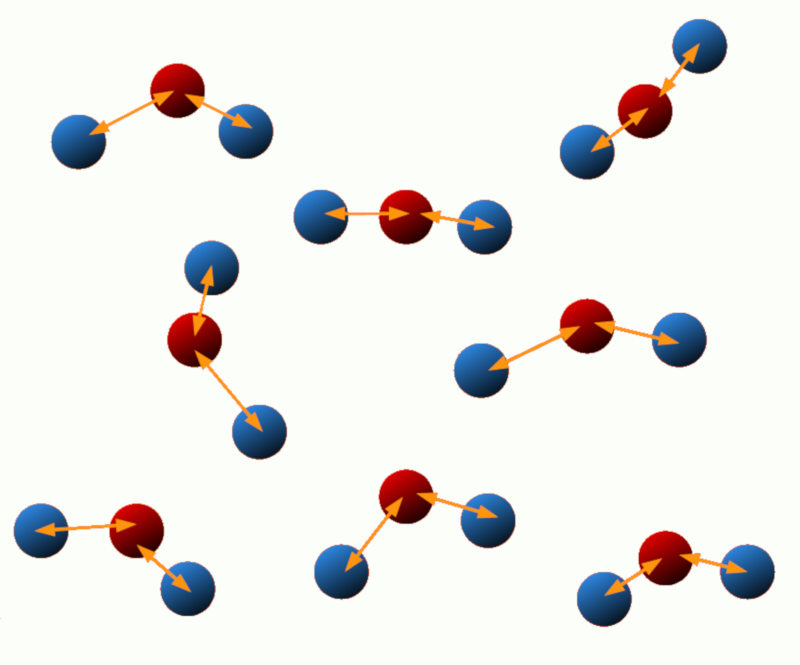
ID:(11124, 0)
Energia de excitação
Conceito
Energia química (energia elétrica): Em sistemas químicos, reações químicas podem liberar ou absorver energia. Essa energia é conhecida como energia química e está relacionada às ligações químicas presentes nas moléculas.
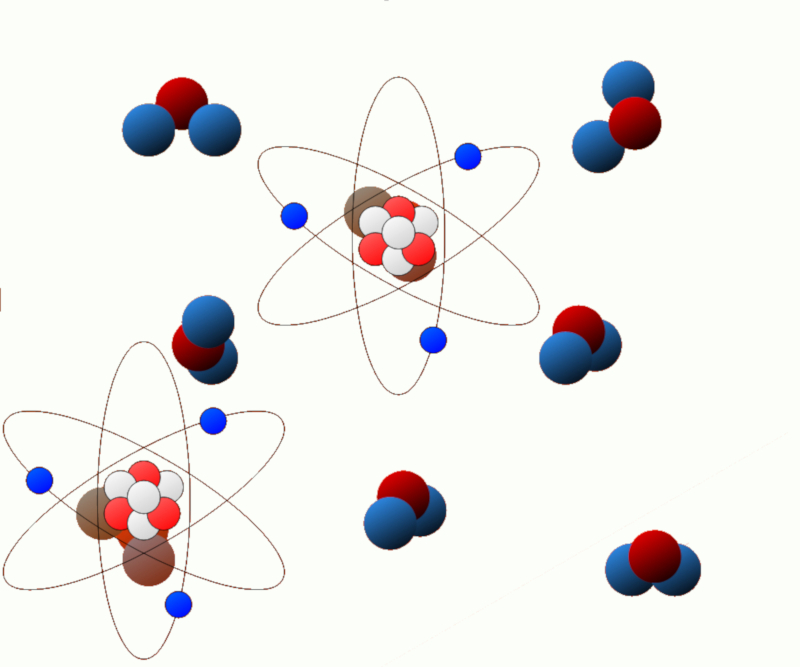
ID:(11125, 0)
Energia interna
Conceito
A energia interna é a energia total possuída pelas partículas que compõem um sistema. Essas energias incluem:
• Energia cinética de translação: Essa energia está associada ao movimento linear das partículas no sistema. Quanto maior a velocidade de translação das partículas, maior a sua energia cinética de translação.
• Energia cinética de rotação: Algumas partículas, como átomos ou moléculas, podem girar em torno de um eixo. Essa rotação está associada à energia cinética de rotação, que depende da massa e da velocidade angular das partículas.
• Energia potencial de ligação: Essa energia está relacionada às forças de interação entre as partículas do sistema. Por exemplo, em um sólido, a energia de ligação é devido às forças de atração entre átomos ou moléculas vizinhas.
• Energia química (energia elétrica): Em sistemas químicos, reações químicas podem liberar ou absorver energia. Essa energia é conhecida como energia química e está relacionada às ligações químicas presentes nas moléculas.
• Energia de excitação: Alguns sistemas podem sofrer mudanças em seu estado energético, como quando elétrons em um átomo ou molécula são excitados. A energia associada a esses estados excitados é conhecida como energia de excitação.
ID:(11121, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ E = K + V $
E = K + V
$ K = K_t + K_r $
K = K_t + K_r
$ K_r =\displaystyle\frac{1}{2} I \omega ^2$
K_r = I * omega ^2/2
$ K_t =\displaystyle\frac{1}{2} m_i v ^2$
K_t = m_i * v ^2/2
ID:(15304, 0)
Energia cinética translacional
Equação
No caso em que se estuda a translação, a definição de energia
| $ dW = \vec{F} \cdot d\vec{s} $ |
é aplicada ao segundo princípio de Newton
| $ F = m_i a $ |
resultando na expressão
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
A energia necessária para que um objeto passe da velocidade $v_1$ para a velocidade $v_2$ pode ser calculada usando a definição com
| $ dW = \vec{F} \cdot d\vec{s} $ |
Com a segunda lei de Newton, essa expressão pode ser reescrita como
$\Delta W = m a \Delta s = m\displaystyle\frac{\Delta v}{\Delta t}\Delta s$
Usando a definição de velocidade com
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
obtemos
$\Delta W = m\displaystyle\frac{\Delta v}{\Delta t}\Delta s = m v \Delta v$
onde a diferença de velocidades é
$\Delta v = v_2 - v_1$
Além disso, a velocidade em si pode ser aproximada pela velocidade média
$v = \displaystyle\frac{v_1 + v_2}{2}$
Usando ambas as expressões, obtemos a expressão
$\Delta W = m v \Delta v = m(v_2 - v_1)\displaystyle\frac{(v_1 + v_2)}{2} = \displaystyle\frac{m}{2}(v_2^2 - v_1^2)$
Portanto, a energia varia conforme
$\Delta W = \displaystyle\frac{m}{2}v_2^2 - \displaystyle\frac{m}{2}v_1^2$
Dessa forma, podemos definir a energia cinética
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
ID:(3244, 0)
Energia cinética rotacional
Equação
No caso em que se estuda a translação, a definição de energia
| $ \Delta W = T \Delta\theta $ |
é aplicada à segunda lei de Newton
| $ T = I \alpha $ |
resultando na expressão
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
A energia necessária para que um objeto passe da velocidade angular $\omega_1$ para a velocidade angular $\omega_2$ pode ser calculada usando a definição
| $ \Delta W = T \Delta\theta $ |
Com a segunda lei de Newton, podemos reescrever essa expressão como
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Usando a definição de velocidade angular
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
obtemos
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
A diferença entre as velocidades angulares é
$\Delta\omega=\omega_2-\omega_1$
Por outro lado, a própria velocidade angular pode ser aproximada pela velocidade angular média
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Usando ambas as expressões, obtemos a equação
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Assim, a energia varia de acordo com
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Podemos usar isso para definir a energia cinética
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)
Energia cinética total
Equação
A energia cinética pode ser de translação e/ou de rotação. Portanto, a energia cinética total é a soma de ambas:
| $ K = K_t + K_r $ |
ID:(3686, 0)
Energia total
Equação
A energia total corresponde à soma da energia cinética total e da energia potencial:
| $ E = K + V $ |
ID:(3687, 0)