Usuario:
Acción y Reacción
Storyboard 
El tercer principio de Newton define que las fuerzas tienen que ser generadas en pares de modo que su suma es cero. Esto implica que ante una acción siempre existe una reacción de igual magnitud pero sentido contrario.
ID:(755, 0)
Acción y Reacción
Storyboard
El tercer principio de Newton define que las fuerzas tienen que ser generadas en pares de modo que su suma es cero. Esto implica que ante una acción siempre existe una reacción de igual magnitud pero sentido contrario.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Como la variación del momento ($\Delta p$) es igual a la masa inercial ($m_i$) por la diferencia de velocidad ($\Delta v$), tenemos:
Para el caso en que la masa es constante, la variaci n del momento puede expresarse con el momento ($p$) y el momento inicial ($p_0$), lo que nos da:
Al combinarlo con la velocidad ($v$) y la velocidad inicial ($v_0$), obtenemos:
$\Delta p = p - p_0 = m_i v - m_i v_0 = m_i ( v - v_0 ) = m_i \Delta v$
Donde la diferencia de velocidad ($\Delta v$) es calculado por:
Y as , llegamos a:
Como la variación del momento ($\Delta p$) es igual a la masa inercial ($m_i$) por la diferencia de velocidad ($\Delta v$), tenemos:
Para el caso en que la masa es constante, la variaci n del momento puede expresarse con el momento ($p$) y el momento inicial ($p_0$), lo que nos da:
Al combinarlo con la velocidad ($v$) y la velocidad inicial ($v_0$), obtenemos:
$\Delta p = p - p_0 = m_i v - m_i v_0 = m_i ( v - v_0 ) = m_i \Delta v$
Donde la diferencia de velocidad ($\Delta v$) es calculado por:
Y as , llegamos a:
Ejemplos
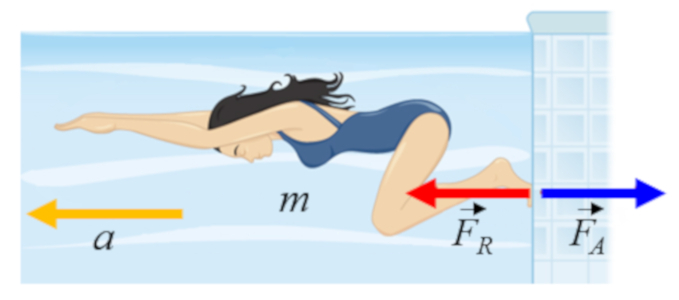
Cuando una nadadora se impulsa, ejerce una fuerza de una fuerza de acción ($F_A$) sobre la pared de la piscina, lo que a su vez genera una fuerza de una fuerza de reacción ($F_R$) sobre su cuerpo, propulsando as su desplazamiento:
Si intentamos ejercer fuerza contra una pared, notaremos que la principal limitaci n est dada por la adherencia de nuestros zapatos al suelo. Si el suelo es liso, es probable que empecemos a resbalar, lo que limitar la fuerza que podemos ejercer.
Es interesante destacar que si empujamos en una direcci n no horizontal, la componente vertical afectar nuestra fuerza vertical contra el suelo. En otras palabras, la reacci n vertical a nuestra acci n sobre la pared provocar un aumento (si estamos empujando hacia arriba) o una disminuci n (si estamos empujando hacia abajo) en nuestro peso.
Cada vez que caminamos, debemos impulsar nuestro cuerpo en cada paso. Para ello, colocamos el pie en el suelo y, suponiendo que no se deslice debido a la fricci n, nuestros m sculos ejercen una fuerza sobre nuestro cuerpo que lo impulsa y transmite la reacci n al pie, que a su vez la transmite al suelo (el planeta):
Debido a que el planeta es gigantesco, no se puede observar directamente el efecto de esta reacci n. Sin embargo, si estamos parados sobre un objeto m s peque o, como un cilindro, podemos inducir su rodaje avanzando en relaci n a nuestra posici n sobre el cilindro, mientras que el cilindro rueda en la direcci n opuesta.
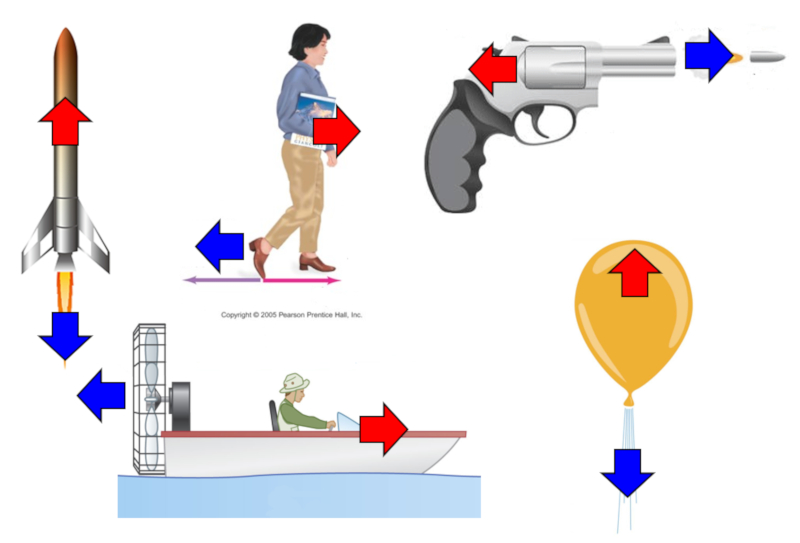
Un aspecto importante de la fuerza es que no puede ser creada de la nada. Cada vez que intentamos generar una fuerza de acción ($F_A$) (una acci n), se generar inevitablemente una fuerza de reacción ($F_R$) con la misma magnitud pero direcci n opuesta:
En otras palabras, las fuerzas siempre se crean en pares, y la suma de estos pares siempre es igual a cero.
La fuerza ($F$) se define como la variación del momento ($\Delta p$) por el tiempo transcurrido ($\Delta t$) que se define con la relaci n:
La fuerza ($F$) se define como la variación del momento ($\Delta p$) por el tiempo transcurrido ($\Delta t$) que se define con la relaci n:
Cuando la masa inercial ($m_i$) es constante, la variación del momento ($\Delta p$) es proporcional a la diferencia de velocidad ($\Delta v$):
Cuando la masa inercial ($m_i$) es constante, la variación del momento ($\Delta p$) es proporcional a la diferencia de velocidad ($\Delta v$):
ID:(755, 0)
