Storyboard

Eine wichtige Einschränkung ist die Geschwindigkeit, mit der ein System mit Energie versorgt werden kann. Dies ist besonders kritisch im Durchschnitt, wenn das System sehr schnell Energie verliert.Sie führen das Konzept der Leistung ein, das als die pro Zeiteinheit zugeführte oder verlorene Energie definiert wird.

>Modell

ID:(602, 0)

Bild

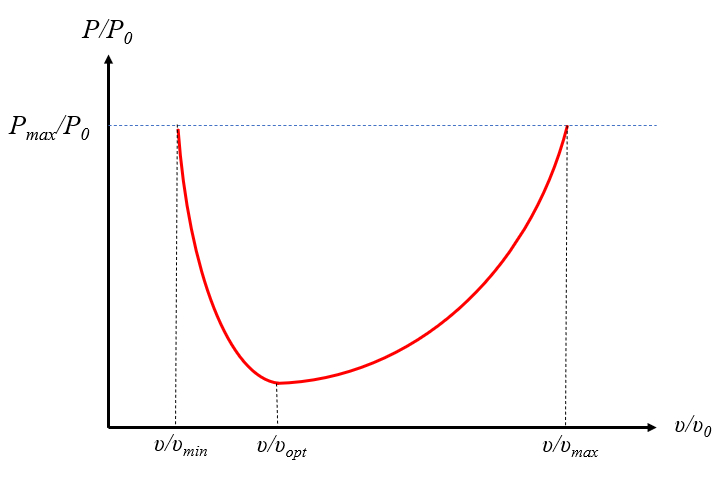
Eines der Beispiele, die verdeutlichen, wie wichtig die Leistung ist, um die Begrenzung der Bewegung zu verstehen, ist der Flug von Vögeln. Die Leistungskurve als Funktion der Fluggeschwindigkeit zeigt drei Hauptmerkmale auf:

• Sie steigt bei niedrigen Geschwindigkeiten aufgrund des Verlusts von Auftrieb und des Phänomens des sogenannten akustischen Kurzschlusses. In letzterem Fall nimmt der Auftrieb ab, weil hoher Druck von unten unter den Flügeln zur Oberseite entlang des äußeren Rands entweicht. Um diesen Effekt zu vermeiden und Treibstoff zu sparen, verfügen moderne Flugzeuge über Winglets, das sind kurze senkrechte Erweiterungen an den Flügeln. Diese Begrenzung bedeutet, dass auch Vögel eine Start- und Landestrecke benötigen; sie können nicht aus dem Stand starten oder ohne Laufen landen.

• Ein Minimumpunkt der Leistung, den Zugvögel nutzen, um lange Strecken mit geringem Energieverbrauch zurückzulegen. Dieses Minimum hängt von der Form der Flügel ab, was bedeutet, dass nur einige Vogelarten die Fähigkeit zur Migration haben.

• Ein Maximumpunkt der Leistung tritt bei hohen Geschwindigkeiten auf und führt zu einem höheren Energieverbrauch für schnellere Flüge. Auch hier ist die Form der Flügel entscheidend, um hohe Geschwindigkeiten zu erreichen, was Vögel der Beute kennzeichnet. Typischerweise sind Flügeldesigns von Vögeln entweder für die Jagd oder die Migration optimiert, wobei nur wenige Arten beide Strategien nutzen.

ID:(51, 0)