Modelo nalgas y pectorales
Definición 
Las nalgas y pectorales se modelan como mitades de elipsoides adosados a los conos truncados. Para ello se deben definir tanto las coordenadas del centro
En el caso de la cadera las posiciones en la altura coinciden con la altura de la cadera misma mientras que en los pectorales debemos alienarlos con la parte superior del tórax.
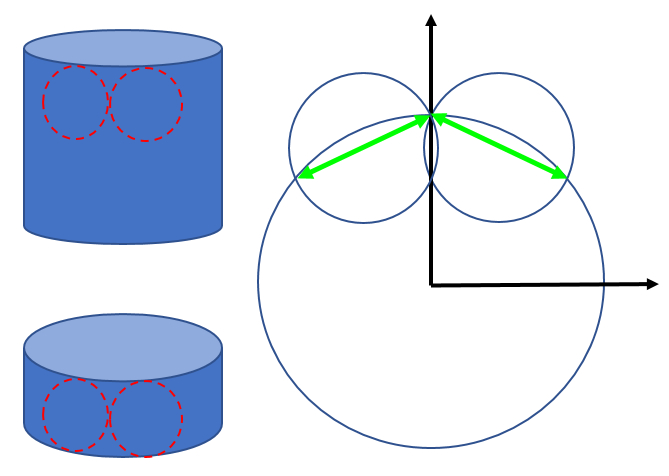
Las dimensiones se deben estimar determinando perímetros o secciones de estos.
ID:(309, 0)
Geometría de nalgas y pectorales
Imagen 
Si se superponen las mitades de los elipsoides sobre los conos truncados y se mide el perímetro la huincha de medir recorrerá algo asi como la siguiente linea roja:
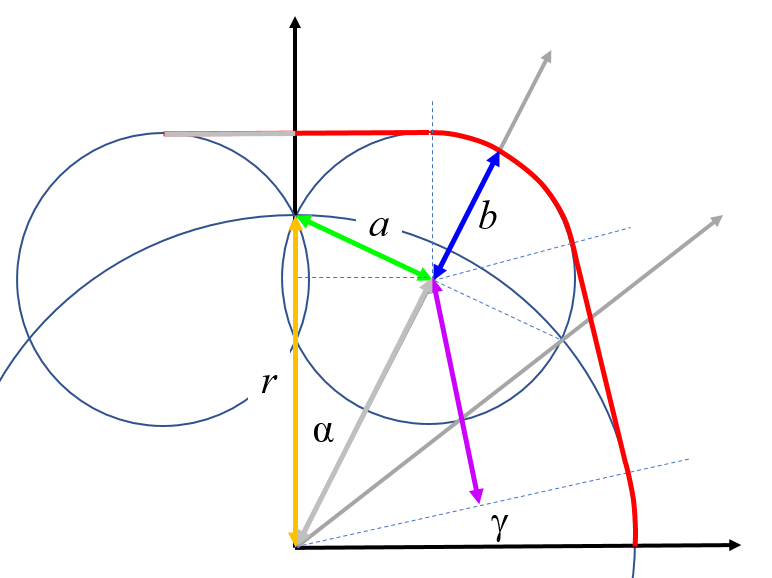
Entre nalgas/pectorales la hincha hace un puente (sección superior), luego se adhiere a la nalga/pectoral para luego continuar tangencialmente de un cuerpo al otro. El resto del recorrido (espalda) es igual al perímetro del cono truncado.
ID:(10528, 0)
Nalgas
Nota 
Las nalgas se modela mediante semielipsoides con el semieje vertical
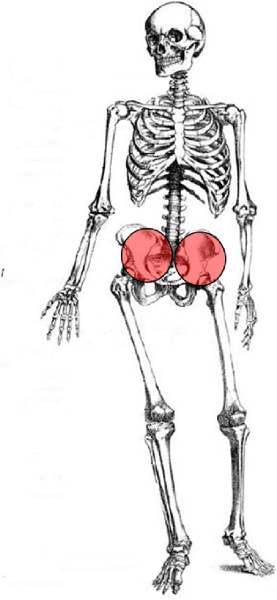
ID:(2128, 0)
Perímetro mayor sobre nalgas s_6
Cita 
El perímetro para las nalgas se mide sobre estas:
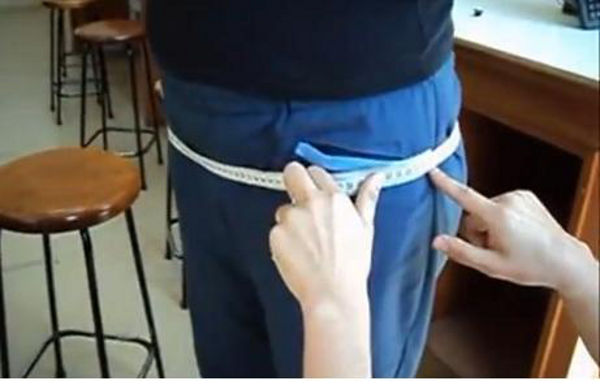
Perímetro mayor sobre nalgas
ID:(2129, 0)
Pectorales
Ejercicio 
Los pectorales se modela mediante semielipsoides con el semieje vertical
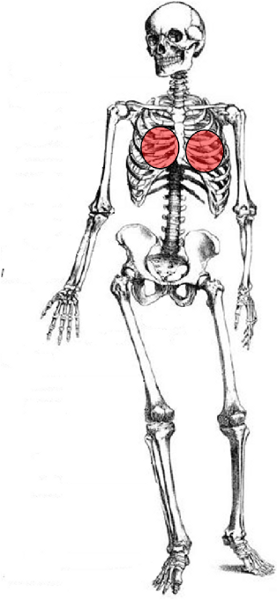
ID:(2138, 0)
Perímetro mayor sobre Pechos $s_9$
Ecuación 
El perímetro de los pechos se mide sobre éstos:

Perímetro mayor sobre pechos
ID:(2139, 0)
Modelar nalgas y pectorales
Storyboard 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Las nalgas y pectorales se modelan como mitades de elipsoides adosados a los conos truncados. Para ello se deben definir tanto las coordenadas del centro
En el caso de la cadera las posiciones en la altura coinciden con la altura de la cadera misma mientras que en los pectorales debemos alienarlos con la parte superior del t rax.
Las dimensiones se deben estimar determinando per metros o secciones de estos.
Como el centro de las nalgas deben de estar al centro de la cadera se tiene que:
Para que los pectorales queden en una posici n tal que su borde superior coincide con el del torax debemos primero estimar la altura de los hombros
y a ella restar el semieje vertical de los pectorales con lo que queda
Si se superponen las mitades de los elipsoides sobre los conos truncados y se mide el per metro la huincha de medir recorrer algo asi como la siguiente linea roja:
Entre nalgas/pectorales la hincha hace un puente (secci n superior), luego se adhiere a la nalga/pectoral para luego continuar tangencialmente de un cuerpo al otro. El resto del recorrido (espalda) es igual al per metro del cono truncado.
Las nalgas se modela mediante semielipsoides con el semieje vertical
El per metro para las nalgas se mide sobre estas:
Los pectorales se modela mediante semielipsoides con el semieje vertical
El per metro de los pechos se mide sobre stos:
Per metro mayor sobre pechos
Si se mide la fracci n del per metro que esta ocupado por nalgas y pectorales se esta estimando el doble del semieje
y asumiendo que el angulo es peque o con lo que la cuerda es similar a la rango del per metro se puede estimar el angulo
lo que en nuestro caso es
Para modelar las nalgas y pectorales se puede pensar en que cadera y t rax se pueden ver como un cilindro con un radio
Si se supone una base circular se puede asumir que el semieje horizontal tangencial al cuerpo
Si se observa la gr fica de la modelaci n de las nalgas y pectorales se ve que la distancia entre el centro del cono truncado y el centro del elipsoide es por Pit goras:
Como dicha distancia es la hipotenusa de un triangulo en que la distancia entre el centro del elipsoide y el eje vertical, que es la posici n
Si se observa la gr fica de la modelaci n de las nalgas y pectorales se ve que la distancia entre el centro del cono truncado y el centro del elipsoide es por Pit goras:
Como dicha distancia es la hipotenusa de un triangulo en que la distancia entre el centro del elipsoide y el eje horizontal, que es la posici n
El sector tangencial entre la nalga/pectoral y la cadera/t rax se puede estimar de la distancia entre el centro del cono truncado y el centro del elipsoide
y el angulo entre el radio y la linea del contacto de la huinca con el cono truncado
con lo que el segmento ser a
que transformando a coseno resulta un segmento
El angulo total que la huincha se adhiere al cuerpo es el radio medio
Con la relaci n del arco
se tiene una contribuci n
La secci n del per metro que recorre la superficie de nalgas/pectorales se puede calcular de la ecuaci n del arco
Como el angulo cubierto es el angulo recto menos el angulo
El per metro tiene varios segmentos que deben ser modelados por separado:
- sector horizontal entre nalgas/pectorales
- per metro sobre nalgas/pectorales
- puente entre nalgas/pectorales y cadera/t rax
- per metro sobre cadera/t rax
El primer elementos es igual a la coordenada
En el sector que recorre sobre las nalgas/pectorales se puede trabajar con el per metro
mientras que la parte tangencial es
y el resto del per metro seria
Si se suman los primeros segmentos en forma doble mas el cuarto y se igualan a el per metro medido
ID:(1353, 0)
