Druyd:Knowledge

Estructura del modelo

Storyboard

Cada parte geométrica debe especificarse en función de sus dimensiones físicas y posicionada en el espacio.

>Modelo

ID:(631, 0)

Perímetro y radio de un circulo

Definición

ID:(1630, 0)

Pesándose

Imagen

ID:(1632, 0)

Estructura del modelo

Descripción

Cada parte geométrica debe especificarse en función de sus dimensiones físicas y posicionada en el espacio.

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$c_i$

c_i

Altura del cilindro i

$c_i$

c_i

Altura del cono truncado i

$c_i$

c_i

Altura del paralelepípedo recto i

$b_i$

b_i

Ancho del paralelepípedo recto i

$\rho$

rho

Densidad del cuerpo

kg/m^3

$a_i$

a_i

Largo del paralelepípedo recto i

$M$

Masa

$s_a$

s_a

Perímetro alrededor del semieje a del elipsoide

$s_b$

s_b

Perímetro alrededor del semieje b del elipsoide

$s_c$

s_c

Perímetro alrededor del semieje c del elipsoide

$s$

Perímetro de una sección circular

$a_{15}$

a_15

Primer semieje de la cabeza (plano y-z)

$r$

Radio de un disco

$a_i$

a_i

Radio del cilindro i

$a_i$

a_i

Radio mayor del cono truncado i

$b_i$

b_i

Radio menor del cono truncado i

$b_{15}$

b_15

Segundo semieje de la cabeza (plano x-z)

$a$

Semieje a de un elipsoide

$b$

Semieje b de un elipsoide

$c$

Semieje c de un elipsoide

$b_i$

b_i

Semieje de la nalgas/pectorales perpendicular al cuerpo

$a_6$

a_6

Semieje horizontal de nalgas/pectorales

$b_6$

b_6

Semieje vertical de las nalgas/pectorales

$c_{15}$

c_15

Tercer semieje de la cabeza (plano x-y)

$V_{15}$

V_15

Volumen de la cabeza

m^3

$V_5$

V_5

Volumen de la cadera

m^3

$V_{12}$

V_12

Volumen de la mano

m^3

$V_3$

V_3

Volumen de la pierna

m^3

$V_{13}$

V_13

Volumen de los dedos de la mano

m^3

$V_2$

V_2

Volumen de los dedos del pie

m^3

$V_i$

V_i

Volumen de medio elipsoide

m^3

$V_9$

V_9

Volumen de un pectoral

m^3

$V_6$

V_6

Volumen de una nalga

m^3

$V_7$

V_7

Volumen del abdomen

m^3

$V_{11}$

V_11

Volumen del antebrazo

m^3

$V_{10}$

V_10

Volumen del brazo

m^3

$V_{c,i}$

V_ci

Volumen del cilindro i

m^3

$V_{o,i}$

V_oi

Volumen del cono truncado i

m^3

$V_{14}$

V_14

Volumen del cuello

m^3

$V_t$

V_t

Volumen del cuerpo

m^3

$V_4$

V_4

Volumen del muslo

m^3

$V_{p,i}$

V_pi

Volumen del paralelepípedo recto i

m^3

$V_1$

V_1

Volumen del pie

m^3

$V_8$

V_8

Volumen del tórax

m^3

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$ r =\displaystyle\displaystyle\frac{ s }{2 \pi }$

r = s /(2* pi )

(ID 4263)

$V_t=\sum_iV_i$

V_t=sum_i V_i

(ID 4264)

$M=\rho V$

M=rho*V

(ID 4265)

$a=\displaystyle\displaystyle\frac{1}{2^{3/2}\pi}\sqrt{s_b^2+s_c^2-s_a^2}$

a =sqrt( s_b ^2+ s_c ^2- s_a ^2)/(2^(3/2)* pi )

(ID 10477)

$b=\displaystyle\displaystyle\frac{1}{2^{3/2}\pi}\sqrt{s_a^2+s_c^2-s_b^2}$

b=sqrt(s_a^2+s_c^2-s_b^2)/(2^(3/2)*pi)

(ID 10478)

$c=\displaystyle\displaystyle\frac{1}{2^{3/2}\pi}\sqrt{s_a^2+s_b^2-s_c^2}$

c=sqrt(s_a^2+s_b^2-s_c^2)/(2^(3/2)*pi)

(ID 10479)

$V_{15}=\displaystyle\displaystyle\frac{4\pi}{3}a_{15}b_{15}c_{15}$

V_15=4*pi*a_15*b_15*c_15/3

(ID 10480)

$ V_i = \pi a_i ^2 c_i $

V_i = pi * a_i ^2 * c_i

(ID 10481)

$V_i=\displaystyle\frac{1}{3}\pi (a_i^2+a_ib_i+b_i^2) c_i$

V_i=pi*(a_i^2+a_i*b_i+b_i^2)*c_i

(ID 10482)

$V_i=a_ib_ic_i$

V_i=a_ib_ic_i

(ID 10483)

$V_i=\displaystyle\displaystyle\frac{2\pi}{3}a_ib_ic_i$

V_i=2*pi*a_i*b_i*c_i/3

(ID 10530)

Ejemplos

Per metro y radio de un circulo

Uno de los problemas en medir el radio de una parte de nuestro cuerpo es que no tenemos acceso a la secci n de los cuerpos. Por otro lado no son perfectamente circulares por lo que se necesita un valor medio del radio.

Una forma simple de estimar el radio es por ello midiendo el per metro que es igual a dos veces pi por el radio. Por ello basta con medir el per metro y dividirlo por 2\pi:

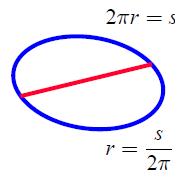
Per metro y radio de un circulo

Es importante tener claro que toda medici n tiene un limite de exactitud que esta dada por el instrumento que usamos. En el caso de la huincha la escala es milim trica y los largos medidos tienen como precisi n el mil metro. Esto tambi n aplica a el radio que se calcula que no tendr una mayor precisi n que la escala con que se midi el per metro, es decir el mil metro. Esto independiente de todas los decimales que llegara a indicar la calculadora con la que se dividi el per metro por dos pi.

(ID 1630)

Pes ndose

Para poder determinar que el modelo esta correctamente estructurado procedemos a pesarnos y comparar el valor medido con aquel que se calcula.

Pesa

(ID 1632)

ID:(631, 0)