Position dans une dimension
Storyboard 
Pour définir la position d'un objet, un système de coordonnées est introduit, ce qui permet d'établir un point d'origine et de définir la position en mesurant la distance le long d'une ligne droite ou d'une courbe. Par conséquent, l'unité de position correspond à une mesure de longueur, telle que les kilomètres, les mètres, les centimètres, et ainsi de suite.Le choix du système de coordonnées est flexible et est fait pour simplifier autant que possible la modélisation et les calculs associés. Par exemple, si l'objet se déplace le long d'une piste, qui n'est pas nécessairement droite, il est avantageux de définir le système de coordonnées le long de cette piste. Dans ce cas spécifique, la position est définie comme la distance depuis l'origine ou le point de départ de la piste.
ID:(607, 0)
Position, une dimension
Simulation 
Lun des aspects fondamentaux de la physique consiste à déterminer la position des objets que lon étudie. Ce simulateur permet dexplorer ce concept : en générant une barre rouge et en déplaçant la souris, on peut déterminer sa longueur. Cette longueur correspond à la position de son bord droit par rapport à une origine située au bord gauche.
Mesure de la taille de la boîte rouge
Créez une boîte rouge en cliquant sur le bouton situé sous la règle. Ensuite, faites-la glisser en maintenant le bouton gauche de la souris enfoncé jusqu'à aligner le zéro avec le bord gauche de la boîte. Lisez la valeur au niveau du bord droit, saisissez-la dans le champ ci-dessous, puis cliquez sur le bouton pour vérifier si la mesure est correcte.Considérez le panneau du simulateur :
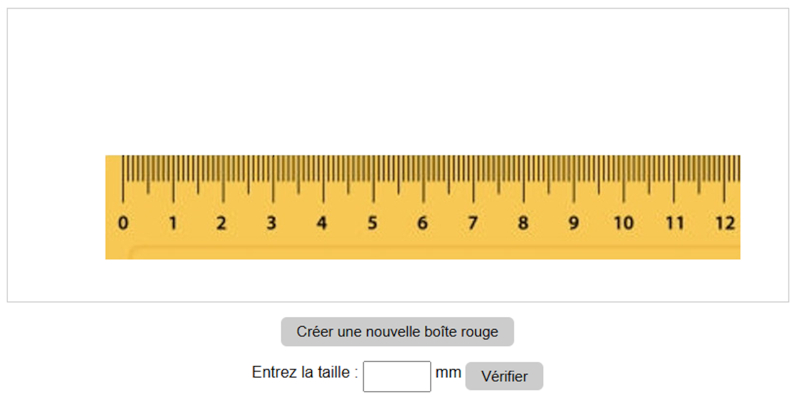
Créez une boîte rouge en appuyant sur le bouton situé sous la règle.
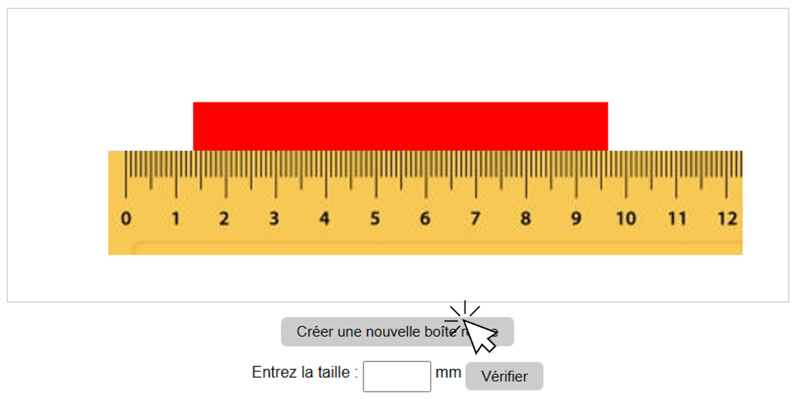
Ensuite, faites-la glisser en maintenant le bouton gauche de la souris enfoncé.
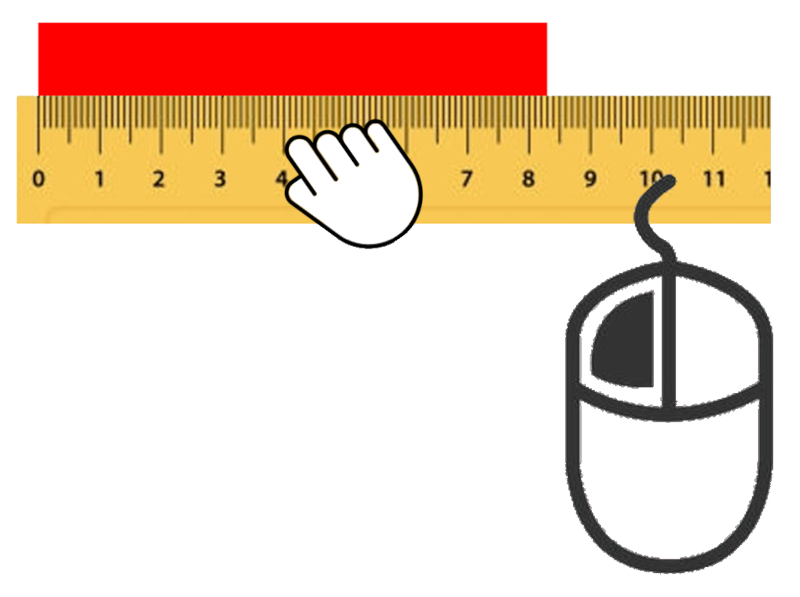
Assurez-vous quelle soit bien alignée avec le zéro de la règle au bord gauche de la boîte.

Lisez la valeur indiquée au bord droit.

Saisissez la valeur estimée dans le champ inférieur (les valeurs fractionnaires sont acceptées).

Si la valeur est correcte, une confirmation s'affichera. En cas d'erreur, la valeur exacte sera indiquée.

Vous pouvez expérimenter en déplaçant lorigine vers la gauche et observer comment un léger décalage initial peut fausser le résultat final. Vous pouvez également ajuster la valeur saisie elle sera considérée comme correcte si elle se situe dans une marge dun millimètre.
Si quelquun nous dit que sa position est à 45km, la première question qui se pose est: à partir doù? Autrement dit, il est essentiel de connaître lorigine à partir de laquelle cette indication prend sens.
Dans le simulateur, cela signifie quil faut placer le zéro de la règle au bord gauche de la boîte rouge pour pouvoir déterminer correctement la position du bord droit.

Si cela nest pas fait avec précision, la valeur lue à droite sera incorrecte et la simulation indiquera que la mesure a été mal effectuée :

En plaçant la règle à l'origine, on se rend immédiatement compte quil est difficile daligner précisément le zéro avec le bord gauche. Une situation similaire se produit au bord droit, qui tombe entre deux graduations de la règle, nous obligeant à estimer sa valeur :

Finalement, nous estimons la fraction de lespace couvert et donnons une valeur avec une précision dun dixième de millimètre. Cela nous fait prendre conscience que nous travaillons à léchelle du dixième sans même nous soucier des centièmes.Nous en concluons donc que tout instrument de mesure (pas seulement ceux qui mesurent des longueurs) comporte une limitation inhérente. Pour cette raison, les valeurs issues d'une mesure doivent toujours être accompagnées de leur incertitude. Cela peut être indiqué en associant le nombre à une plage, par exemple : [27,1 ; 27,7], ou en utilisant la valeur moyenne (27,4) et en précisant combien il faut ajouter ou soustraire pour obtenir lintervalle :27,4±0,3Ce principe sapplique non seulement à chaque mesure individuelle, mais aussi au calcul de distances, comme le montre le modèle à travers un exemple.
ID:(3, 0)
Référence de mesure de longueur
Description 
Chaque mesure correspond à une comparaison d'une valeur spécifique avec un modèle de référence, ce qui donne la valeur dans l'unité correspondante.
Au fil du temps, ces modèles ont évolué, atteignant une précision accrue. Les exemples incluent :

Fausse copie du premier étalon de mètre (notez l'orthographe incorrecte), scellée dans les fondations d'un immeuble, 36 rue de Vaugirard, Paris, Ken Eckert (Wikimedia Commons)
Une copie du mètre provisoire installé de 1796 à 1797, située sur le mur d'un bâtiment au 36 rue de Vaugirard, à Paris

Répliques historiques néerlandaises d'étalons métriques dans la collection du Rijksmuseum d'Amsterdam : mètre en fer avec étui (construit par Étienne Lenoir, 1799; numéro de catalogue NG-2001-16-C-8), kilogramme funéraire en cuivre avec étui (1798; numéro de catalogue NG-2001-16-D-9), mesures de volume en cuivre ( 1829 ; numéro de catalogue NG-2001-16-B-28)., Yerpo (Wikimedia Commons)
En 1799, Étienne Lenoir a fabriqué les normes de platine et douze de fer du mètre.

Rule (Modifié à partir de Wikimedia Commons, Une règle, représentant deux unités habituelles de longueur, le centimètre et le pouce)
La règle graduée comprend une échelle graduée longitudinale en acier inoxydable pour éviter que la formation de rouille n'entrave la lecture ou n'efface l'échelle.
ID:(2238, 0)
Règle ou ruban à mesurer
Description 
Une règle ou un mètre ruban sont tous deux des méthodes de mesure de la longueur. Une règle est un dispositif de mesure plat marqué avec des unités de longueur telles que des pouces, des centimètres ou des millimètres. Un mètre ruban est un dispositif de mesure souple marqué avec des unités de longueur. Les mètres rubans sont généralement plus précis que les règles, car ils peuvent mesurer des surfaces courbes et peuvent être étendus à des longueurs plus grandes.

ID:(12508, 0)
Télémètre laser
Description 
Un télémètre laser est un dispositif qui utilise un faisceau laser pour mesurer la distance entre deux points. Il fonctionne en envoyant un pulse laser, qui est réfléchi par l'objet mesuré et ensuite détecté par le télémètre laser. Le temps qu'il faut au pulse laser pour aller du télémètre laser à l'objet et retour peut alors être utilisé pour calculer la distance entre les deux points. Les télémètres laser sont couramment utilisés dans le cadre de levés topographiques, de navigation et d'autres applications où des mesures précises sont nécessaires.

ID:(481, 0)
GPS (Système de positionnement global)
Description 
Le système de positionnement global (GPS) est un système de navigation par satellite qui utilise un réseau de 24 satellites orbitant autour de la Terre pour déterminer l'emplacement exact d'une personne ou d'un objet sur la planète. Les récepteurs GPS calculent la distance à chaque satellite en mesurant le temps qu\'il faut aux signaux pour voyager du satellite au récepteur. Une fois ces distances connues, le récepteur peut utiliser un processus appelé trilatération pour calculer sa position exacte, y compris la longitude et la latitude, ainsi que l\'altitude. Cela peut être utilisé pour mesurer les distances entre deux emplacements, ainsi que la longueur d\'un chemin parcouru par une personne ou un objet.

ID:(474, 0)
Position
Description 
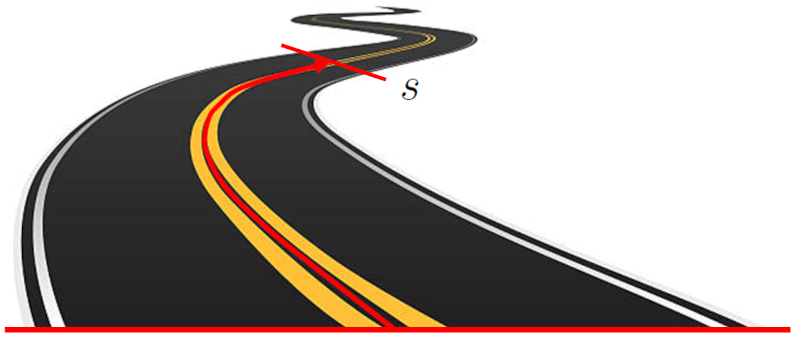
A position ($s$) d'un objet dans un système unidimensionnel fait référence à l'emplacement de l\'objet par rapport à un point de référence. Cette position est exprimée comme la distance entre l\'objet et le point d\'origine. Cette distance peut être une ligne droite sur un axe cartésien, ou elle peut suivre un chemin courbe.
ID:(15, 0)
Position initiale
Description 
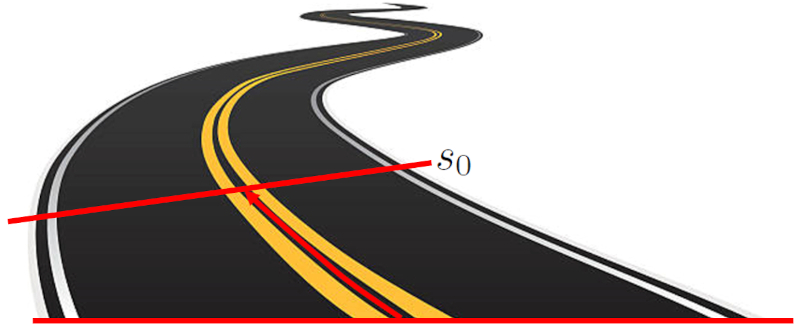
A vitesse ($s_0$) est l'emplacement de départ d'un objet avant que tout mouvement ne commence. Cette position est définie comme la distance entre l\'objet et le point d\'origine. Cette distance peut être une ligne droite sur un axe cartésien ou elle peut suivre une trajectoire courbe.
ID:(10302, 0)
Distance parcourue
Description 
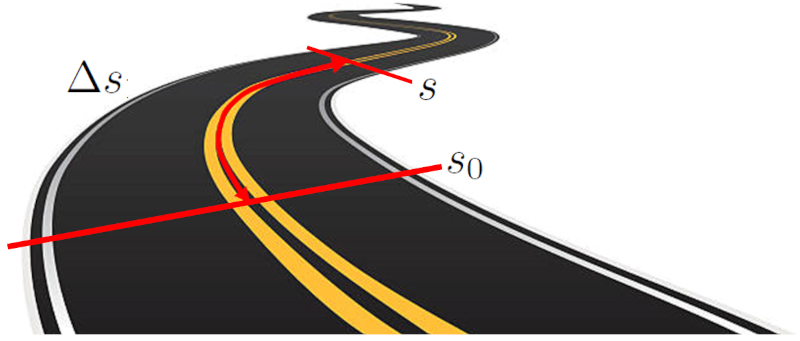
A distance parcourue en un temps ($\Delta s$) par un objet est mesurée en mesurant la distance entre deux points spécifiques le long d'une trajectoire. Cette trajectoire peut être une ligne droite sur un axe cartésien ou un chemin courbe. La distance est calculée en mesurant la longueur de la trajectoire entre les deux points de départ et d'arrivée.
ID:(9495, 0)
Position dans une dimension
Modèle 
Pour définir la position d'un objet, un système de coordonnées est introduit, ce qui permet d'établir un point d'origine et de définir la position en mesurant la distance le long d'une ligne droite ou d'une courbe. Par conséquent, l'unité de position correspond à une mesure de longueur, telle que les kilomètres, les mètres, les centimètres, et ainsi de suite. Le choix du système de coordonnées est flexible et est fait pour simplifier autant que possible la modélisation et les calculs associés. Par exemple, si l'objet se déplace le long d'une piste, qui n'est pas nécessairement droite, il est avantageux de définir le système de coordonnées le long de cette piste. Dans ce cas spécifique, la position est définie comme la distance depuis l'origine ou le point de départ de la piste.
Variables
Calculs
Calculs
Équations
Si l’on part de a vitesse ($s_0$) et que l’on souhaite calculer a distance parcourue en un temps ($\Delta s$), il est nécessaire de définir une valeur pour a position ($s$).
Dans un système unidimensionnel, a distance parcourue en un temps ($\Delta s$) est simplement obtenu en soustrayant a vitesse ($s_0$) de a position ($s$), ce qui donne :
| $ \Delta s = s - s_0 $ |
(ID 4352)
Exemples
A distance infinitésimale parcourue ($ds$) entre deux points est une mesure de distance si petite que le mouvement entre les deux points peut tre consid r comme uniforme.
G n ralement, les diff rences d'une variable sont not es en ajoutant le symbole $\Delta$ avant la lettre correspondante, de sorte que la variation de la position $s$ est repr sent e comme $\Delta s$. Pour les variations infinit simales, on utilise un $d$ la place de $\Delta$, ainsi une variation infinit simale de la position serait repr sent e comme $ds$.
(ID 14451)
Pour mod liser le mouvement d'un corps, il est n cessaire de d crire comment il se d place, c'est- -dire le chemin et la direction dans lesquels il se d place. Si le chemin est courb , le vecteur entre la position actuelle et future ne correspondra pas n cessairement au chemin r el, sauf si le chemin est infinit simal. Dans ce cas, la d viation du segment est n gligeable et l\'arc correspond au vecteur tangentiel de la courbe.
(ID 14452)
En physique, la position fait r f rence l'emplacement d'un objet dans l\'espace par rapport un point de r f rence ou un origine. C\'est un concept fondamental qui est utilis pour d crire le mouvement des objets et est souvent repr sent comme une grandeur vectorielle avec une magnitude et une direction.La position peut tre d crite en utilisant un syst me de coordonn es, tel qu\'un syst me de coordonn es cart siennes, qui utilise trois axes (x, y et z) pour d finir la position d\'un objet dans l\'espace tridimensionnel. La position d\'un objet peut tre mesur e et exprim e en unit s de longueur, telles que les m tres, les pieds ou les kilom tres.Le changement de la position d\'un objet au fil du temps est appel d placement, qui est galement une grandeur vectorielle qui prend en compte la direction du mouvement de l\'objet. La position, le d placement et d\'autres concepts connexes sont au centre de l\' tude de la m canique, qui est une branche de la physique qui traite du mouvement des objets et des forces qui causent ce mouvement.
(ID 14449)
ID:(607, 0)
