Position in one dimension
Storyboard 
To define the position of an object, a coordinate system is introduced that allows establishing an origin point and defining the position by measuring the distance along a straight line or a curve. As a result, the unit of position corresponds to a length measurement, such as kilometers, meters, centimeters, and so on.The choice of the coordinate system is flexible and is made to simplify the modeling and associated calculations as much as possible. For instance, if the object moves along a track, which may not necessarily be straight, it is advantageous to define the coordinate system along that track. In this specific case, the position is defined as the distance from the origin or the starting point of the track.
ID:(607, 0)
Position, a dimension
Simulation 
One of the fundamental aspects of physics is determining the position of the objects we analyze. This simulator allows you to explore that concept: by generating a red bar and moving the mouse, you can determine its length. This length corresponds to the position of its right edge relative to an origin located at the left edge.
Measuring the size of the red box
Create a red box by clicking the button below the ruler. Then, drag it while holding down the left mouse button until the zero aligns with the left edge of the box. Read the value at the right edge, enter it in the field below, and press the button to check if the measurement is correct.Consider the simulator panel:
Create a red box by pressing the button located below the ruler.
Then, drag it while holding down the left mouse button.
Make sure it is correctly aligned with the zero on the ruler at the left edge of the box.

Read the value shown at the right edge.

Enter the estimated value in the input field below (fractional values are allowed).
If the value is correct, a confirmation will be shown. If it is incorrect, the correct value will be displayed.
You can experiment by shifting the origin to the left and observe how a small misalignment leads to an error in the final result. You can also adjust the entered value it will be considered correct as long as it is within a one-millimeter margin.
If someone tells us their location is 45 km, we are immediately compelled to ask: from where? In other words, we need to know the origin that gives meaning to that information.
In the simulator, this means we must place the zero of the ruler at the left edge of the red box to correctly determine the position of the right edge.

If it is not positioned carefully, the value we read on the ruler at the right edge will be incorrect, and the simulation will show us that we have measured incorrectly:
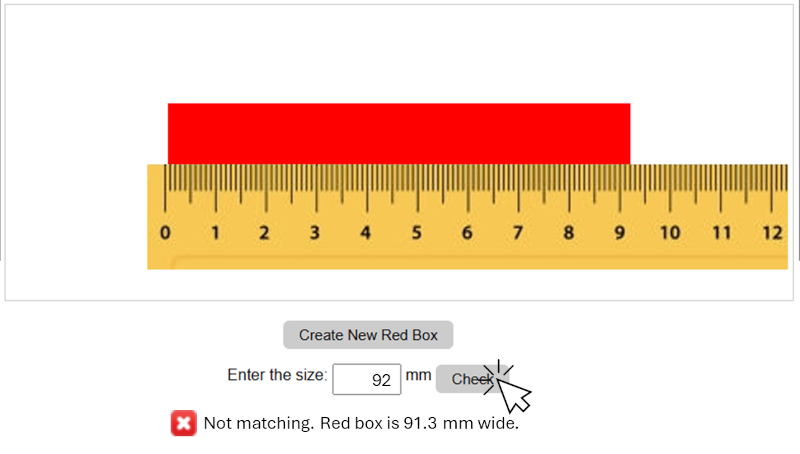
When we place the ruler at the origin, we immediately realize how difficult it is to align the zero precisely with the left edge. A similar issue arises on the right edge, where it falls between two marks on the ruler, and we are forced to estimate its corresponding value:

In the end, we estimate the fraction of space covered and assign a value in tenths of a millimeter. However, we come to realize that we are operating at a scale of tenths of millimeters without even considering hundredths.Therefore, we conclude that every measuring instrument (not just those for length) has an inherent limitation. For this reason, the values obtained from a measurement should always be expressed along with their uncertainty. This can be indicated by associating the number with a range, for example: [27.1, 27.7], or by using the average value (27.4) and specifying how much to add or subtract to obtain the range:27.4±0.3This principle applies not only to individual measurements but also to the calculation of distances, as demonstrated in the model with an example.
ID:(3, 0)
Length measurement reference
Description 
Each measurement corresponds to a comparison of a specific value and a reference pattern, resulting in the value being obtained in the corresponding unit.
Over time, these patterns have evolved, achieving greater accuracy. Examples include:

Fake copy of the first metre standard (notice the incorrect spelling), sealed in the foundation of a building, 36 rue de Vaugirard, Paris, Ken Eckert (Wikimedia Commons)
A copy of the provisional meter installed from 1796 to 1797, located on the wall of a building at 36 rue de Vaugirard, Paris

Historic Dutch replicas of metric standards in the collection of Rijksmuseum, Amsterdam: iron metre with case (constructed by Étienne Lenoir, 1799; catalog number NG-2001-16-C-8), copper grave kilogram with case (1798; catalog number NG-2001-16-D-9), copper volume measures (1829; catalog number NG-2001-16-B-28)., Yerpo (Wikimedia Commons)
In 1799, Étienne Lenoir fabricated the platinum and twelve iron standards of the meter.

Rule (Modified from Wikimedia Commons, A ruler, depicting two customary units of length, the centimetre and the inch)
The graduated ruler includes a longitudinal graduated scale made of stainless steel to prevent rust formation from hindering reading or erasing the scale.
ID:(2238, 0)
Ruler or Tape Measure
Description 
Ruler or Tape Measure are both methods of measuring length. A ruler is a flat measuring device that is marked with units of length such as inches, centimeters or millimeters. A tape measure is a flexible measuring device that is marked with units of length. Tape measures are usually more accurate than rulers, as they can measure curved surfaces and can be extended to greater lengths.

ID:(12508, 0)
Laser rangefinder
Description 
A laser rangefinder is a device that uses a laser beam to measure the distance between two points. It works by sending out a laser pulse, which is reflected off of the object being measured and then detected by the rangefinder. The time it takes for the laser pulse to travel from the rangefinder to the object and back can then be used to calculate the distance between the two points. Laser rangefinders are commonly used in surveying, navigation, and other applications where precise measurements are needed.

ID:(481, 0)
GPS (Global Positioning System)
Description 
The Global Positioning System (GPS) is a satellite-based navigation system that uses a network of 24 satellites orbiting the Earth to determine the exact location of a person or object on the planet. GPS receivers calculate the distance to each satellite by measuring the amount of time it takes for signals to travel from the satellite to the receiver. Once these distances are known, the receiver can use a process called trilateration to calculate its exact location, including longitude and latitude, as well as altitude. This can be used to measure distances between two locations, as well as the length of a path taken by a person or object.

ID:(474, 0)
Position
Description 
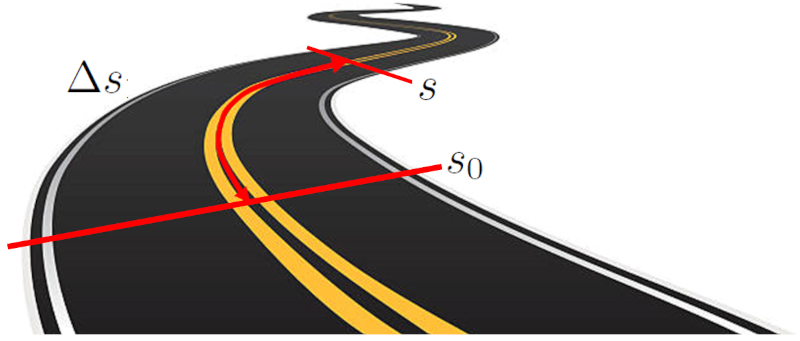
The position ($s$) of an object in a one-dimensional system refers to the location of the object in relation to a reference point. This location is expressed as the distance between the object and the origin point. This distance can be a straight line on a Cartesian axis, or it can follow a curved path:
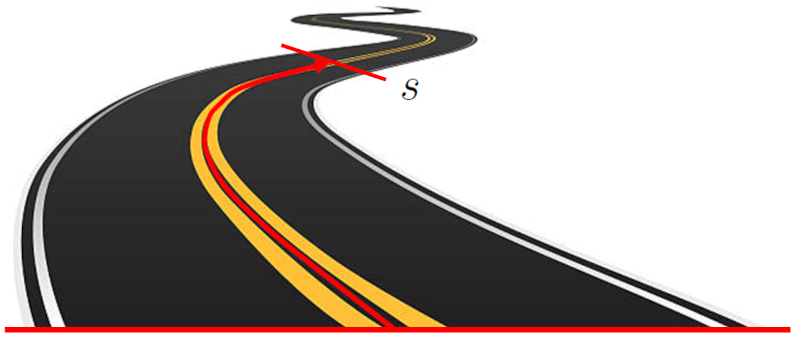
ID:(15, 0)
Initial position
Description 
The starting position ($s_0$) is the starting location of an object before any motion begins. This location is defined as the distance between the object and the origin point. This distance can be a straight line on a Cartesian axis or it can follow a curved path.
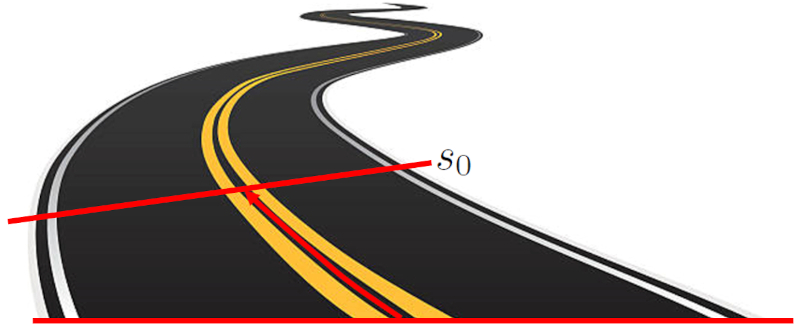
ID:(10302, 0)
Distance traveled
Description 
The distance traveled in a time ($\Delta s$) by an object is measured by measuring the distance between two specific points along a trajectory. This trajectory can be a straight line on a Cartesian axis or a curved path. The distance is calculated by measuring the length of the trajectory between the two starting and ending points.
ID:(9495, 0)
Position in one dimension
Model 
To define the position of an object, a coordinate system is introduced that allows establishing an origin point and defining the position by measuring the distance along a straight line or a curve. As a result, the unit of position corresponds to a length measurement, such as kilometers, meters, centimeters, and so on. The choice of the coordinate system is flexible and is made to simplify the modeling and associated calculations as much as possible. For instance, if the object moves along a track, which may not necessarily be straight, it is advantageous to define the coordinate system along that track. In this specific case, the position is defined as the distance from the origin or the starting point of the track.
Variables
Calculations
Calculations
Equations
If we start from the starting position ($s_0$) and want to calculate the distance traveled in a time ($\Delta s$), we need to define a value for the position ($s$).
In a one-dimensional system, the distance traveled in a time ($\Delta s$) is simply obtained by subtracting the starting position ($s_0$) from the position ($s$), resulting in:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Examples
In physics, position refers to an object's location in space relative to a reference point or origin. It is a fundamental concept that is used to describe the motion of objects, and is often represented as a vector quantity with magnitude and direction.Position can be described using a coordinate system, such as a Cartesian coordinate system, which uses three axes (x, y, and z) to define the position of an object in three-dimensional space. The position of an object can be measured and expressed in units of length, such as meters, feet, or kilometers.The change in an object's position over time is known as displacement, which is also a vector quantity that takes into account the object\'s direction of motion. Position, displacement, and other related concepts are central to the study of mechanics, which is a branch of physics that deals with the motion of objects and the forces that cause that motion.
(ID 14449)
The infinitesimal distance traveled ($ds$) between two points is a measurement so small that the motion between them can be considered uniform, or in other words, at constant velocity.
Generally, differences of a variable are denoted by adding the symbol $\Delta$ before the corresponding letter, so the variation in position $s$ is represented as $\Delta s$. For infinitesimal variations, a $d$ is used instead of $\Delta$, thus an infinitesimal variation in position would be represented as $ds$.
(ID 14451)
To model the motion of a body, it is necessary to describe how it moves, that is, the path and the direction in which it moves. If the path is curved, the vector between the current and future position may not necessarily coincide with the actual path, unless the path is infinitesimal. In such a case, the deviation from the segment is negligible, and the arc corresponds to the tangential vector of the curve.
(ID 14452)
ID:(607, 0)
