Aceleración constante, dos etapas
Storyboard 
En el caso de un movimiento acelerado en dos etapas, en el momento en que se pasa de la primera a la segunda aceleración, la velocidad final de la primera etapa se convierte en la velocidad inicial de la segunda. Lo mismo ocurre con la posición, donde la posición final de la primera etapa es igual a la posición inicial de la segunda etapa.
A diferencia del modelo de dos velocidades, este modelo no presenta problemas de discontinuidad, excepto que la aceleración puede cambiar de forma abrupta, lo cual es técnicamente posible aunque muchas veces no tan realista.
ID:(1435, 0)
Movimiento en dos etapas
Imagen 
En un escenario de movimiento en dos etapas, primero el objeto modifica su velocidad en la diferencia de velocidad en la primera etapa ($\Delta v_1$) durante un lapso de tiempo de un tiempo transcurrido en la primera etapa ($\Delta t_1$) con una aceleración de una aceleración durante la primera etapa ($a_1$).
| $ a_1 \equiv\displaystyle\frac{ \Delta v_1 }{ \Delta t_1 }$ |
Posteriormente, en la segunda etapa, avanza modificando su velocidad en la diferencia de velocidad en la segunda etapa ($\Delta v_2$) durante un lapso de tiempo de el tiempo transcurrido en la segunda etapa ($\Delta t_2$) con una aceleración de la aceleración durante la segunda etapa ($a_2$).
| $ a_2 \equiv\displaystyle\frac{ \Delta v_2 }{ \Delta t_2 }$ |
Al representar esto gráficamente, obtenemos un diagrama de velocidad y tiempo como se muestra a continuación:
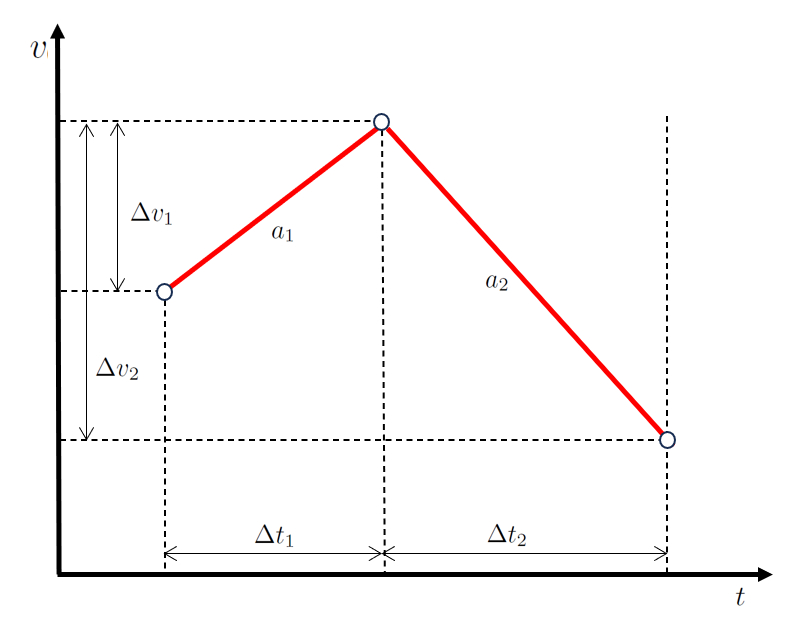
La clave aquí es que los valores el tiempo transcurrido en la primera etapa ($\Delta t_1$) y el tiempo transcurrido en la segunda etapa ($\Delta t_2$) son secuenciales, al igual que los valores la diferencia de velocidad en la primera etapa ($\Delta v_1$) y la diferencia de velocidad en la segunda etapa ($\Delta v_2$).
ID:(4829, 0)
Evolución de la velocidad
Nota 
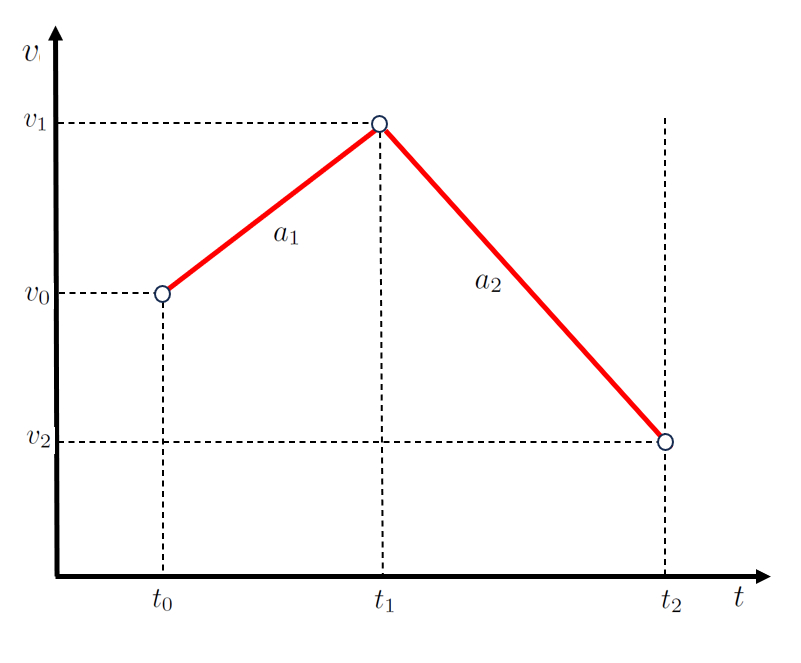
En el caso de un movimiento en dos etapas, la primera etapa se puede describir mediante una función que involucra los puntos el tiempo inicial ($t_0$), el tiempo final primera e inició segunda etapa ($t_1$), la velocidad inicial ($v_0$) y la velocidad primera etapa ($v_1$), representada por una recta con pendiente de la aceleración durante la primera etapa ($a_1$):
| $ v_1 = v_0 + a_1 ( t_1 - t_0 )$ |
Para la segunda etapa, definida por los puntos la velocidad primera etapa ($v_1$), la velocidad segunda etapa ($v_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), se emplea una segunda recta con pendiente de la aceleración durante la segunda etapa ($a_2$):
| $ v_2 = v_1 + a_2 ( t_2 - t_1 )$ |
que se representa como:
ID:(4357, 0)
Evolución de la posición
Cita 
En el caso de un movimiento en dos etapas, la posición en la que termina la primera etapa coincide con la posición del inicio de la segunda etapa ($s_1$).
Del mismo modo, el tiempo en que termina la primera etapa coincide con el tiempo de inicio de la segunda etapa ($t_1$).
Dado que el movimiento se define según la aceleración experimentada, la velocidad alcanzada al final de la primera etapa debe coincidir con la velocidad inicial de la segunda etapa ($v_1$).
En el caso de una aceleración constante, en la primera etapa, el posición final primera e inició segunda etapa ($s_1$) depende de la posición inicial ($s_0$), la velocidad inicial ($v_0$), la aceleración durante la primera etapa ($a_1$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo inicial ($t_0$), según:
| $ s_1 = s_0 + v_0 ( t_1 - t_0 )+\displaystyle\frac{1}{2} a_1 ( t_1 - t_0 )^2$ |
En la segunda etapa, la posición final segunda etapa ($s_2$) depende de el posición final primera e inició segunda etapa ($s_1$), la velocidad primera etapa ($v_1$), la aceleración durante la segunda etapa ($a_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), según:
| $ s_2 = s_1 + v_1 ( t_2 - t_1 )+\displaystyle\frac{1}{2} a_2 ( t_2 - t_1 )^2$ |
que se representa como:
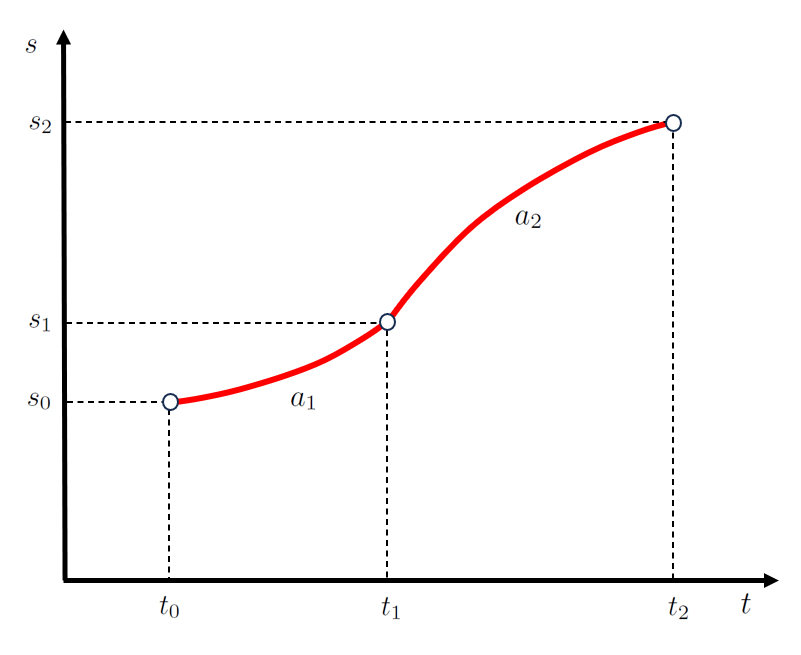
Área bajo la curva aceleración constante
ID:(2254, 0)
Modelo
Ejercicio 
Si el movimiento consiste en dos etapas con diferentes aceleraciones constantes $a_1$ y $a_2$:
• Comienza en un tiempo $t_0$ en una posición $s_0$ y velocidad $v_0$.
• Termina el movimiento en un tiempo $t_2$ en una posición $s_2$ y velocidad $v_2$.
La clave reside en el proceso de transición de una etapa a otra:
• Las velocidades varían según las aceleraciones pero son iguales en el punto de transición entre etapas ($v_1$).
• Las posiciones varían según la velocidad pero son iguales en el punto de transición entre etapas ($s_1$).
• Los tiempos son iguales en el punto de transición entre etapas ($t_1$).
Esto se resume en las siguientes gráficas:

Las ecuaciones que cumplen estas relaciones dan origen al siguiente modelo que permite calcular cualquier escenario:
ID:(15400, 0)
Aceleración constante, dos etapas
Storyboard 
En el caso de un movimiento acelerado en dos etapas, en el momento en que se pasa de la primera a la segunda aceleración, la velocidad final de la primera etapa se convierte en la velocidad inicial de la segunda. Lo mismo ocurre con la posición, donde la posición final de la primera etapa es igual a la posición inicial de la segunda etapa. A diferencia del modelo de dos velocidades, este modelo no presenta problemas de discontinuidad, excepto que la aceleración puede cambiar de forma abrupta, lo cual es técnicamente posible aunque muchas veces no tan realista.
Variables
Cálculos
Cálculos
Ecuaciones
En el caso de que la aceleración constante ($a_0$) sea igual a la aceleración media ($\bar{a}$), ser igual a
Por lo tanto, considerando la diferencia de velocidad ($\Delta v$)
y el tiempo transcurrido ($\Delta t$)
la ecuaci n de la aceleración constante ($a_0$)
se puede escribir como
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
y al despejar, se obtiene
En el caso de que la aceleración constante ($a_0$) sea igual a la aceleración media ($\bar{a}$), ser igual a
Por lo tanto, considerando la diferencia de velocidad ($\Delta v$)
y el tiempo transcurrido ($\Delta t$)
la ecuaci n de la aceleración constante ($a_0$)
se puede escribir como
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
y al despejar, se obtiene
En el caso de la aceleración constante ($a_0$), la velocidad ($v$) en funci n de el tiempo ($t$) es una recta que pasa por el tiempo inicial ($t_0$) y la velocidad inicial ($v_0$), definida por la ecuaci n:
Dado que la distancia recorrida en un tiempo ($\Delta s$) representa el rea bajo la curva velocidad-tiempo, podemos sumar las contribuciones del rect ngulo:
$v_0(t-t_0)$
y el tri ngulo:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Para obtener la distancia recorrida en un tiempo ($\Delta s$) con la posición ($s$) y la posición inicial ($s_0$), resultando en:
Por lo tanto:
En el caso de la aceleración constante ($a_0$), la velocidad ($v$) en funci n de el tiempo ($t$) es una recta que pasa por el tiempo inicial ($t_0$) y la velocidad inicial ($v_0$), definida por la ecuaci n:
Dado que la distancia recorrida en un tiempo ($\Delta s$) representa el rea bajo la curva velocidad-tiempo, podemos sumar las contribuciones del rect ngulo:
$v_0(t-t_0)$
y el tri ngulo:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Para obtener la distancia recorrida en un tiempo ($\Delta s$) con la posición ($s$) y la posición inicial ($s_0$), resultando en:
Por lo tanto:
Si despejamos las ecuaciones para el tiempo ($t$) y el tiempo inicial ($t_0$) en la ecuaci n de la velocidad ($v$), que depende de la velocidad inicial ($v_0$) y la aceleración constante ($a_0$):
obtenemos:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Y al sustituir esto en la ecuaci n de la posición ($s$) con la posición inicial ($s_0$):
obtenemos una expresi n para el camino recorrido en funci n de la velocidad:
Si despejamos las ecuaciones para el tiempo ($t$) y el tiempo inicial ($t_0$) en la ecuaci n de la velocidad ($v$), que depende de la velocidad inicial ($v_0$) y la aceleración constante ($a_0$):
obtenemos:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Y al sustituir esto en la ecuaci n de la posición ($s$) con la posición inicial ($s_0$):
obtenemos una expresi n para el camino recorrido en funci n de la velocidad:
La definici n de la aceleración media ($\bar{a}$) se considera como la relaci n entre la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$). Es decir,
y
Se define la relaci n entre ambos como la aceleración centrifuga ($a_c$)
en dicho intervalo de tiempo.
La definici n de la aceleración media ($\bar{a}$) se considera como la relaci n entre la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$). Es decir,
y
Se define la relaci n entre ambos como la aceleración centrifuga ($a_c$)
en dicho intervalo de tiempo.
Ejemplos
En un escenario de movimiento en dos etapas, primero el objeto modifica su velocidad en la diferencia de velocidad en la primera etapa ($\Delta v_1$) durante un lapso de tiempo de un tiempo transcurrido en la primera etapa ($\Delta t_1$) con una aceleraci n de una aceleración durante la primera etapa ($a_1$).
Posteriormente, en la segunda etapa, avanza modificando su velocidad en la diferencia de velocidad en la segunda etapa ($\Delta v_2$) durante un lapso de tiempo de el tiempo transcurrido en la segunda etapa ($\Delta t_2$) con una aceleraci n de la aceleración durante la segunda etapa ($a_2$).
Al representar esto gr ficamente, obtenemos un diagrama de velocidad y tiempo como se muestra a continuaci n:
La clave aqu es que los valores el tiempo transcurrido en la primera etapa ($\Delta t_1$) y el tiempo transcurrido en la segunda etapa ($\Delta t_2$) son secuenciales, al igual que los valores la diferencia de velocidad en la primera etapa ($\Delta v_1$) y la diferencia de velocidad en la segunda etapa ($\Delta v_2$).
En el caso de un movimiento en dos etapas, la primera etapa se puede describir mediante una funci n que involucra los puntos el tiempo inicial ($t_0$), el tiempo final primera e inició segunda etapa ($t_1$), la velocidad inicial ($v_0$) y la velocidad primera etapa ($v_1$), representada por una recta con pendiente de la aceleración durante la primera etapa ($a_1$):
Para la segunda etapa, definida por los puntos la velocidad primera etapa ($v_1$), la velocidad segunda etapa ($v_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), se emplea una segunda recta con pendiente de la aceleración durante la segunda etapa ($a_2$):
que se representa como:
En el caso de un movimiento en dos etapas, la posici n en la que termina la primera etapa coincide con la posici n del inicio de la segunda etapa ($s_1$).
Del mismo modo, el tiempo en que termina la primera etapa coincide con el tiempo de inicio de la segunda etapa ($t_1$).
Dado que el movimiento se define seg n la aceleraci n experimentada, la velocidad alcanzada al final de la primera etapa debe coincidir con la velocidad inicial de la segunda etapa ($v_1$).
En el caso de una aceleraci n constante, en la primera etapa, el posición final primera e inició segunda etapa ($s_1$) depende de la posición inicial ($s_0$), la velocidad inicial ($v_0$), la aceleración durante la primera etapa ($a_1$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo inicial ($t_0$), seg n:
En la segunda etapa, la posición final segunda etapa ($s_2$) depende de el posición final primera e inició segunda etapa ($s_1$), la velocidad primera etapa ($v_1$), la aceleración durante la segunda etapa ($a_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), seg n:
que se representa como:
Si el movimiento consiste en dos etapas con diferentes aceleraciones constantes $a_1$ y $a_2$:
• Comienza en un tiempo $t_0$ en una posici n $s_0$ y velocidad $v_0$.
• Termina el movimiento en un tiempo $t_2$ en una posici n $s_2$ y velocidad $v_2$.
La clave reside en el proceso de transici n de una etapa a otra:
• Las velocidades var an seg n las aceleraciones pero son iguales en el punto de transici n entre etapas ($v_1$).
• Las posiciones var an seg n la velocidad pero son iguales en el punto de transici n entre etapas ($s_1$).
• Los tiempos son iguales en el punto de transici n entre etapas ($t_1$).
Esto se resume en las siguientes gr ficas:
Las ecuaciones que cumplen estas relaciones dan origen al siguiente modelo que permite calcular cualquier escenario:
La aceleraci n se define como la variaci n de la velocidad por unidad de tiempo.
Por lo tanto, es necesario establecer la diferencia de velocidad ($\Delta v$) en funci n de la velocidad ($v$) y la velocidad inicial ($v_0$) de la siguiente manera:
La aceleraci n se define como la variaci n de la velocidad por unidad de tiempo.
Por lo tanto, es necesario establecer la diferencia de velocidad ($\Delta v$) en funci n de la velocidad ($v$) y la velocidad inicial ($v_0$) de la siguiente manera:
Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duraci n se determina restando el tiempo inicial al tiempo final:
Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duraci n se determina restando el tiempo inicial al tiempo final:
La proporci n en la que la variaci n de la velocidad a lo largo del tiempo se define como la aceleración media ($\bar{a}$). Para medirla, es necesario observar la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$).
Un m todo com n para medir la aceleraci n media consiste en utilizar una l mpara estrobosc pica que ilumina el objeto en intervalos definidos. Al tomar una fotograf a, se puede determinar la distancia recorrida por el objeto en ese tiempo. Al calcular dos velocidades consecutivas, se puede determinar su variaci n y, con el tiempo transcurrido entre las fotos, la aceleraci n media.
La ecuaci n que describe la aceleraci n media es la siguiente:
Es importante tener en cuenta que la aceleraci n media es una estimaci n de la aceleraci n real.
El problema principal radica en que si la aceleraci n var a durante el tiempo transcurrido, el valor de la aceleraci n media puede diferir en gran medida de la aceleraci n promedio
.
Por lo tanto, la clave es
Determinar la aceleraci n en un per odo de tiempo suficientemente corto para minimizar la variaci n.
La proporci n en la que la variaci n de la velocidad a lo largo del tiempo se define como la aceleración media ($\bar{a}$). Para medirla, es necesario observar la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$).
Un m todo com n para medir la aceleraci n media consiste en utilizar una l mpara estrobosc pica que ilumina el objeto en intervalos definidos. Al tomar una fotograf a, se puede determinar la distancia recorrida por el objeto en ese tiempo. Al calcular dos velocidades consecutivas, se puede determinar su variaci n y, con el tiempo transcurrido entre las fotos, la aceleraci n media.
La ecuaci n que describe la aceleraci n media es la siguiente:
Es importante tener en cuenta que la aceleraci n media es una estimaci n de la aceleraci n real.
El problema principal radica en que si la aceleraci n var a durante el tiempo transcurrido, el valor de la aceleraci n media puede diferir en gran medida de la aceleraci n promedio
.
Por lo tanto, la clave es
Determinar la aceleraci n en un per odo de tiempo suficientemente corto para minimizar la variaci n.
Si la aceleración constante ($a_0$), entonces la aceleración media ($\bar{a}$) es igual al valor de la aceleraci n, es decir,
En este caso, la velocidad ($v$) como funci n de el tiempo ($t$) se puede calcular recordando que est asociada con la diferencia entre la velocidad ($v$) y la velocidad inicial ($v_0$), as como el tiempo ($t$) y el tiempo inicial ($t_0$).
De esta manera, la ecuaci n representa una l nea recta en el espacio de velocidad-tiempo.
Si la aceleración constante ($a_0$), entonces la aceleración media ($\bar{a}$) es igual al valor de la aceleraci n, es decir,
En este caso, la velocidad ($v$) como funci n de el tiempo ($t$) se puede calcular recordando que est asociada con la diferencia entre la velocidad ($v$) y la velocidad inicial ($v_0$), as como el tiempo ($t$) y el tiempo inicial ($t_0$).
De esta manera, la ecuaci n representa una l nea recta en el espacio de velocidad-tiempo.
En el caso de que una aceleración constante ($a_0$), la variable la velocidad ($v$) var a de forma lineal con respecto a el tiempo ($t$), utilizando la velocidad inicial ($v_0$) y el tiempo inicial ($t_0$):
As , el rea bajo esta recta se puede calcular, lo que nos proporciona la distancia recorrida en un tiempo ($\Delta s$). Al combinar esto con la posición inicial ($s_0$), podemos calcular la posición ($s$), lo que resulta en:
Esto corresponde a la forma general de una par bola.
En el caso de que una aceleración constante ($a_0$), la variable la velocidad ($v$) var a de forma lineal con respecto a el tiempo ($t$), utilizando la velocidad inicial ($v_0$) y el tiempo inicial ($t_0$):
As , el rea bajo esta recta se puede calcular, lo que nos proporciona la distancia recorrida en un tiempo ($\Delta s$). Al combinar esto con la posición inicial ($s_0$), podemos calcular la posición ($s$), lo que resulta en:
Esto corresponde a la forma general de una par bola.
En el caso de una aceleraci n constante, podemos calcular la posición ($s$) a partir de la posición inicial ($s_0$), la velocidad inicial ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) seg n la ecuaci n:
Esto nos permite calcular la relaci n entre la distancia de aceleraci n/frenado y el cambio de velocidad:
En el caso de una aceleraci n constante, podemos calcular la posición ($s$) a partir de la posición inicial ($s_0$), la velocidad inicial ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) seg n la ecuaci n:
Esto nos permite calcular la relaci n entre la distancia de aceleraci n/frenado y el cambio de velocidad:
Podemos calcular la distancia recorrida en un tiempo ($\Delta s$) a partir de la posición inicial ($s_0$) y la posición ($s$) mediante la siguiente ecuaci n:
Podemos calcular la distancia recorrida en un tiempo ($\Delta s$) a partir de la posición inicial ($s_0$) y la posición ($s$) mediante la siguiente ecuaci n:
ID:(1435, 0)
