Utilisateur:
Le décollage
Storyboard 
La clé pour décoller est de modifier l'aile de manière à obtenir une portance suffisante à des vitesses plus basses, ce qui permet un décollage réussi sur une longueur de piste donnée.
ID:(1464, 0)
Coefficient de portance
Description
Le coefficient de portance est une fonction de l'angle d\'attaque et suit généralement la tendance indiquée dans la figure suivante :
Dans le cas illustré, la pente est d\'environ 1,5 pour 15 degrés, ce qui correspond à 0,1 1/degré ou 5,73 1/radian.
ID:(7148, 0)
Variation du coefficient de portance
Description
Les avions et les oiseaux sont capables de modifier la forme de leurs ailes. Les avions utilisent des volets (flaps), tandis que les oiseaux ajustent la position de leurs plumes primaires et secondaires. Ainsi, ils parviennent à obtenir un coefficient de portance élevé à basse vitesse lors du décollage et de l\'atterrissage, et un coefficient de portance réduit à haute vitesse.
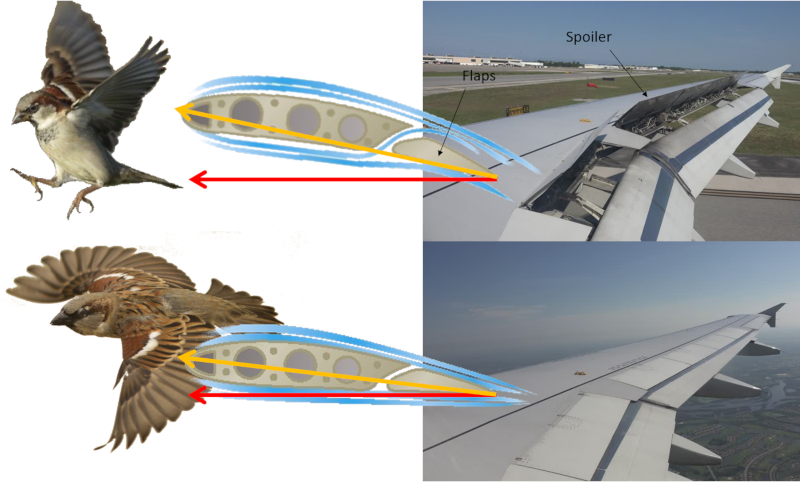
De plus, les avions sont également équipés de spoilers qui aident à freiner lors de l\'atterrissage.
ID:(11072, 0)
Le décollage
Modèle
La clé pour décoller est de modifier l'aile de manière à obtenir une portance suffisante à des vitesses plus basses, ce qui permet un décollage réussi sur une longueur de piste donnée.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
A force de levage ($F_L$), en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$), se trouve dans
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Si nous consid rons a surface génératrice de portance ($S_w$), d fini par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
et pour le coefficient de portance ($C_L$), d fini comme
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
nous obtenons
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
(ID 4417)
(ID 4441)
A force de levage ($F_L$) avec a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$) et a vitesse par rapport au milieu ($v$) est repr sent par
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ce qui, avec a masse corporelle ($m$) et a accélération gravitationnelle ($g$), doit tre gal :
| $ F_g = m g $ |
c'est- -dire :
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
ce qui donne :
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
(ID 4442)
Le coefficient de portance ($C_L$) est calcul avec a masse corporelle ($m$), a accélération gravitationnelle ($g$), a surface génératrice de portance ($S_w$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) comme suit :
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Ainsi, avec a constante de proportionnalité du coefficient de portance ($c$) et le accélération maximale ($\alpha$),
| $ C_L = c \alpha $ |
nous obtenons
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
(ID 4443)
Si nous galons a force de propulsion ($F_p$) avec a force de résistance ($F_W$) avec le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) dans
nous obtenons, pour un a vitesse maximum ($v_p$),
$F_p = \displaystyle\frac{1}{2} \rho S_w C_L v_p ^2$
ce qui, lorsqu'on le r sout pour la vitesse maximale, donne
(ID 14507)
A vitesse par rapport au milieu ($v$) pour un avion qui d colle satisfait l' quation avec a accélération maximale ($a_p$), a vitesse maximum ($v_p$) et le heure de décollage ($t$) :
| $\displaystyle\frac{dv}{dt}=a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
En int grant, nous obtenons l'expression suivante :
$\log(v_p + v) - \log(v_p - v) - \log(v_p + v_0) + \log(v_p - v_0)= \displaystyle\frac{2 a_p}{v_p} t$
Si a vitesse par rapport au milieu ($v$) est bien plus petit que a vitesse maximum ($v_p$), les logarithmes peuvent tre d velopp s en une s rie de Taylor, ce qui conduit une approximation du premier ordre :
| $ v = v_0 + a_p t $ |
(ID 14508)
Puisque la vitesse en fonction du temps est donn e par
| $ v = v_0 + a_p t $ |
nous pouvons exprimer la vitesse comme le taux de changement de la distance par rapport au temps :
$\displaystyle\frac{ds}{dt} = \sqrt{2 a_p v_p t }$
Cette quation peut tre int gr e, ce qui nous donne la relation entre la distance parcourue et le temps :
| $ l = v_0 t + \displaystyle\frac{1}{2} a_p t ^2$ |
(ID 14509)
(ID 14515)
Exemples
(ID 15173)
Le coefficient de portance est une fonction de l'angle d\'attaque et suit g n ralement la tendance indiqu e dans la figure suivante :
Dans le cas illustr , la pente est d\'environ 1,5 pour 15 degr s, ce qui correspond 0,1 1/degr ou 5,73 1/radian.
(ID 7148)
Les avions et les oiseaux sont capables de modifier la forme de leurs ailes. Les avions utilisent des volets (flaps), tandis que les oiseaux ajustent la position de leurs plumes primaires et secondaires. Ainsi, ils parviennent obtenir un coefficient de portance lev basse vitesse lors du d collage et de l\'atterrissage, et un coefficient de portance r duit haute vitesse.
De plus, les avions sont galement quip s de spoilers qui aident freiner lors de l\'atterrissage.
(ID 11072)
(ID 15186)
ID:(1464, 0)