mechanisms

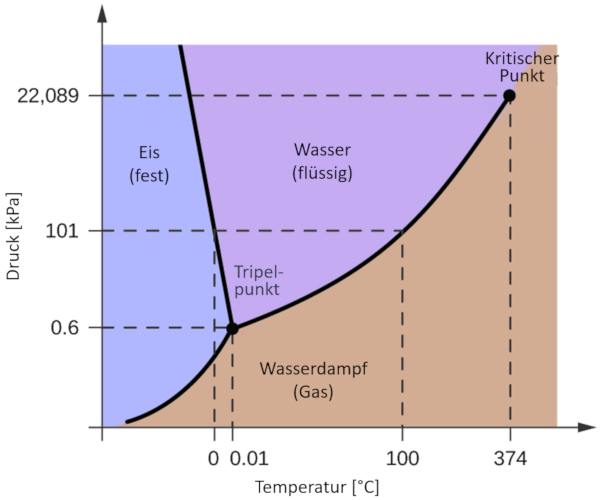
Eines der relevantesten Phasendiagramme f r unseren Planeten ist das des Wassers. Dieses Diagramm zeigt die drei klassischen Phasen: fest, fl ssig und gasf rmig, sowie verschiedene Phasen mit unterschiedlichen kristallinen Strukturen des Eises.

image

Der bedeutende Unterschied zu anderen Materialien besteht darin, dass im Druckbereich von 611 Pa bis 209,9 MPa die feste Phase ein gr eres Volumen einnimmt als die fl ssige Phase. Diese Eigenschaft spiegelt sich im Phasendiagramm als eine negative Neigung entlang der Grenzlinie zwischen der festen Phase (hexagonales Eis) und der fl ssigen Phase (Wasser) wider.

Wenn der Differential der Gibbs Freien Energie ($dG$) konstant ist, bedeutet dies, dass f r die Pressure Variation ($dp$) und die Temperaturschwankungen ($dT$), die Werte von die Entropie ($S$) und der Volumen ($V$) in Phase 1

$dG = -S_1dT+V_1dp$

und die Entropie ($S$) und der Volumen ($V$) in Phase 2

$dG = -S_2dT+V_2dp$

ergeben

$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$

Die Ver nderung in die Entropie ($S$) zwischen beiden Phasen entspricht der Latentwärme ($L$) geteilt durch die Absolute Temperatur ($T$):

$S_2 - S_1 =\displaystyle\frac{ L }{ T }$

Dann, mit der Definition von die Volumenvariation beim Phasenwechsel ($\Delta V$)

$\Delta V \equiv V_2 - V_1$

erhalten wir die Clausius-Clapeyron-Gleichung [1,2,3]

equation=12824

[1] " ber die Art der Bewegung, welche wir W rme nennen", Rudolf Clausius, Annalen der Physik und Chemie, 155(6), 368-397. (1850)

[2] " ber eine ver nderte Form des zweiten Hauptsatzes der mechanischen W rmetheorie", Rudolf Clausius, Annalen der Physik, 176(3), 353-400. (1857)

[3] "M moire sur la puissance motrice de la chaleur" (Denkschrift ber die bewegende Kraft der W rme), Beno t Paul mile Clapeyron, Journal de l' cole Royale Polytechnique, 14, 153-190. (1834)

Mit dem Clausius-Clapeyron-Gesetz, das von die Pressure Variation ($dp$), die Temperaturschwankungen ($dT$), der Latentwärme ($L$), die Volumenvariation beim Phasenwechsel ($\Delta V$) und die Absolute Temperatur ($T$) abh ngt und wie folgt ausgedr ckt wird:

equation=12824

und der Definition von der Molare Latenzwärme ($l_m$), bei der der Latentwärme ($L$) wie folgt mit die Molmasse ($M_m$) zusammenh ngt:

equation=9273

und der Variation des Molvolumens während des Phasenwechsels ($\Delta v_m$), bei der die Volumenvariation beim Phasenwechsel ($\Delta V$) wie folgt mit die Molmasse ($M_m$) zusammenh ngt:

equation=12823

erhalten wir:

equation=12822

Eines der Ph nomene, zu denen auch die Thermodynamik geh rt, ist die Untersuchung von Zustands nderungen. Es gibt drei Grundzust nde: Gas, Fl ssigkeit und Feststoff.

Bei Gas bewegen sich die Partikel nahezu frei und interagieren nur mit sporadischen St en.

Im Falle einer Fl ssigkeit ist die Wechselwirkung dauerhaft. Trotzdem k nnen die Partikel ohne dauerhafte Verbindungen zu den Nachbarn verschoben werden.

Im Fall des Feststoffs sind die Wechselwirkungen so, dass die Partikel nicht mehr verschoben werden k nnen und nur um einen Gleichgewichtspunkt schwingen, der durch die benachbarten Partikel definiert wird.

Die Untersuchung der Zustands nderungen versucht zu erkl ren, warum das Material in einer Form in die andere bergeht und umgekehrt. In der Medizin sind diese Ver nderungen f r Prozesse relevant, bei denen beispielsweise Substanzen verdampfen oder sich aufl sen. Dies sowohl zur Entfernung von Materialien als auch zur Temperaturreduzierung wie Schwei .

Wasser ist ein Sonderfall, da sein Phasendiagramm einen wesentlichen Unterschied in Bezug auf die berwiegende Mehrheit der Materialien darstellt: Die Linie, die die feste und die fl ssige Phase trennt, weist eine negative Steigung auf.

Dies liegt an der Tatsache, dass der Wasserwechsel von fest zu fl ssig sein Volumen verringert und damit die Variation des Volumens $ \ Delta V $ negativ ist und die Steigung in der Clausius-Clapeyron-Gleichung negativ wird.

Diese Eigenschaft von Wasser f hrt dazu, dass, wenn die Temperatur in fl ssigem Zustand $ (dT , negativ) $ beim Erreichen des Phasenwechsels gesenkt wird, der Druck $ (dp) $ ansteigt, w hrend er in einer normalen Fl ssigkeit verringert wird . Dies f hrt beispielsweise im Winter dazu

Das Einfrieren des Wassers, das sich in den Rissen und Rissen der Felsen in den Bergen angesammelt hat, erzeugt Druck, der zu seinem Bruch und letztendlich zur Erosion unserer Geographie f hrt.

Wenn die Oberfl che eines Sees gefroren ist, kapselt sich das Wasser des Sees ein und verhindert, dass es sich ausdehnt und Eis bildet. Dies verhindert, dass die Seen zu Boden gefrieren, w hrend das Leben im Inneren erhalten bleibt.

Rudolf Clausius (1822-1888) war ein deutscher Physiker und Mathematiker, der bedeutende Beitr ge auf dem Gebiet der Thermodynamik geleistet hat. Er ist am besten bekannt f r die Formulierung des zweiten Hauptsatzes der Thermodynamik und die Einf hrung des Konzepts der Entropie als grundlegende Gr e im Studium von Energie bertragung und -umwandlung in physikalischen Systemen.

image

model

Die Evaporated Messe ($\Delta m$) wird unter Verwendung von der Latentwärme ($L$) und der Phasenwechsel Wärme ($\Delta Q$) wie folgt definiert:

kyon

Das Clausius-Clapeyron-Gesetz stellt einen Zusammenhang zwischen die Pressure Variation ($dp$) und die Temperaturschwankungen ($dT$) mit der Latentwärme ($L$), die Absolute Temperatur ($T$) und ERROR:5239 < her /var> wie folgt:

kyon

In vielen F llen steht nicht die latente molare W rme zur Verf gung, sondern die latente W rme, die beispielsweise in Joule pro Kilogramm (J / kg) ausgedr ckt wird. Da die Dampfdruckgleichung mit der latenten molaren W rme funktioniert, m ssen wir die latente W rme in latente molare W rme umwandeln. Da letzteres pro Mol ist, reicht es aus, die latente W rme L durch die Molmasse M_m zu teilen, um die latente molare W rme zu erhalten

kyon

Im Fall von Wasser liegt die latente Verdampfungsw rme in der Gr enordnung von L\sim 2,256\times 10^6J/kg, w hrend die Molmasse M_m\ sim 18,g/cm^ 3 = 0,018,kg/m^3 betr gt, was zu einer latenten molaren W rme von L_m\sim 40600,J/mol = 40,6,kJ/mol f hrt.

Die nderung des Volumens zwischen dem Material in zwei verschiedenen Zust nden kann in Mol ausgedr ckt werden

kyon

um einen charakteristischen Indikator f r das Material zu erhalten.

Die Clausius-Clapeyron-Gleichung stellt einen Zusammenhang zwischen die Pressure Variation ($dp$) und die Temperaturschwankungen ($dT$) mit die Absolute Temperatur ($T$), der Molare Latenzwärme ($l_m$) und ERROR:9868 < her /var> wie folgt:

kyon