Calorimetría
Storyboard 
La calorimetría es el proceso de medir el calor asociado con un cambio en una variable de estado. Estas variables de estado incluyen típicamente la temperatura, la presión y el volumen, aunque pueden incluirse otras dependiendo del estado que se esté describiendo.
Cuando se mide cómo varía la temperatura en relación con el calor suministrado o extraído, se habla de capacidad calórica. En el caso de un gas, la capacidad calórica está influenciada por las demás variables de estado. Por lo tanto, se define y mide la capacidad calórica a volumen constante o a presión constante.
ID:(789, 0)
Mecanismos
Definición 
La calorimetría es la ciencia de medir la cantidad de calor involucrado en reacciones químicas, cambios físicos o capacidad calorífica. Cuantifica el calor intercambiado en los procesos, proporcionando datos esenciales sobre los cambios de energía involucrados. La calorimetría determina la capacidad calorífica de las sustancias, indicando cómo responden los diferentes materiales al calor. También mide los cambios de entalpía en las reacciones químicas, mostrando si son exotérmicas o endotérmicas. Además, la calorimetría estudia las transiciones de fase como la fusión, la ebullición o la sublimación al medir el calor absorbido o liberado. Los datos obtenidos de la calorimetría pueden usarse para derivar otras propiedades termodinámicas como la entropía y la energía libre de Gibbs, ofreciendo una comprensión completa del comportamiento de un sistema. El principio fundamental implica el uso de un calorímetro para medir con precisión el intercambio de calor mediante el monitoreo de los cambios de temperatura, lo cual es crucial en campos como la química, la física, la biología y la ingeniería.
ID:(15244, 0)
Convertidor de trabajo en calor
Imagen 
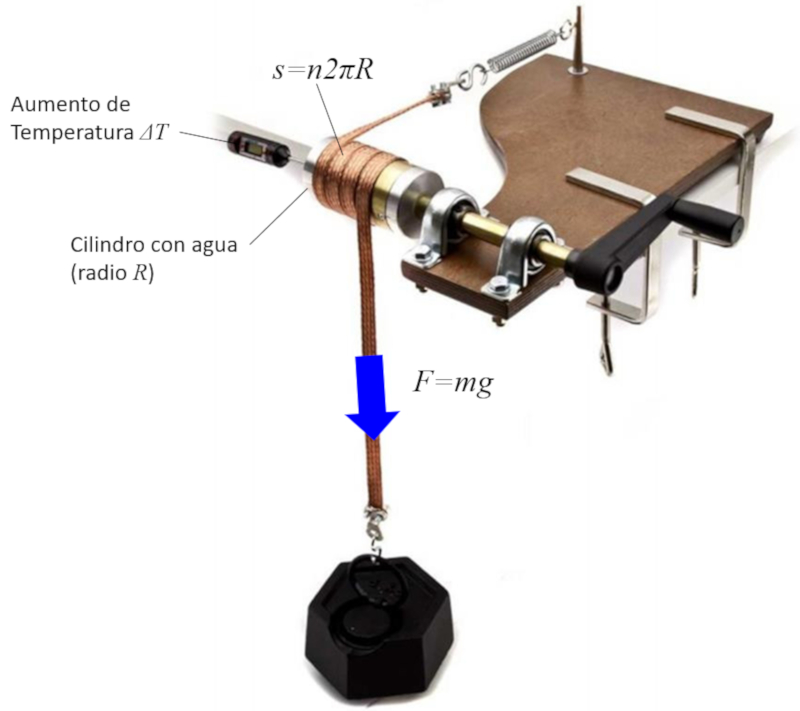
La conversión de trabajo en energía se estudia mediante la generación de calor a través del rozamiento. Para este fin, se coloca una banda metálica alrededor de un cilindro que contiene agua y un termómetro. Al girar la manivela, el rozamiento genera calor, lo que resulta en el calentamiento del agua. Si se mide la fuerza aplicada, el número de vueltas realizadas y el radio del cilindro, es posible estimar la distancia recorrida, lo que permite estimar la energía como el producto de la fuerza por la distancia.
ID:(1884, 0)
Contenido calórico de un solido y liquido
Nota 
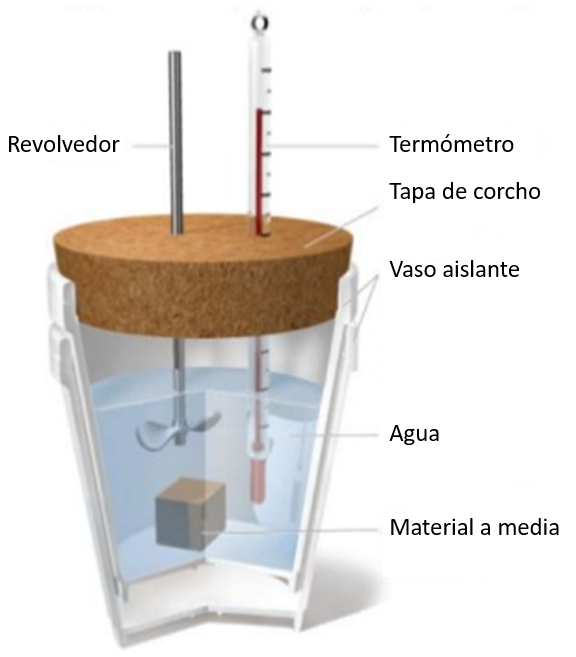
Si se tiene una muestra a una temperatura dada y se sumerge en un vaso de agua a una temperatura menor, se observará un incremento de la temperatura del agua. Este incremento dependerá de la capacidad calorífica específica y la masa de la muestra:
la calor suministrado al liquido o solido ($\Delta Q$) está relacionado con la variación de la temperatura ($\Delta T$) y la capacidad calórica ($C$) de la siguiente manera:
| $ \Delta Q = C \Delta T $ |
Donde la capacidad calórica ($C$) se puede reemplazar por el calor específico ($c$) y la masa ($M$) utilizando la siguiente relación:
| $ c =\displaystyle\frac{ C }{ M }$ |
Por lo tanto, se obtiene:
| $ \Delta Q = M c \Delta T$ |
ID:(15809, 0)
Calentamiento bajo volumen constante
Cita 
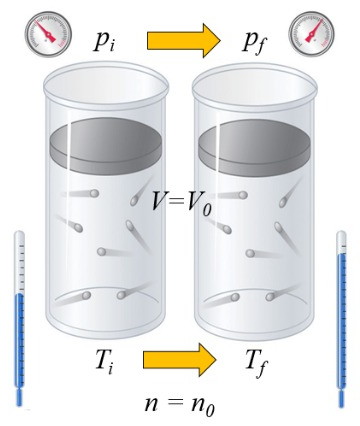
Si se calienta un gas, la capacidad calorífica depende de la forma en que esto ocurre. Una forma es a volumen constante, es decir, se mantiene el volumen fijo y se permite que el sistema sea expuesto a una presión mayor o menor:
la capacidad calórica ($C$) en sólidos y líquidos puede considerarse como una constante $C$ que relaciona la variación de la calor suministrado al liquido o solido ($\Delta Q$) y la variación de Temperature ($\Delta T$) mediante la ecuación:
| $ \Delta Q = C \Delta T $ |
En el caso de que el volumen ($V$) sea constante, la variación del volumen ($\Delta V$) es nulo:
$dV = 0$
y en tal caso, la variación de la energía interna ($dU$) es igual a el diferencial inexacto del calor ($\delta Q$):
$dU = \delta Q$
En el caso de un gas, el estado depende de la temperatura absoluta ($T$), la presión ($p$) y el volumen ($V$). Por lo tanto, si se agrega calor, el aumento de temperatura dependerá de si se mantiene constante el volumen o la presión. En el primer caso, se habla de la capacidad calórica a volumen constante ($C_V$) y se denota como $C_V$, y la relación es la siguiente:
| $ dU = C_V \Delta T $ |
Donde la capacidad calórica a volumen constante ($C_V$) puede ser reemplazado por el calor específico de gases a volumen constante ($c_V$) y la masa ($M$) utilizando la siguiente relación:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Por lo tanto, obtenemos:
| $ dU = c_V M \Delta T $ |
ID:(11190, 0)
Calentamiento bajo presión constante
Ejercicio 
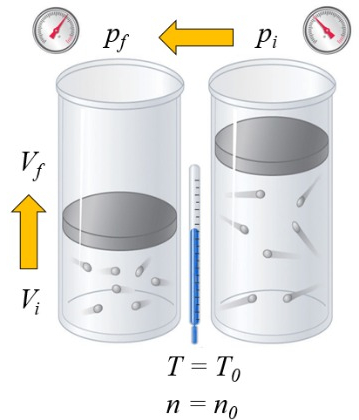
Si se calienta un gas, la capacidad calorífica depende de la forma en que esto ocurre. Una forma es a presión constante, es decir, se permite que el volumen se expanda o contraiga de modo que la presión se mantenga constante:
la capacidad calórica ($C$) en sólidos y líquidos puede considerarse como una constante $C$ que relaciona la variación de la variación del calor ($\Delta Q$) y la variación de Temperature ($\Delta T$) mediante la ecuación:
| $ \Delta Q = C \Delta T $ |
En el caso de un gas, el estado depende de la temperatura absoluta ($T$), la presión ($p$) y el volumen ($V$). Por lo tanto, si se agrega calor, el aumento de temperatura dependerá de si se mantiene constante el volumen o la presión. En el primer caso, se habla de la capacidad calórica a presión constante ($C_p$) y se denota como $C_p$, y la relación es la siguiente:
| $ \Delta Q = C_p \Delta T $ |
Donde la capacidad calórica a presión constante ($C_p$) puede ser reemplazado por el calor especifico a presión constante ($c_p$) y la masa ($M$) utilizando la siguiente relación:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Por lo tanto, obtenemos:
| $ \Delta Q = c_p M \Delta T $ |
ID:(11189, 0)
Calorimetría en gases
Descripción 
La calorimetría es el proceso de medir el calor asociado con un cambio en una variable de estado. Estas variables de estado incluyen típicamente la temperatura, la presión y el volumen, aunque pueden incluirse otras dependiendo del estado que se esté describiendo. Cuando se mide cómo varía la temperatura en relación con el calor suministrado o extraído, se habla de capacidad calórica. En el caso de un gas, la capacidad calórica está influenciada por las demás variables de estado. Por lo tanto, se define y mide la capacidad calórica a volumen constante o a presión constante.
Variables
Cálculos
Cálculos
Ecuaciones
La capacidad calórica ($C$) en s lidos y l quidos puede considerarse como una constante $C$ que relaciona la variaci n de la calor suministrado al liquido o solido ($\Delta Q$) y la variación de Temperature ($\Delta T$) mediante la ecuaci n:
| $ \Delta Q = C \Delta T $ |
En el caso de que el volumen ($V$) sea constante, la variación del volumen ($\Delta V$) es nulo:
$dV = 0$
y en tal caso, la variación de la energía interna ($dU$) es igual a el diferencial inexacto del calor ($\delta Q$):
$dU = \delta Q$
En el caso de un gas, el estado depende de la temperatura absoluta ($T$), la presión ($p$) y el volumen ($V$). Por lo tanto, si se agrega calor, el aumento de temperatura depender de si se mantiene constante el volumen o la presi n. En el primer caso, se habla de la capacidad calórica a volumen constante ($C_V$) y se denota como $C_V$, y la relaci n es la siguiente:
| $ dU = C_V \Delta T $ |
(ID 4862)
La capacidad calórica ($C$) en s lidos y l quidos puede considerarse como una constante $C$ que relaciona la variaci n de la variación del calor ($\Delta Q$) y la variación de Temperature ($\Delta T$) mediante la ecuaci n:
| $ \Delta Q = C \Delta T $ |
En el caso de un gas, el estado depende de la temperatura absoluta ($T$), la presión ($p$) y el volumen ($V$). Por lo tanto, si se agrega calor, el aumento de temperatura depender de si se mantiene constante el volumen o la presi n. En el primer caso, se habla de la capacidad calórica a presión constante ($C_p$) y se denota como $C_p$, y la relaci n es la siguiente:
| $ \Delta Q = C_p \Delta T $ |
(ID 4863)
Siguiendo una analog a al ERROR:5219,0 de l quidos y s lidos con la capacidad calórica ($C$) y la masa ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
existe tambi n un calor específico de gases a volumen constante ($c_V$) para calentamiento bajo volumen constante con la capacidad calórica a volumen constante ($C_V$):
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
(ID 11113)
Siguiendo una analog a al ERROR:5219,0 de l quidos y s lidos con la capacidad calórica ($C$) y la masa ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
existe tambi n un calor especifico a presión constante ($c_p$) para calentamiento bajo presi n constante con la capacidad calórica a presión constante ($C_p$):
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
(ID 11114)
La variación de la energía interna ($dU$) en relaci n con la variación de la temperatura ($\Delta T$) y la capacidad calórica a volumen constante ($C_V$) se expresa como:
| $ dU = C_V \Delta T $ |
Donde la capacidad calórica a volumen constante ($C_V$) puede ser reemplazado por el calor específico de gases a volumen constante ($c_V$) y la masa ($M$) utilizando la siguiente relaci n:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Por lo tanto, obtenemos:
| $ dU = c_V M \Delta T $ |
(ID 11115)
La calor suministrado al liquido o solido ($\Delta Q$) en relaci n con la variación de la temperatura ($\Delta T$) y la capacidad calórica a presión constante ($C_p$) se expresa de la siguiente manera:
| $ \Delta Q = C_p \Delta T $ |
Donde la capacidad calórica a presión constante ($C_p$) puede ser reemplazado por el calor especifico a presión constante ($c_p$) y la masa ($M$) utilizando la siguiente relaci n:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Por lo tanto, obtenemos:
| $ \Delta Q = c_p M \Delta T $ |
(ID 11116)
Ejemplos
La calorimetr a es la ciencia de medir la cantidad de calor involucrado en reacciones qu micas, cambios f sicos o capacidad calor fica. Cuantifica el calor intercambiado en los procesos, proporcionando datos esenciales sobre los cambios de energ a involucrados. La calorimetr a determina la capacidad calor fica de las sustancias, indicando c mo responden los diferentes materiales al calor. Tambi n mide los cambios de entalp a en las reacciones qu micas, mostrando si son exot rmicas o endot rmicas. Adem s, la calorimetr a estudia las transiciones de fase como la fusi n, la ebullici n o la sublimaci n al medir el calor absorbido o liberado. Los datos obtenidos de la calorimetr a pueden usarse para derivar otras propiedades termodin micas como la entrop a y la energ a libre de Gibbs, ofreciendo una comprensi n completa del comportamiento de un sistema. El principio fundamental implica el uso de un calor metro para medir con precisi n el intercambio de calor mediante el monitoreo de los cambios de temperatura, lo cual es crucial en campos como la qu mica, la f sica, la biolog a y la ingenier a.
(ID 15244)
La conversi n de trabajo en energ a se estudia mediante la generaci n de calor a trav s del rozamiento. Para este fin, se coloca una banda met lica alrededor de un cilindro que contiene agua y un term metro. Al girar la manivela, el rozamiento genera calor, lo que resulta en el calentamiento del agua. Si se mide la fuerza aplicada, el n mero de vueltas realizadas y el radio del cilindro, es posible estimar la distancia recorrida, lo que permite estimar la energ a como el producto de la fuerza por la distancia.

(ID 1884)
Si se tiene una muestra a una temperatura dada y se sumerge en un vaso de agua a una temperatura menor, se observar un incremento de la temperatura del agua. Este incremento depender de la capacidad calor fica espec fica y la masa de la muestra:

la calor suministrado al liquido o solido ($\Delta Q$) est relacionado con la variación de la temperatura ($\Delta T$) y la capacidad calórica ($C$) de la siguiente manera:
| $ \Delta Q = C \Delta T $ |
Donde la capacidad calórica ($C$) se puede reemplazar por el calor específico ($c$) y la masa ($M$) utilizando la siguiente relaci n:
| $ c =\displaystyle\frac{ C }{ M }$ |
Por lo tanto, se obtiene:
| $ \Delta Q = M c \Delta T$ |
(ID 15809)
Si se calienta un gas, la capacidad calor fica depende de la forma en que esto ocurre. Una forma es a volumen constante, es decir, se mantiene el volumen fijo y se permite que el sistema sea expuesto a una presi n mayor o menor:

la capacidad calórica ($C$) en s lidos y l quidos puede considerarse como una constante $C$ que relaciona la variaci n de la calor suministrado al liquido o solido ($\Delta Q$) y la variación de Temperature ($\Delta T$) mediante la ecuaci n:
| $ \Delta Q = C \Delta T $ |
En el caso de que el volumen ($V$) sea constante, la variación del volumen ($\Delta V$) es nulo:
$dV = 0$
y en tal caso, la variación de la energía interna ($dU$) es igual a el diferencial inexacto del calor ($\delta Q$):
$dU = \delta Q$
En el caso de un gas, el estado depende de la temperatura absoluta ($T$), la presión ($p$) y el volumen ($V$). Por lo tanto, si se agrega calor, el aumento de temperatura depender de si se mantiene constante el volumen o la presi n. En el primer caso, se habla de la capacidad calórica a volumen constante ($C_V$) y se denota como $C_V$, y la relaci n es la siguiente:
| $ dU = C_V \Delta T $ |
Donde la capacidad calórica a volumen constante ($C_V$) puede ser reemplazado por el calor específico de gases a volumen constante ($c_V$) y la masa ($M$) utilizando la siguiente relaci n:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Por lo tanto, obtenemos:
| $ dU = c_V M \Delta T $ |
(ID 11190)
Si se calienta un gas, la capacidad calor fica depende de la forma en que esto ocurre. Una forma es a presi n constante, es decir, se permite que el volumen se expanda o contraiga de modo que la presi n se mantenga constante:

la capacidad calórica ($C$) en s lidos y l quidos puede considerarse como una constante $C$ que relaciona la variaci n de la variación del calor ($\Delta Q$) y la variación de Temperature ($\Delta T$) mediante la ecuaci n:
| $ \Delta Q = C \Delta T $ |
En el caso de un gas, el estado depende de la temperatura absoluta ($T$), la presión ($p$) y el volumen ($V$). Por lo tanto, si se agrega calor, el aumento de temperatura depender de si se mantiene constante el volumen o la presi n. En el primer caso, se habla de la capacidad calórica a presión constante ($C_p$) y se denota como $C_p$, y la relaci n es la siguiente:
| $ \Delta Q = C_p \Delta T $ |
Donde la capacidad calórica a presión constante ($C_p$) puede ser reemplazado por el calor especifico a presión constante ($c_p$) y la masa ($M$) utilizando la siguiente relaci n:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Por lo tanto, obtenemos:
| $ \Delta Q = c_p M \Delta T $ |
(ID 11189)
(ID 15303)
La variación de la energía interna ($dU$) es para el caso de que el volumen ($V$) es constante igual a la capacidad calórica a volumen constante ($C_V$) por la temperatura absoluta ($T$):
| $ dU = C_V \Delta T $ |
(ID 4862)
La variación del calor ($\Delta Q$) se puede calcular de la capacidad calórica a presión constante ($C_p$) y la variación de Temperature ($\Delta T$) mediante:
| $ \Delta Q = C_p \Delta T $ |
(ID 4863)
El calor específico de gases a volumen constante ($c_V$) es igual a la capacidad calórica a volumen constante ($C_V$) dividido por la masa ($M$):
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
(ID 11113)
La relaci n entre la variaci n de la variación de la energía interna ($dU$) y la variación de la temperatura ($\Delta T$) es con el calor específico de gases a volumen constante ($c_V$) y la masa ($M$) igual a:
| $ dU = c_V M \Delta T $ |
(ID 11115)
El calor especifico a presión constante ($c_p$) es igual a la capacidad calórica a presión constante ($C_p$) dividido por la masa ($M$):
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
(ID 11114)
La calor suministrado al liquido o solido ($\Delta Q$) se puede calcular con el calor especifico a presión constante ($c_p$), la masa ($M$) y la variación de la temperatura ($\Delta T$) mediante:
| $ \Delta Q = c_p M \Delta T $ |
(ID 11116)
ID:(789, 0)
