Usuario:
Condiciones de Ruptura
Definición 
Si el concreto se tensa cede primero en forma elástica hasta llegar a una tensión crítica en que comienza a deformarse en forma plástica. Gracias al reforzamiento con acero no colapsa a cero si no comienza a deformarse en forma macroscopica.
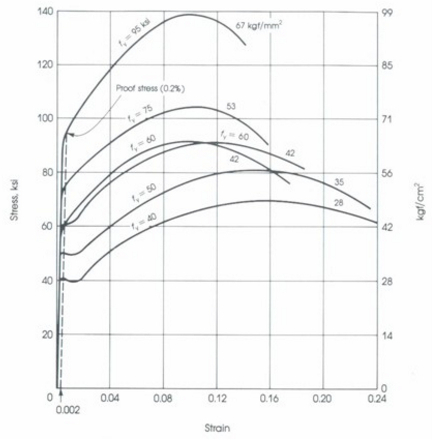
Las curvas llevan una etiqueta indicada en ksi que muestra la tensión en que comienza la deformación plástica. La unidad ksi se asocia a MPa según la siguiente tabla:
ksi | MPa
:--:|:----:
40 | 276
60 | 414
80 | 552
Por ello se puede definir una tensión critica $\sigma_c$ que no debemos superar.
ID:(157, 0)
Tensión en Viga apoyado - apoyado
Imagen
La tensión en una viga doblemente apoyado se puede calcular de la defromación
| $u(x)=\displaystyle\frac{qx}{24EI}(L^3-2Lx^2+x^3)$ |
con la ecuación
| $\sigma(x)=-zE\displaystyle\frac{d^2u}{dx^2}$ |
se obtiene en este caso que
| $\sigma(x)=-\displaystyle\frac{zqx(L-x)}{2I}$ |
ID:(162, 0)
Fracturas en Vigas
Storyboard
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
Si el concreto se tensa cede primero en forma el stica hasta llegar a una tensi n cr tica en que comienza a deformarse en forma pl stica. Gracias al reforzamiento con acero no colapsa a cero si no comienza a deformarse en forma macroscopica.
Las curvas llevan una etiqueta indicada en ksi que muestra la tensi n en que comienza la deformaci n pl stica. La unidad ksi se asocia a MPa seg n la siguiente tabla:
ksi | MPa
:--:|:----:
40 | 276
60 | 414
80 | 552
Por ello se puede definir una tensi n critica $\sigma_c$ que no debemos superar.
La tensi n en una viga doblemente empotrada se puede calcular de la defromaci n
con la ecuaci n
se obtiene en este caso que
Como tensi n en una viga doblemente empotrada es
que es m ximo en el centro $x=L/2$ y como el segundo momento de rea es
se el m ximo en la tensi n
que no debe superar la tensi n cr tica de ruptura por cizalla.
La tensi n en una viga empotrada y apoyada se puede calcular de la defromaci n
con la ecuaci n
se obtiene en este caso que
Como tensi n en una viga doblemente empotrada es
que es m ximo en el centro $x=L/2$ y como el segundo momento de rea es
se el m ximo en la tensi n
que no debe superar la tensi n cr tica de ruptura por cizalla.
La tensi n en una viga doblemente empotrada se puede calcular de la deformaci n
con la ecuaci n
se obtiene en este caso que
Como tensi n en una viga doblemente empotrada es
que es m ximo en el centro $x=L$ y como el segundo momento de rea es
se el m ximo en la tensi n
que no debe superar la tensi n cr tica de ruptura por cizalla.
La tensi n en una viga doblemente apoyado se puede calcular de la defromaci n
con la ecuaci n
se obtiene en este caso que
Como tensi n en una viga doblemente empotrada es
que es m ximo en el centro $x=L/2$ y como el segundo momento de rea es
se el m ximo en la tensi n
que no debe superar la tensi n cr tica de ruptura por cizalla.
ID:(1064, 0)