A ação da força de Coriolis
Storyboard 
Sempre que observamos um objeto se movendo em linha reta a uma velocidade constante a partir de um sistema em rotação (como a superfície da Terra), parece que ele está realizando um movimento curvo. Isso pode ser modelado introduzindo uma força fictícia chamada força de Coriolis. Com ela, podemos entender uma série de movimentos observados no oceano e na atmosfera.
ID:(1521, 0)
A ação da força de Coriolis
Storyboard 
Sempre que observamos um objeto se movendo em linha reta a uma velocidade constante a partir de um sistema em rotação (como a superfície da Terra), parece que ele está realizando um movimento curvo. Isso pode ser modelado introduzindo uma força fictícia chamada força de Coriolis. Com ela, podemos entender uma série de movimentos observados no oceano e na atmosfera.
Variáveis
Cálculos
Cálculos
Equações
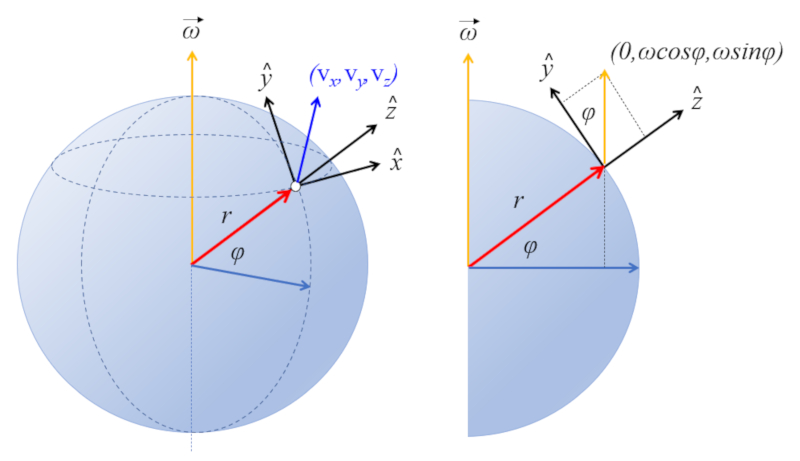
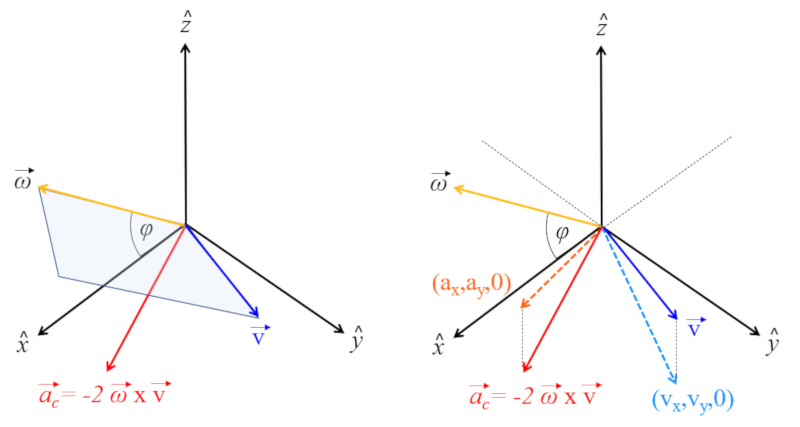
Na superf cie da Terra, o eixo aponta para o norte e forma um ngulo igual a la latitude ($\varphi$) em rela o ao plano. Portanto, la velocidade angular ($\vec{\omega}$) igual a:
$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$
E como la velocidade corporal ($\vec{v}$) :
$\vec{v}=(v_x,v_y,v_z)$
Assim, a defini o de la aceleração de Coriolis ($\vec{a}_c$):
resulta na componente x igual a:
Na superf cie da Terra, o eixo aponta para o norte e forma um ngulo igual a la latitude ($\varphi$) em rela o ao plano. Portanto, la velocidade angular ($\vec{\omega}$) igual a:
$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$
E como la velocidade corporal ($\vec{v}$) :
$\vec{v}=(v_x,v_y,v_z)$
Assim, a defini o de la aceleração de Coriolis ($\vec{a}_c$):
resulta na componente y igual a:
Na superf cie da Terra, o eixo aponta para o norte e forma um ngulo igual a la latitude ($\varphi$) em rela o ao plano. Portanto, la velocidade angular ($\vec{\omega}$) igual a:
$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$
E como la velocidade corporal ($\vec{v}$) :
$\vec{v}=(v_x,v_y,v_z)$
Assim, a defini o de la aceleração de Coriolis ($\vec{a}_c$):
resulta na componente z igual a:
Como la aceleração de Coriolis na direção x ($a_{c,x}$) composto por la velocidade angular do planeta ($\omega$), la latitude ($\varphi$), la y velocidade do objeto ($v_y$) e la z velocidade do objeto ($v_z$):
e a defini o de o fator de Coriolis ($f$) :
al m da restri o de movimento na superf cie, onde:
$v_z = 0$
resulta que la aceleração de Coriolis na direção x ($a_{c,x}$) :
Como la aceleração de Coriolis na direção y ($a_{c,y}$) composto por la velocidade angular do planeta ($\omega$), la x velocidade do objeto ($v_x$) e la latitude ($\varphi$):
e a defini o de o fator de Coriolis ($f$) :
al m da restri o de um movimento na superf cie onde:
$v_z = 0$
isso leva a que la aceleração de Coriolis na direção y ($a_{c,y}$) seja:
Como la aceleração de Coriolis na direção y ($a_{c,y}$) composto por la velocidade angular do planeta ($\omega$), la x velocidade do objeto ($v_x$) e la latitude ($\varphi$):
e a defini o de o segundo fator de Coriolis ($e$) :
al m da restri o de um movimento na superf cie onde:
$v_z = 0$
isso leva a que la aceleração de Coriolis na superfície, na direção z ($a_{c,z}$) seja:
Exemplos
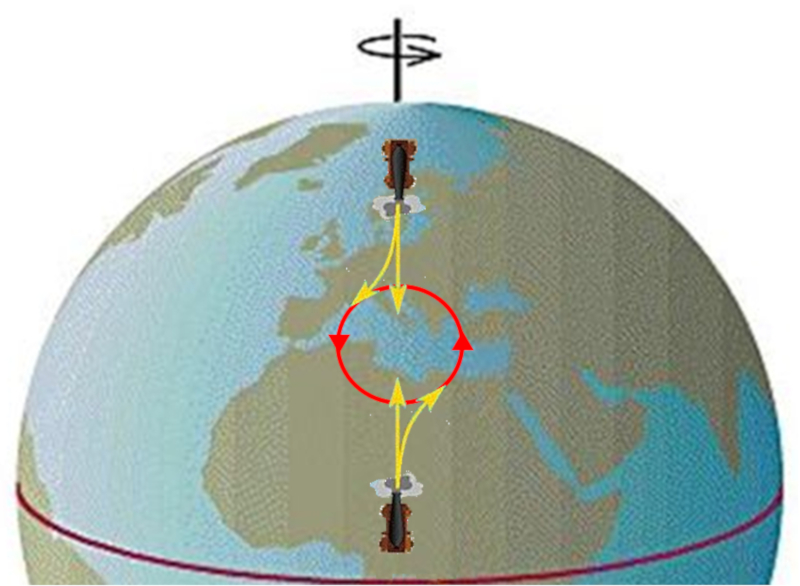
No v deo, observa-se como um objeto parece realizar um movimento curvo quando visto de um sistema em rota o. No entanto, a partir de um sistema n o rotativo, o movimento retil neo e com velocidade constante.
Para descrever o movimento de um corpo que se move em linha reta a partir de um sistema que gira, pode-se usar o artif cio de introduzir uma for a fict cia (que n o existe) que representa esse movimento. Essa for a fict cia conhecida como for a de Coriolis.
Estabelece-se um sistema de refer ncia local em que se define:
• o eixo z aponta para cima
• o eixo y aponta para o norte
• o eixo x aponta para leste
Com isso, o vetor da velocidade angular do planeta est no plano yz com um ngulo igual latitude do local:
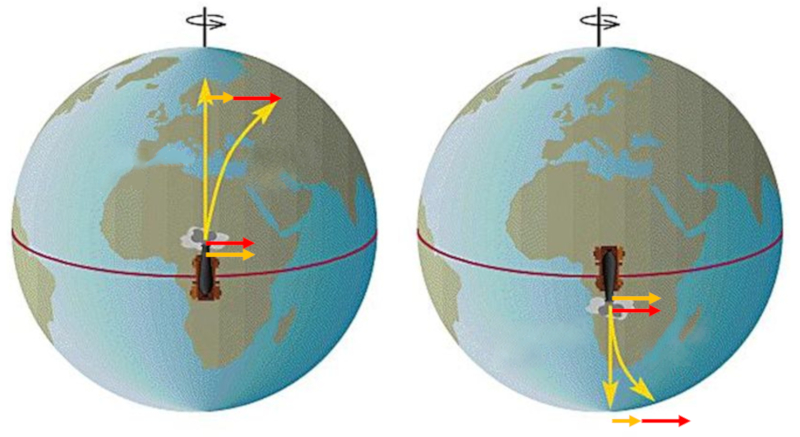
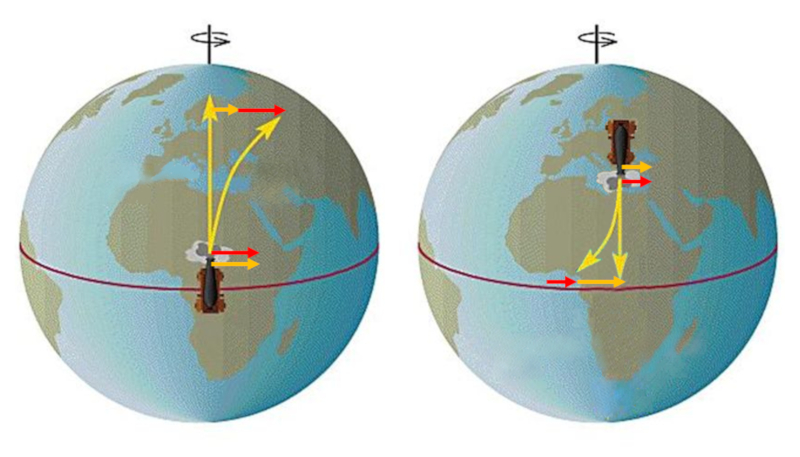
O efeito da aparente desvio pode ser observado especialmente na superf cie da Terra. Se um objeto for lan ado a partir do equador e avan ar para latitudes mais altas, parece "avan ar" simplesmente porque, em latitudes mais altas, a velocidade tangencial menor do que no equador.
Se um objeto for lan ado de um local distante do equador para o leste, observa-se que o corpo se desvia, ficando para tr s devido sua menor velocidade tangencial em compara o com latitudes mais pr ximas do equador.
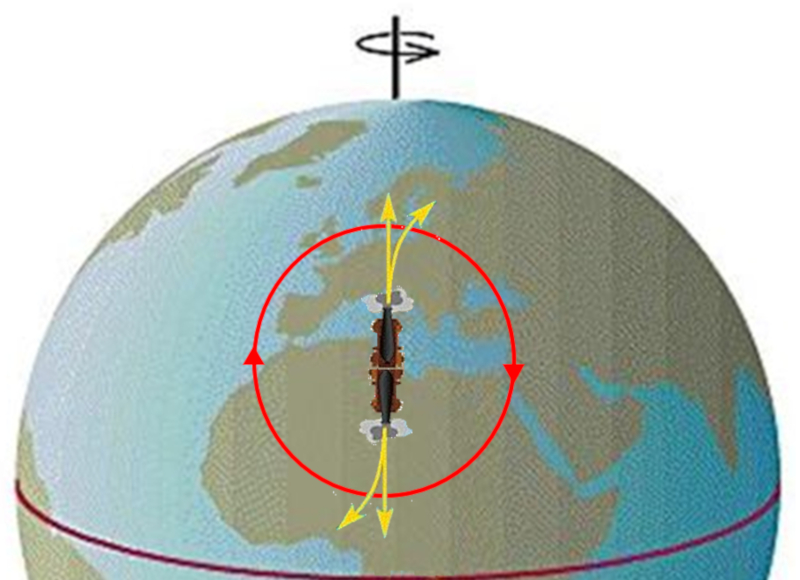
Se o meio em movimento flui de um ponto (por exemplo, no ar, de uma rea de alta press o), os fluxos s o atrasados ou adiantados dependendo se eles se dirigem para o equador ou para o polo. Isso leva forma o de um sistema que gira no sentido negativo (no hemisf rio norte), formando o que chamado de ciclone.
Se o meio que se desloca flui em dire o a um ponto (por exemplo, no ar, de uma baixa press o), os fluxos s o adiantados/atrasados, dependendo se v m do equador ou do polo. Isso leva forma o de um sistema que gira no sentido positivo (no hemisf rio norte), formando o que chamado de anticiclone.
Se apenas observarmos o que acontece no plano, veremos que sempre que nos movemos numa dire o espec fica, experimentamos uma acelera o perpendicular no sentido positivo. A magnitude dessa acelera o aumenta com a latitude, sendo zero no equador. Fora disso, proporcional velocidade angular, o que significa que, se o sistema de refer ncia n o estivesse girando, n o haveria um efeito de Coriolis.
A acelera o de Coriolis explica como um objeto se desvia de sua rota devido rota o do sistema de refer ncia.
importante entender que a 'for a', 'acelera o' ou 'efeito' de Coriolis um 'truque' matem tico para calcular como um corpo se comporta quando visto de um sistema que est girando. A equa o que melhor modela esse efeito la aceleração de Coriolis ($\vec{a}_c$) com la velocidade angular ($\vec{\omega}$) e la velocidade corporal ($\vec{v}$):
La aceleração de Coriolis ($\vec{a}_c$) com la velocidade angular ($\vec{\omega}$) e la velocidade corporal ($\vec{v}$):
Portanto, com la aceleração de Coriolis na direção x ($a_{c,x}$) junto com la velocidade angular do planeta ($\omega$), la y velocidade do objeto ($v_y$), la z velocidade do objeto ($v_z$) e la latitude ($\varphi$), a componente x .
La aceleração de Coriolis ($\vec{a}_c$) com la velocidade angular ($\vec{\omega}$) e la velocidade corporal ($\vec{v}$):
Ent o, com la aceleração de Coriolis na direção y ($a_{c,y}$) junto a la velocidade angular do planeta ($\omega$), la x velocidade do objeto ($v_x$) e la latitude ($\varphi$), a componente y :
La aceleração de Coriolis ($\vec{a}_c$) com la velocidade angular ($\vec{\omega}$) e la velocidade corporal ($\vec{v}$):
Ent o, com la aceleração de Coriolis na direção z ($a_{c,z}$) junto a la velocidade angular do planeta ($\omega$), la x velocidade do objeto ($v_x$) e la latitude ($\varphi$), a componente y :
Para simplificar as equa es, trabalhamos com um fator de Coriolis ($f$), que uma constante para o local f sico, pois inclui la velocidade angular do planeta ($\omega$) para a Terra e la latitude ($\varphi$) para o local:
No hemisf rio sul, a latitude negativa e, com ela, 8600, o que explica por que os sistemas giram na dire o oposta ao hemisf rio norte.
Para simplificar as equa es, trabalhamos com um segundo fator de Coriolis ($e$), que uma constante para o local f sico, pois inclui la velocidade angular do planeta ($\omega$) para a Terra e la latitude ($\varphi$) para o local:
Como la aceleração de Coriolis na direção x ($a_{c,x}$) pode ser reescrito com o fator de Coriolis ($f$) e a condi o de que n o h movimento vertical:
$v_z = 0$
ent o resulta que la aceleração de Coriolis na superfície, na direção x ($a_{c,x}$) :
Como la aceleração de Coriolis na direção x ($a_{c,x}$) pode ser reescrito com o fator de Coriolis ($f$) e sob a condi o de que n o haja movimento vertical:
$v_z = 0$
Assim, deduz-se que la aceleração de Coriolis na superfície, na direção y ($a_{c,y}$) :
Como la aceleração de Coriolis na direção z ($a_{c,z}$) pode ser reescrito com o segundo fator de Coriolis ($e$) e sob a condi o de que n o haja movimento vertical:
$v_z = 0$
Assim, deduz-se que la aceleração de Coriolis na superfície, na direção z ($a_{c,z}$) :
ID:(1521, 0)