Processus de diffusion
Modèle 
La diffusion se produit lorsquil existe une différence de concentration entre des régions, ce qui provoque le déplacement des particules des zones de forte concentration vers celles de plus faible concentration. Le flux résultant dépend de lampleur de cette différence et de la distance sur laquelle elle se manifeste. En analysant comment ce flux évolue entre deux points au fil du temps, on obtient une expression qui décrit lévolution locale de la concentration. Lorsque la vitesse de diffusion est constante, cette expression se simplifie et décrit une distribution en forme de cloche qui évolue avec le temps et la position. Cette distribution sélargit avec le temps, tandis que la hauteur de son maximum diminue proportionnellement.
Variables
Calculs
Calculs
Équations
A densité de flux ($j$) d pend de a constante de diffusion ($D$) et du gradient, lequel est estim partir de ERROR:9080 et a distance ($\Delta z$) :
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
Dans la limite o les intervalles discrets deviennent des diff rentiels infinit simaux ($\Delta z \rightarrow dz$), on obtient pour a concentration ($c$) et a position ($z$) :
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
(ID 12140)
ERROR:9080 varie avec a durée du temps ($\Delta t$) en fonction de a variation de la densité de flux ($\Delta j$), laquelle d pend son tour de a distance ($\Delta z$) :
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
Dans la limite o les intervalles discrets deviennent des diff rentiels infinit simaux ($\Delta z \rightarrow dz$, $\Delta t \rightarrow dt$), on obtient pour a concentration ($c$), a densité de flux ($j$), a position ($z$) et le temps ($t$) :
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
(ID 12144)
La deuxi me loi de Fick tablit que la variation de a concentration ($c$) par rapport le temps ($t$) est gale la variation de a densité de flux ($j$) par rapport a position ($z$) :
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
avec la relation pour a densité de flux ($j$) :
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
on obtient ainsi l quation de diffusion :
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
(ID 12145)
La deuxi me loi de Fick, qui relie a concentration ($c$), a constante de diffusion ($D$), a position ($z$) et le temps ($t$), sexprime comme suit :
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
Dans le cas o a constante de diffusion ($D$) est constante, cette quation se simplifie en :
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
(ID 12146)
L quation diff rentielle qui r git a concentration ($c$), dans le cas o a constante de diffusion ($D$) est constante, sexprime en fonction de a position ($z$) et le temps ($t$) :
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
dont la solution est :
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
(ID 12147)
Dans le cas d'une diffusion avec a constante de diffusion ($D$) constante, la distribution de a concentration ($c$) en fonction de a position ($z$) et le temps ($t$) prend la forme suivante :
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
En introduisant a écart type ($\sigma$) sous la forme :
| $ \sigma =\sqrt{2 D t }$ |
la distribution peut tre r crite comme suit :
| $ c =\displaystyle\frac{1}{\sqrt{2\pi} \sigma } e^{- z ^2/2 \sigma ^2 }$ |
(ID 16189)
A concentration ($c$) est influenc e par a vitesse du milieu ($u$), qui agit en opposition au processus de diffusion caract ris par a constante de diffusion ($D$) dans la r gion positive de a position ($z$), modifiant ainsi la distribution de le temps ($t$) selon :
| $\displaystyle\frac{\partial c}{\partial t} + u \displaystyle\frac{\partial c}{\partial z} = D \displaystyle\frac{\partial^2 c}{\partial z ^2}$ |
La solution de cette quation prend la forme suivante :
| $ c = c_0 [1 - erf\left(\displaystyle\frac{ z - u t }{ 2\sqrt{ D t }}\right)]$ |
(ID 16193)
Exemples
La diffusion r sulte de diff rences de concentration en particules. Autrement dit, lorsquil y a plus de particules dans une r gion que dans une autre, il est plus probable quelles se d placent de la r gion forte concentration vers celle faible concentration, plut t que linverse.

(ID 12139)
Dans un liquide ou un gaz, il peut exister des situations o la concentration dune certaine propri t (comme une substance, de la chaleur ou de la quantit de mouvement) nest pas homog ne.
Dans ce cas, les particules associ es cette propri t ont plus de chances de se d placer de la r gion forte concentration vers celle faible concentration, simplement parce quelles sont plus nombreuses dans la premi re. Le flux d pend donc la fois de la diff rence de concentration et de la distance sur laquelle elle se manifeste autrement dit, du gradient de concentration.
Si la concentration en un point $z$ dune solution est $c(z)$ et quen un autre point $z + \Delta z$ elle est $c(z + \Delta z)$, alors selon ERROR:9080 :
$\Delta c = c(z + \Delta z) - c(z)$
Ce qui d finit un gradient selon a distance ($\Delta z$) :
$\displaystyle\frac{c(z + \Delta z) - c(z)}{\Delta z} = \displaystyle\frac{\Delta c}{\Delta z} \sim \displaystyle\frac{\partial c}{\partial z}$
Dapr s a densité de flux ($j$), le flux est proportionnel ce gradient, et la constante de proportionnalit est appel e a constante de diffusion ($D$).
On obtient donc :
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
Cette quation est connue sous le nom de premi re loi de Fick.
(ID 16180)
Pour obtenir une expression du flux en un point et non une valeur moyenne on consid re la limite infinit simale des diff rentiels de flux. Dans ce cas, a densité de flux ($j$), en fonction de a constante de diffusion ($D$), ERROR:9080 et a distance ($\Delta z$), s crit comme suit :
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
Cette limite conduit la premi re loi de Fick, qui, dans sa forme continue et exprim e laide de a concentration ($c$) et a position ($z$), s crit comme suit :
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
(ID 16181)
Pour d terminer la concentration en un point, il est n cessaire de calculer les quantit s entrant et sortant dun volume de contr le. Ainsi, dans un espace d fini entre deux positions, on consid re le flux entrant moins le flux sortant. La variation de la quantit contenue est alors gale la concentration multipli e par la longueur du segment, ce qui quivaut au flux net multipli par lintervalle de temps consid r .
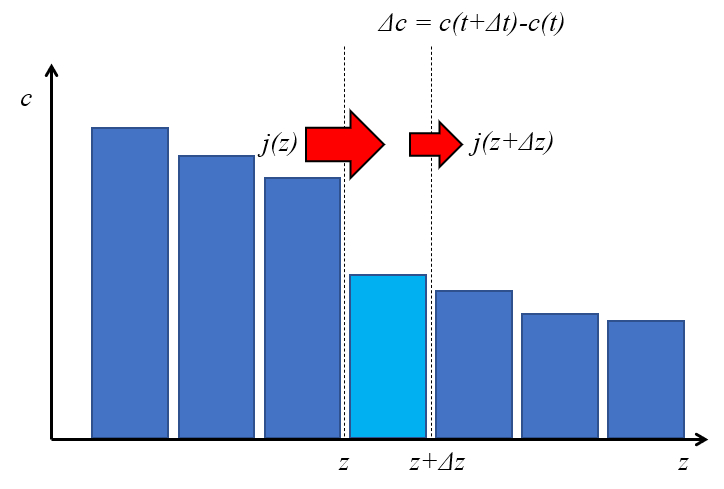
(ID 12141)
Si lon consid re un l ment de a distance ($\Delta z$) pendant un intervalle de temps a durée du temps ($\Delta t$), alors selon a densité de flux ($j$) :
• la position $z$, un flux de $j(z), \Delta t$ entre
• la position $z + \Delta z$, un flux de $j(z + \Delta z), \Delta t$ sort
Conform ment a variation de la densité de flux ($\Delta j$), la variation du contenu de l l ment est $\Delta c, \Delta z$.
Le bilan de masse sexprime donc comme suit :
$ \Delta c, \Delta z = \left[-j(z) + j(z + \Delta z)\right] \Delta t = -\Delta j, \Delta t $
Cela conduit la relation fondamentale suivante :
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
(ID 16182)
Pour obtenir la concentration en un point donn , il est n cessaire de passer de la version moyenn e la version locale. En utilisant a variation de la densité de flux ($\Delta j$), ERROR:9080, a distance ($\Delta z$) et a durée du temps ($\Delta t$), on part de l quation suivante :
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
En prenant la limite infinit simale, on obtient la forme diff rentielle correspondant la deuxi me loi de Fick. Celle-ci, exprim e laide de a densité de flux ($j$), a concentration ($c$), a position ($z$) et le temps ($t$), est donn e par :
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
(ID 16183)
Au XIXe si cle, plusieurs ph nom nes de transport taient d j connus, tels que la conduction thermique d crite par Fourier en 1822, lhydrodynamique des fluides d velopp e partir des quations de NavierStokes, ainsi que des processus biologiques comme losmose, dans lesquels le d placement de substances tait observ sans flux visible.

Adolf Fick (18291901) [1]
Adolf Fick remarqua que la diffusion de masse comme celle de loxyg ne dans les tissus semblait se comporter de mani re similaire la conduction thermique. En 1855, directement inspir par la loi de Fourier, Fick proposa une analogie pour la diffusion, formulant ce que lon conna t aujourdhui sous le nom de premi re loi de Fick, o le flux de masse est proportionnel au gradient de concentration. Cette loi lui permit de d crire le transport de sels ou de gaz travers des membranes semi-perm ables et des tissus biologiques. Par la suite, pour tudier l volution temporelle de la concentration, Fick combina cette loi avec le principe de conservation de la masse, donnant ainsi naissance ce que lon appelle aujourdhui la deuxi me loi de Fick, qui d crit l volution spatio-temporelle de la concentration dans un milieu diffusif. Il appliqua ces lois principalement lanalyse du transport de gaz dans les tissus, en particulier l tude de la diffusion de loxyg ne dans la corn e et des sels travers des membranes biologiques.[1] Adolf Fick (1829-1901) par le peintre Anton Klamroth[2] " ber Diffusion" (1855), publi dans les Annalen der Physik
(ID 16194)
La forme g n rale de la loi de Fick, impliquant a concentration ($c$), a constante de diffusion ($D$), a position ($z$) et le temps ($t$), s crit comme suit :
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
Lorsque le coefficient de diffusion a constante de diffusion ($D$) est constant, cette quation se simplifie en :
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
(ID 16185)
Dans le cas o a constante de diffusion ($D$) est constant, la loi g n rale de Fick se simplifie et permet dexprimer a concentration ($c$) en fonction de a position ($z$) et de le temps ($t$) :
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
En r solvant cette quation, on obtient lexpression analytique suivante :
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
(ID 16186)
La distribution obtenue pour a concentration ($c$), en fonction de a constante de diffusion ($D$), a position ($z$) et le temps ($t$), est donn e par :
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
Cette expression correspond une distribution de Gauss, illustr e ci-dessous :
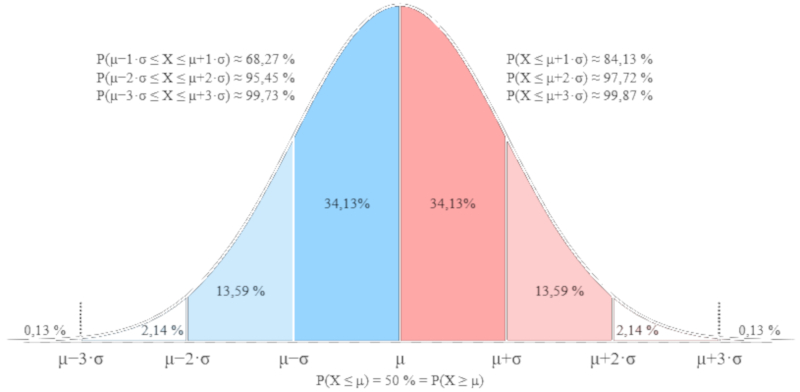
(ID 12142)
La largeur de la distribution est d termin e par le facteur a écart type ($\sigma$), qui correspond l cart type de la distribution et peut tre calcul e comme la racine carr e de a constante de diffusion ($D$) et le temps ($t$), selon :
| $ \sigma =\sqrt{2 D t }$ |
Cela signifie que la largeur augmente avec la racine carr e du temps, tandis que la hauteur maximale diminue proportionnellement linverse de ce facteur.
(ID 16188)
A concentration ($c$) repr sente une distribution d pendant de a constante de diffusion ($D$) et sexprime comme une fonction de a position ($z$) et le temps ($t$) :
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
Puisque le temps ($t$) est reli e a constante de diffusion ($D$) via a écart type ($\sigma$), on a :
| $ \sigma =\sqrt{2 D t }$ |
ce qui conduit :
| $ c =\displaystyle\frac{1}{\sqrt{2\pi} \sigma } e^{- z ^2/2 \sigma ^2 }$ |
(ID 16190)
A concentration ($c$) est influenc e par a vitesse du milieu ($u$), qui agit en opposition au processus de diffusion d crit par a constante de diffusion ($D$) dans la r gion positive de a position ($z$), modifiant ainsi la distribution de le temps ($t$) selon :
| $\displaystyle\frac{\partial c}{\partial t} + u \displaystyle\frac{\partial c}{\partial z} = D \displaystyle\frac{\partial^2 c}{\partial z ^2}$ |
Dans le cas o a vitesse du milieu ($u$) est constante, on obtient la solution suivante :
| $ c = c_0 [1 - erf\left(\displaystyle\frac{ z - u t }{ 2\sqrt{ D t }}\right)]$ |
o appara t la fonction erf, ou fonction derreur de Gauss :
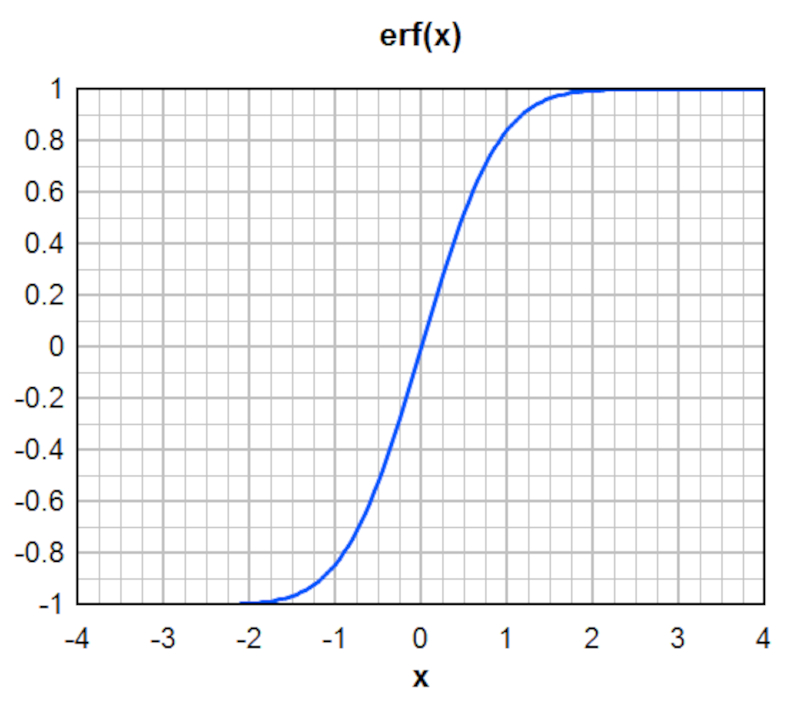
Cette solution implique que le point o la concentration atteint la moiti de sa valeur initiale se d place au cours du temps avec la vitesse d coulement, selon :
$z = u t$
Par ailleurs, le profil de concentration saplatit avec le temps, car la largeur de la zone de transition d pend de l cart type :
| $ \sigma =\sqrt{2 D t }$ |
(ID 16192)
(ID 16187)
ID:(1624, 0)
