Benützer:
Schallausbreitung
Storyboard 
Die Schallausbreitung im Ozean berücksichtigt sowohl die Reflexion an der Oberfläche und am Meeresboden als auch die Brechungen, die aufgrund von Druck-, Temperatur- und Salzgehaltsschwankungen auftreten.
ID:(1550, 0)
Interpretation der Schallbrechung
Konzept
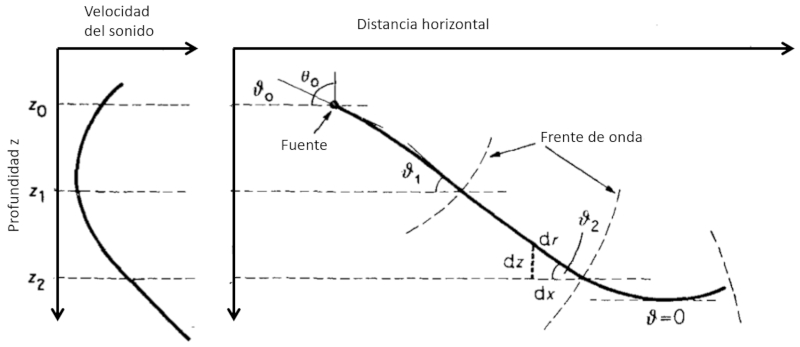
Wenn wir beobachten, wie sich der Klang mit der Tiefe und der Art seiner Ausbreitung ändert:
können wir sehen, dass:
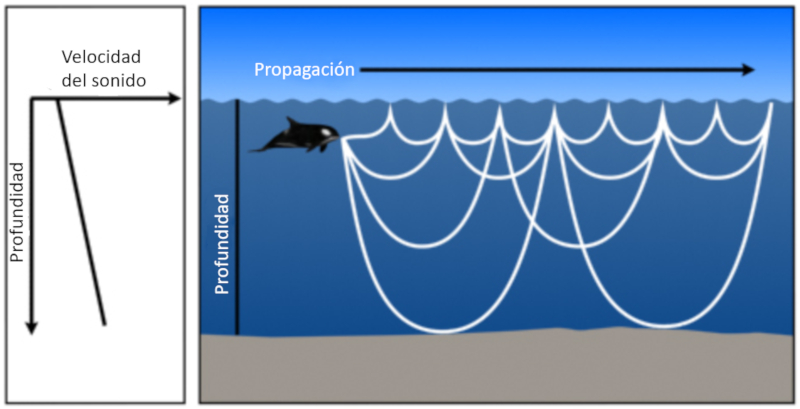
• Wenn die Schallgeschwindigkeit mit der Tiefe zunimmt, neigt der Winkel zwischen dem Strahl und dem Horizont dazu, sich zu verringern. Das bedeutet, dass der Klang dazu neigt, seinen Abstieg zu verringern, bis er horizontal wird und durch Symmetrie weiter zur Oberfläche aufsteigt.
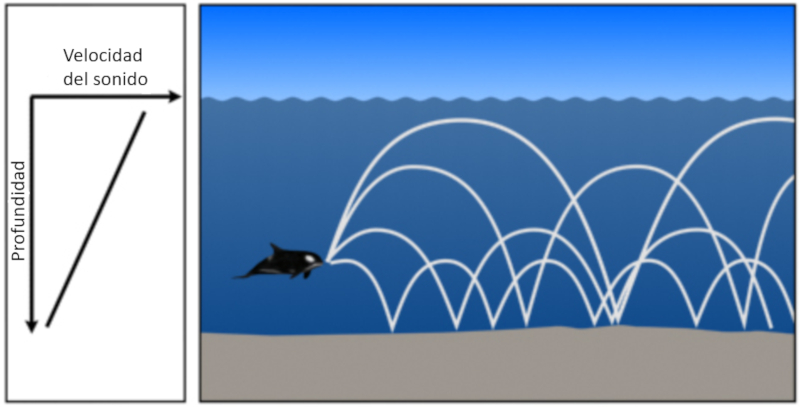
• Wenn die Schallgeschwindigkeit mit der Tiefe abnimmt, neigt der Winkel zwischen dem Strahl und dem Horizont dazu, sich zu vergrößern. Das bedeutet, dass der Klang dazu neigt, seinen Abstieg in Richtung des Bodens zu erhöhen.
ID:(11804, 0)
Wenn die Schallgeschwindigkeit zunimmt
Konzept
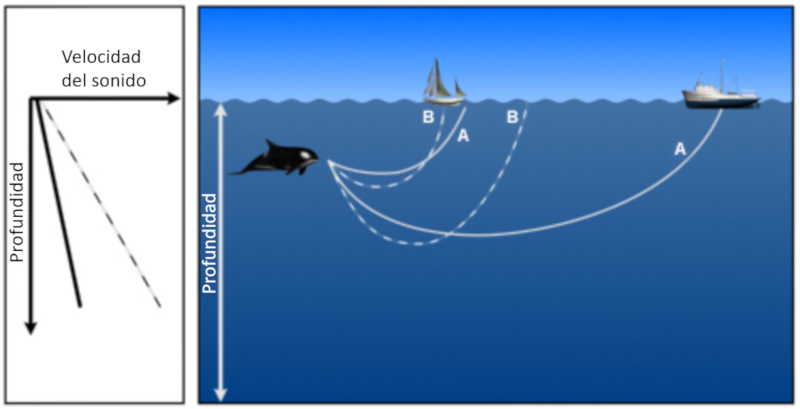
In einer Tiefe emittierter Schall, in der die Schallgeschwindigkeit mit der Tiefe zunimmt, kehren die Strahlen an die Oberfläche zurück, wo sie das Medium reflektieren und wieder durchdringen:
ID:(11805, 0)
Wenn die Schallgeschwindigkeit zunimmt und dann abnimmt
Konzept
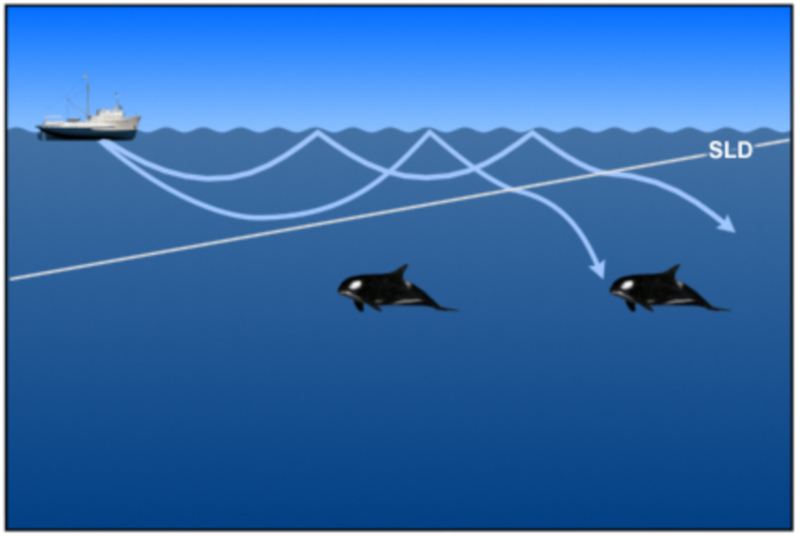
Schall, der in einer Tiefe abgegeben wird, in der die Schallgeschwindigkeit mit der Tiefe zunimmt, und die Strahlen an die Oberfläche zurückkehren. Wenn jedoch von einem Punkt aus die Schallgeschwindigkeit verringert wird, wird beobachtet, dass Strahlen mit einem größeren Winkel in Richtung der Tiefen gebrochen werden:
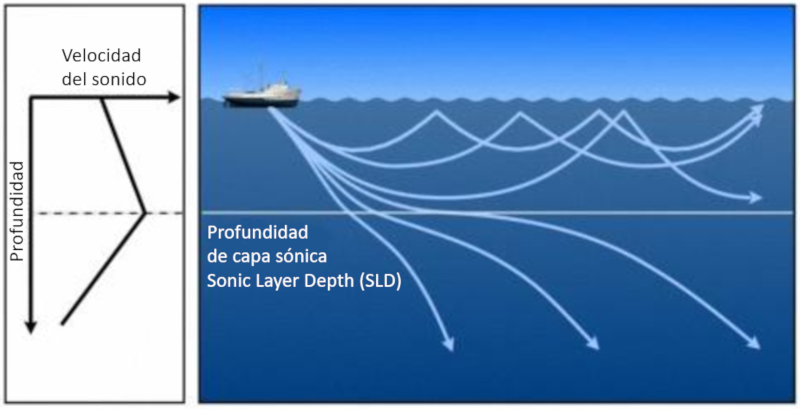
Somit wird ein Bereich gebildet, in dem die Strahlen zur Oberfläche zurückkehren. Diese Tiefe wird als SLD-Schallschichttiefe (Sonic Layer Depth) bezeichnet.
ID:(11806, 0)
Tonkanal
Konzept
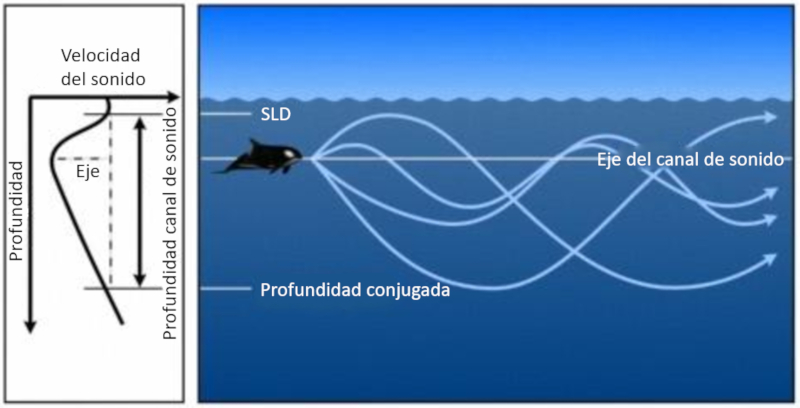
Wenn der Schall abnimmt und dann wieder zunimmt, entsteht eine Zone, in der er dazu neigt, zur Zone mit minimaler Geschwindigkeit zurückzukehren. Diese Zone wird als Schallkanal bezeichnet und erstreckt sich von der Tiefe der Schallgeschwindigkeitsschicht (SLD) bis zu einer konjugierten Tiefe:
Die Tiefe, in der die Schallgeschwindigkeit ein Minimum erreicht, wird als Schallkanalachse bezeichnet.
Es gibt sowohl Ausbreitung in der oberen Zone bis zur Tiefe der Schallgeschwindigkeitsschicht (SLD) als auch im Schallkanal. Die obere Zone hat jedoch das Problem, dass die Oberfläche den Schall dämpft, wodurch der Schallkanal am effektivsten wird.
ID:(11807, 0)
Schallverlust in der oberen Schicht
Konzept
Die Schallwellen, die sich über die Schallschichttiefe ausbreiten, können in die untere Zone gefiltert werden:
ID:(11808, 0)
Flacher Fall mit zunehmender Schallgeschwindigkeit
Konzept
Wenn das Wasser flach ist und die Schallgeschwindigkeit nur mit der Tiefe zunimmt, kehrt der Schall entweder durch Brechung oder Reflexion am Boden zur Oberfläche zurück, um dann von der Oberfläche reflektiert zu werden.:
ID:(11809, 0)
Flacher Fall mit reduzierter Schallgeschwindigkeit
Konzept
Wenn das Wasser flach ist und die Schallgeschwindigkeit nur mit der Tiefe abnimmt, tendiert der Schall dazu, nach unten zu gehen, wo er reflektiert wird:
ID:(11810, 0)
Schalltemperatur- und Geschwindigkeitsprofil
Konzept
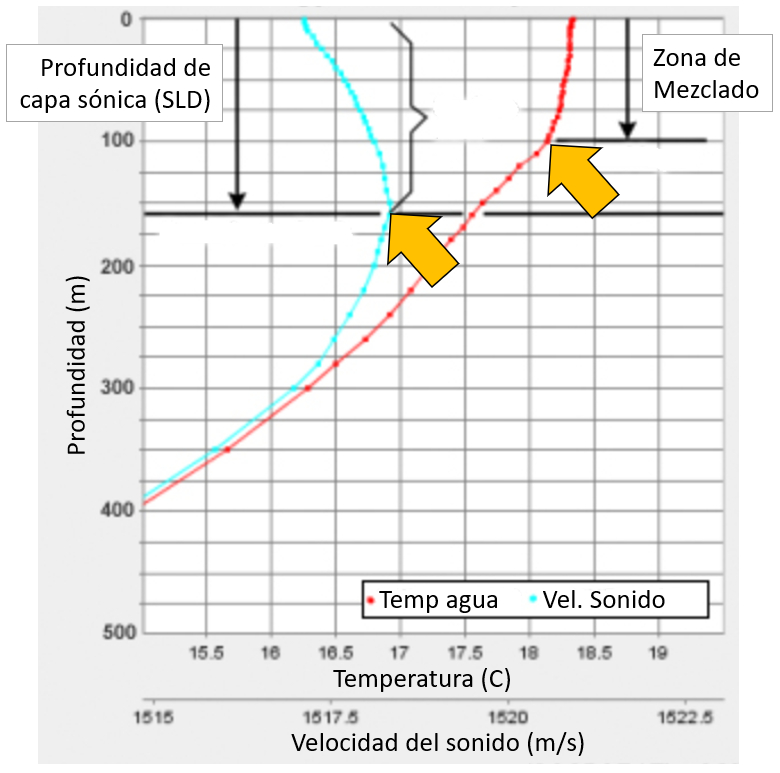
Die Temperatur durchläuft eine Zone, in der sie ungefähr konstant ist, bevor sie abfällt. Sie bleibt in der ersten Zone aufgrund der Turbulenzen, die vom Wind erzeugt werden und dazu neigen, das Wasser zu mischen, konstant.
Die Kurve der Schallgeschwindigkeit zeigt, dass sie ein Maximum erreicht, das die Tiefe der Schallgrenzschicht definiert. An ihrem maximalen Punkt wird die Tiefe der Schallgrenzschicht definiert:
ID:(11811, 0)
Verhalten in größerer Tiefe
Konzept
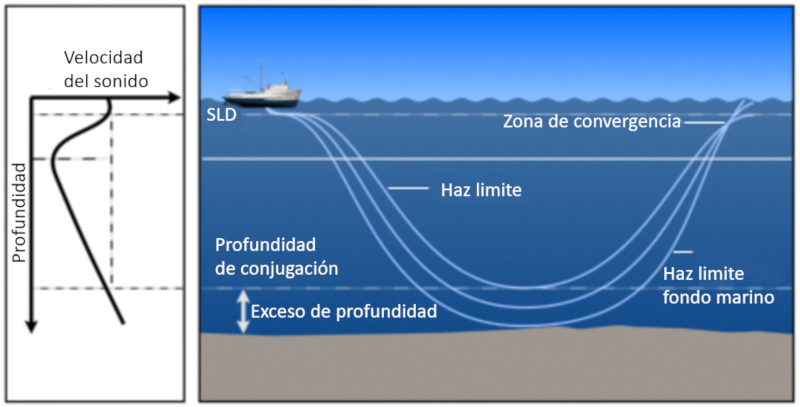
Im Allgemeinen steigt aufgrund der Schwerkraft die Schallgeschwindigkeit mit zunehmender Tiefe immer an. Wenn ein Schallstrahl die Tiefe der Schicht mit der Schallgeschwindigkeit (SLD) erreicht, divergiert er schließlich und kehrt zur Oberfläche zurück. Die Strahlen, die es schaffen, zur Oberfläche zurückzukehren, befinden sich zwischen einer Grenze, die durch die Reflexion am Boden definiert ist, und der Grenze des Strahls, der es schafft, in tiefere Schichten einzudringen und schließlich die Oberfläche zu erreichen:
ID:(11812, 0)
Ausbreitung über größere Entfernungen
Konzept
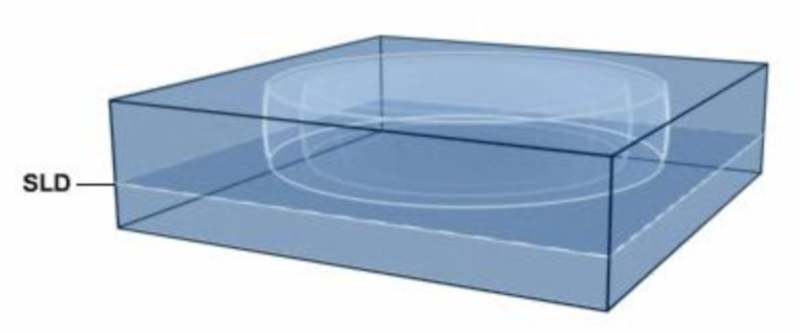
Für Schall, der nahe der Oberfläche abgestrahlt wird, kann die Ausbreitung als sphärische Ausbreitung modelliert werden. Hochfrequenter Schall neigt dazu, sich auf größere Entfernungen zu dämpfen, weshalb das sphärische Modell ausreicht. Für Schall mit niedriger Frequenz kann er jedoch durch das gesamte Becken reisen. In diesem Fall bewegt er sich durch den oberen Bereich bis zur Tiefe der akustischen Schicht (SLD) und/oder durch den Schallkanal. In beiden Fällen kann das System mit zylindrischen Koordinaten modelliert werden:
ID:(11813, 0)
Echtes Schallprofil
Konzept
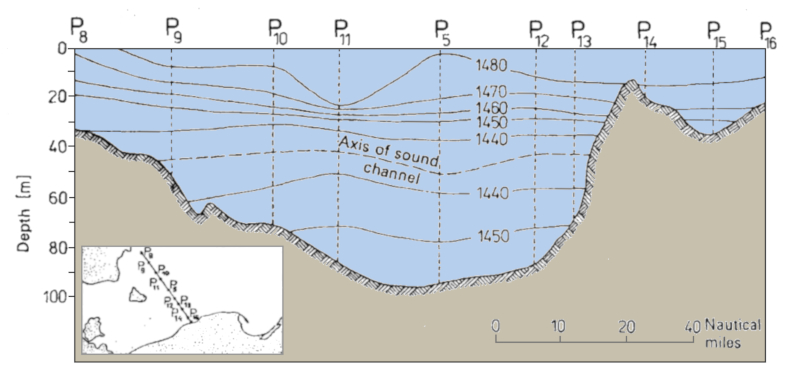
Ein Profil einer Region, wie zum Beispiel eines Kanals, kann erstellt werden, indem die Geschwindigkeiten für jede Tiefe dargestellt werden. Dadurch können Schallkanäle und die Tiefe der Schicht des Schalls erkannt werden:
ID:(11826, 0)
Modell
Top
Berechnungen
Variablen
Parameter
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden Gleichung
$ I =\displaystyle\frac{ P }{ 2 \pi r h }$
I = P /(2* pi * r * h )
$\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$
sin( theta_i )/sin( theta_r )= c_i / c_e
$\displaystyle\frac{ d\vartheta }{ dz }=-\displaystyle\frac{\tan \vartheta }{ c } \displaystyle\frac{ dc }{ dz }$
diff( vartheta , z )=-tan( vartheta )*diff( c , z )/ c
ID:(15466, 0)
Ley de Snell en función de la velocidad
Gleichung
La relación entre los ángulos de incidencia y refractados indicados en la siguiente gráfica
se pueden escribir en función de la velocidad de la luz en cada medio
| $\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
Observando la imagen se nota que los senos de los angulos son respectivamente\\n\\n
$\sin\theta_i=\displaystyle\frac{c_i\Delta t}{d}$
y\\n\\n
$\sin\theta_e=\displaystyle\frac{c_e\Delta t}{d}$
\\n\\nSi se despeja en ambas ecuaciones la distancia
$d=\displaystyle\frac{c_i\Delta t}{\sin\theta_i}=\displaystyle\frac{c_e\Delta t}{\sin\theta_e}$
por lo que se tiene que
| $\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
ID:(3342, 0)
Schallbrechung
Gleichung
Die Brechung von Schall beim Übergang von einem Medium in ein anderes wird im Allgemeinen durch das Snelliussche Gesetz beschrieben:
$\displaystyle\frac{\sin\theta_2}{\sin\theta_1}=\displaystyle\frac{c_2}{c_1}$
wobei $\theta$ der Einfallswinkel zwischen der Normalen zur Oberfläche und dem Strahl ist, und $c$ die Schallgeschwindigkeiten in den Medien 1 und 2 sind. Im Fall eines Strahls, der durch das Wasser des Ozeans propagiert, ändern sich die Geschwindigkeiten allmählich. Andererseits ist es praktisch, mit einem Winkel $\vartheta$ des Strahls zur Horizontalen zu arbeiten. Daher kann das Gesetz umgeschrieben werden, indem man das Sinus des Winkels $\theta$ durch den Kosinus des komplementären Winkels $\vartheta$ ersetzt. Wenn wir eine kleine Variation des Winkels und der Geschwindigkeit betrachten, wenn sich die Tiefe um $dz$ erhöht, erhalten wir:
$\displaystyle\frac{\cos(\vartheta + d\vartheta)}{\cos\vartheta}\sim 1-\tan\vartheta d\vartheta = 1+\displaystyle\frac{dc}{c}$
daher ist die Beziehung für die Tiefenvariation:
| $\displaystyle\frac{ d\vartheta }{ dz }=-\displaystyle\frac{\tan \vartheta }{ c } \displaystyle\frac{ dc }{ dz }$ |
ID:(11803, 0)
Schallausbreitung im Schallkanal
Gleichung
Mientras que en el espacio el sonido se propaga en todas las direcciones reduciéndose la intensidad con la distancia al inverso del radio al cuadrado con
| $ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ W }{ r ^2}$ |
dentro del canal sónico lo hace en un sistema bidimensional con lo que la intensidad se reduce con la distancia a la inversa con :
| $ I =\displaystyle\frac{ P }{ 2 \pi r h }$ |
ID:(11878, 0)